Тема уроку. Перпендикулярність прямої і площини. Ознака перпендику-лярності прямої і площини.

Мета уроку: формування поняття прямої, перпендикулярної до площини. Вивчення ознаки перпендикулярності прямої і площини.

Обладнання: стереометричний набір, модель куба.

Хід уроку

І. Перевірка домашнього завдання

1. Відповіді на запитання, які виникли в учнів при виконанні домаш­нього завдання.

2. Самостійна робота.

Варіант 1

1) Промені 0В, ОС, OD попарно перпендикулярні. Знайдіть довжину відрізка ВС, якщо OD = а, DC = b, DB = с . (6 балів)

2) Дано прямокутний паралелепіпед ABCDA₁B₁C₁D₁. Доведіть, що АС СС₁. (6 балів)

Варіант 2

1) Промені 0В, ОС, OD попарно перпендикулярні. Знайдіть довжину відрізка ОС, якщо BD = а , DC = b, OB = с . (6 балів)

2) Дано прямокутний паралелепіпед АВСDА₁В₁С₁D₁. Доведіть, що АВ В₁С₁. (6 балів)

Варіант 3

1) У прямокутному паралелепіпеді ABCDA₁B₁C₁D₁ АВ = b, А₁В = а, AD = с. Знайдіть A₁D . (6 балів)

2) У трикутній піраміді SABC, всі ребра якої рівні, точки М і N — се­редини ребер АС і SB відповідно. Доведіть, що MN AC. (6 балів)

Варіант 4

1) У прямокутному паралелепіпеді АВСDА₁В₁С₁D₁  BD = с, ВА₁= а , AD = b. Знайдіть ребро АА₁. (6 балів)

2) У трикутній піраміді SABC, всі ребра якої рівні, точки М і N — се­редини ребер AS і ВС відповідно. Доведіть, що MN AS . (6 балів)

Відповідь.  Варіант 1. 1) . Варіант 2. 1) .

Варіант 3. 1) . Варіант 4. 1) .

II. Сприйняття й усвідомлення нового матеріалу

Означення перпендикулярності прямої і площини

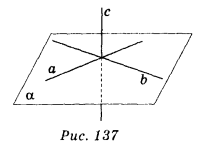Уявлення про пряму перпендикулярну до площини дають вертика­льно поставлені стовпи — вони перпендикулярні до поверхні землі, пер­пендикулярні до будь-якої прямої, яка проходить через основу стовпа і лежить у площині землі.

Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину та перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.

На рис. 137 пряма с перпендикулярна до площини α. Пишуть: с α. З означення ви­пливає, що с a , с b.

Розв'язування задач

1. Укажіть в оточуючому просторі моделі прямих і площин, які перпендику-лярні.
2. Чи правильно, що коли пряма не перпендикулярна до площини, то вона не перпендикулярна ні до жодної прямої, яка лежить в цій площині?
3. Що означає твердження: пряма не перпендикулярна до площини?
4. Пряма SA перпендикулярна до площини прямокутника ABCD. Укажіть перпендикулярні прямі (рис. 138).

(Відповідь. SA AB; SA AC ; SA AD.)

Ознака перпендикулярності прямої і площини

Як перевірити, чи перпендикулярна дана пряма до даної площини? Це питання має практичне значення, наприклад, при установці щогл, колон тощо, які потрібно поставити прямо, тобто перпендикулярно до площини землі. Насправді немає необхідності перевіряти перпендику­лярність прямої до всіх прямих, що лежать у даній площині й прохо­дять через точку перетину даної прямої і площини, а досить перевірити перпендикулярність лише до двох прямих, які лежать у площині і про­ходять через точку перетину прямої і площини. Це випливає з теореми, що виражає ознаку перпендикулярності прямої і площини.

Теорема.

Якщо пряма перпендикулярна до двох прямих, які лежать у площині й перетинаються, то вона перпендикулярна до даної площини.

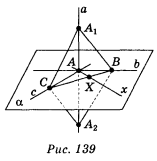Далі колективно розбирається доведення сформульованої теореми за заготовленим рисунком і умовою теореми.

Наводимо запис, що робиться на дошці і в зошитах учнів.

Дано:

a с, a b, b α, с α; а, b, с перетинаються в точці А; х α .

Довести: а х (рис. 139).

Доведення

Додаткові побудови: проводимо пряму в площині α, яка перетинає прямі b, х, с в точках В, X, С, та відкладаємо на прямій а АА₁ = АА₂.

Розв'язування задач

1. Дано зображення куба ABCDA₁B₁C₁D₁. Довести, що:

а)АА₁ (АВС);      б) AD (DCC₁);      в) B₁D₁ (A₁C₁C);                 

г) А₁В₁ ВС₁;       д) ΔAB₁C₁ — прямокутний;      е) AB₁C₁D — прямокутник.

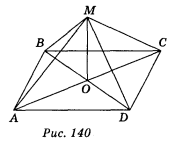2. Дано: ABCD — паралелограм; МА = МС, MB = MD. До вест й, що  

МО  (АВС) (рис. 140).

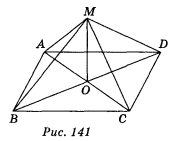
3. Дано: ABCD — квадрат; MB = MD (рис. 141). Довести, що BD (MAO).

4. Задача № 6 із підручника (с. 34).

III. Домашнє завдання

§ 3, п. 15; контрольні запитання № 3, 4; задача № 7 (с. .34).

IV. Підведення підсумку уроку

Запитання до класу

1) Сформулюйте означення прямої, перпендикулярної до площини.

2) Сформулюйте ознаку перпендикулярності прямої і площини.

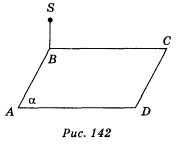3) Точка S лежить поза площиною ромба ABCD, причому SB BC , SB AB , <BAD = 60° (рис. 142). Які з наведених тверджень пра­вильні, а які — неправильні:

а) пряма SB перпендикулярна до площини АВС;

б) пряма AB перпендикулярна до прямої SB;

в) пряма BC перпендикулярна до площини ASB;

г) пряма SB перпендикулярна до прямої BD ?

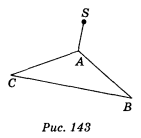4) Точка S лежить поза площиною трикутника АВС, причому SAAC, ABAC, SA = SB = AB (рис. 143). Які з наведених тверджень пра­вильні, а які — неправильні:

а) пряма SA не перпендикулярна до площини АВС;

б) пряма AB перпендикулярна до площини SAC;

в) пряма АС перпендикулярна до площини SAB;

г) пряма BC перпендикулярна до площини ASC?