Властивості прямої і площини, перпендикулярних між собою.
Тема уроку. Властивості прямої і площини, перпендикулярних між собою.
Мета уроку: формування знань учнів про властивості перпендикулярних прямих і площин.
Обладнання: стереометричний набір, схема «Властивості прямо і площини, перпендикулярних між собою» (с. 116).
Хід уроку
І. Перевірка домашнього завдання
- Колективне обговорення розв'язування задачі № 10.
- Математичний диктант.
Дано зображення куба: варіант 1 — рис. 151, варіант 2 — рис. 152.


Користуючись зображенням, запишіть:
- площину, яка проходить через точку М прямої AM і перпендикулярна до неї; (2 бали)
- пряму, яка перпендикулярна до площини АВС і проходить через точку D; (2 бали)
- пряму, яка перпендикулярна до площини АВС і проходить через точку N; (2 бали)
- площину, яка перпендикулярна до прямої BD; (2 бали)
- прямі, які перпендикулярні до площини АМС; (2 бали)
- площини, які перпендикулярні до прямої DC. (2 бали)
Відповідь.
Варіант 1. 1) (MNK); 2) KD; 3) BN; 4) (ACМ); 5) BD і KN; 6) (ADK) і (BCL).
Варіант 2. 1) (MNK); 2) DL; 3) CN; 4) (АСМ); 5) BD i KL; 6) (BCN) і (ADM).
II. Сприйняття й усвідомлення нового матеріалу
Властивості прямої і площини, перпендикулярних між собою
 Теорема 1.
Теорема 1.
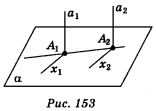
Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.
Доведення
Нехай а1 || а2 і a1 ![]() α. Доведемо, що α
α. Доведемо, що α ![]() а2 (рис. 153). Точки А1 і А2 — точки перетину а1 і а2 з площиною α.
а2 (рис. 153). Точки А1 і А2 — точки перетину а1 і а2 з площиною α.
У площині α через точку А2 проведемо довільну пряму х2, а через точку А1 — пряму х1 таку, що х1 || х2. Оскільки a1 || а2, x1 || х2 і а1 ![]() х1, то за теоремою 3.1 а2
х1, то за теоремою 3.1 а2 ![]() х2. Оскільки х2 вибрана довільно в площині α, то а2
х2. Оскільки х2 вибрана довільно в площині α, то а2 ![]() α.
α.
Теорема 2.
 Якщо дві прямі перпендикулярні до однієї і тієї самої площини, то дані прямі паралельні.
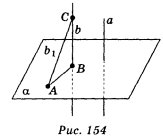
Якщо дві прямі перпендикулярні до однієї і тієї самої площини, то дані прямі паралельні.
Доведення
 Нехай a
Нехай a ![]() α , b
α , b ![]() α . Доведемо, що а || b (рис. 154). Припустимо, що а
α . Доведемо, що а || b (рис. 154). Припустимо, що а![]() b. Тоді через точку С прямої b проведемо b1 , паралельну а. Оскільки а
b. Тоді через точку С прямої b проведемо b1 , паралельну а. Оскільки а ![]() α , то і b1
α , то і b1 ![]() α за доведеною теоремою, а за умовою b
α за доведеною теоремою, а за умовою b ![]() α. Якщо точки А і В — точки перетину прямих b1 і b з площиною α, то з припущення випливає, що в трикутнику <A = <В = 90° , що не може бути. Отже, а || b.
α. Якщо точки А і В — точки перетину прямих b1 і b з площиною α, то з припущення випливає, що в трикутнику <A = <В = 90° , що не може бути. Отже, а || b.
Розв'язування задач
1. Визначте вид чотирикутника AA1B1B якщо:
а) АА1 ![]() α; АА1 || ВВ1; А
α; АА1 || ВВ1; А ![]() α, В
α, В ![]() α; AA1 ≠ ВВ1 (рис. 155);
α; AA1 ≠ ВВ1 (рис. 155);
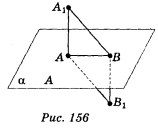
б) АА1 ![]() α; ВВ1
α; ВВ1 ![]() α; А
α; А ![]() α, В
α, В ![]() α (рис. 156);
α (рис. 156);
 в) А
в) А ![]() α; В
α; В ![]() α; АА1
α; АА1 ![]() α; ВВ1
α; ВВ1 ![]() α; АА1 = ВВ1 (рис. 156).
α; АА1 = ВВ1 (рис. 156).
2. Задача № 12 із підручника (с. 35).
3. Задача № 13 із підручника (с. 35).
4. Задача № 16 із підручника (с. 35).
Теорема 3.
Якщо пряма перпендикулярна до однієї із двох паралельних площин, то вона перпендикулярна і до другої.
 Доведення
Доведення
Нехай α || β , а ![]() α. Доведемо, що α
α. Доведемо, що α ![]() β. (рис. 157). Нехай точки А і В — точки перетину прямої а з площинами α і β. В площині β проведемо через точку В довільну пряму b. Через пряму b і точку А проведемо площину γ, яка перетинає α по прямій с, причому с || b. Оскільки а
β. (рис. 157). Нехай точки А і В — точки перетину прямої а з площинами α і β. В площині β проведемо через точку В довільну пряму b. Через пряму b і точку А проведемо площину γ, яка перетинає α по прямій с, причому с || b. Оскільки а ![]() α , то а
α , то а ![]() с (за означенням прямої, перпендикулярної до площини). Оскільки а
с (за означенням прямої, перпендикулярної до площини). Оскільки а ![]() с, b || с і а, b, с лежать в γ, то а
с, b || с і а, b, с лежать в γ, то а ![]() b. Враховуючи, що b — довільна пряма площини β, маємо а
b. Враховуючи, що b — довільна пряма площини β, маємо а ![]() β.
β.
Теорема 4.
 Якщо дві площини, перпендикулярні до однієї і тієї самої прямої, то вони паралельні.
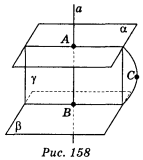
Якщо дві площини, перпендикулярні до однієї і тієї самої прямої, то вони паралельні.
Доведення
Нехай α ![]() а, β
а, β ![]() а, доведемо, що α || β (рис. 158). Нехай точки А і В — точки перетину прямої а з площинами α і β. Припустимо, що α
а, доведемо, що α || β (рис. 158). Нехай точки А і В — точки перетину прямої а з площинами α і β. Припустимо, що α ![]() β. Візьмемо точку С на прямій перетину площин α і β. С
β. Візьмемо точку С на прямій перетину площин α і β. С ![]() а, бо в противному випадку через точку С проходили б дві різні площини α і β, перпендикулярні до прямої а, що неможливо. Проведемо площину γ через точку С і пряму а, ця площина перетинає α і β по прямих АС і ВС відповідно. Оскільки а
а, бо в противному випадку через точку С проходили б дві різні площини α і β, перпендикулярні до прямої а, що неможливо. Проведемо площину γ через точку С і пряму а, ця площина перетинає α і β по прямих АС і ВС відповідно. Оскільки а ![]() α, то а
α, то а ![]() АС, аналогічно а
АС, аналогічно а ![]() ВС. Отже, в площині γ через точку С проходять дві різні прямі АС і ВС, які перпендикулярні до прямої а, що неможливо. Отже, α || β.
ВС. Отже, в площині γ через точку С проходять дві різні прямі АС і ВС, які перпендикулярні до прямої а, що неможливо. Отже, α || β.
Розв'язування задач
-
Нехай ABCD – прямокутник, BS
 АВ , AM
АВ , AM  АВ (рис. 159). Як розташовані площини AMD і BSC?
АВ (рис. 159). Як розташовані площини AMD і BSC?
-
В1
 β; АА1
β; АА1  α, АА1
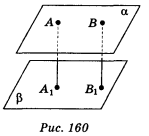
α, АА1  β; BВ1 || АА1; АА1 = 12 cm, A1B = 13 см (рис. 160). Знайти АВ.
β; BВ1 || АА1; АА1 = 12 cm, A1B = 13 см (рис. 160). Знайти АВ.
-
А1
 α. В1
α. В1  α, А2
α, А2  β, В2
β, В2  β, AA1
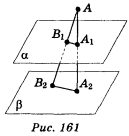
β, AA1  α; α || β (рис. 161). Визначте вид трикутників AA1B1 і АА2В2.
α; α || β (рис. 161). Визначте вид трикутників AA1B1 і АА2В2.

III. Домашнє завдання
§ 3, п. 17; контрольні запитання № 5, 6; задачі № 14, 15 (с. 35).
IV. Підведення підсумку уроку
При підведенні підсумку уроку можна скористатися даною схемою.
Властивості прямої і площини, перпендикулярних між собою |
||
|
|
Дано: а || b,
a Довести:
b |
Дано:
a
b Довести: а || b. |
|
|
Дано: α || β,
а
Довести: β |
Дано:
α
β Довести: α || β. |
Запитання до класу
- Як розташовані прямі, які перпендикулярні до площини?
- Як розташовані в просторі площини, які перпендикулярні до прямої?
- Як розташовані пряма і площина, якщо паралельна пряма до даної прямої перпендикулярна до площини?
- Як розташовані пряма і площина, якщо площина, паралельна до даної площини, перпендикулярна до даної прямої?


про публікацію авторської розробки
Додати розробку


