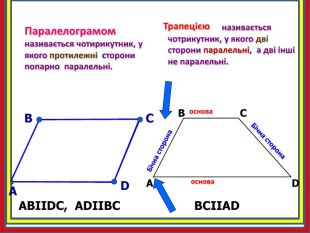
Площа трапеції. презентація

ПлощатрапеціїЧеркаси, СШ № 28, Леонова Валентина Леонтіївна8 клас

Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. Вона виховує волю, характер. В. О. Сухомлинський. Український  педагог, публіцист, письменник,  поет, Заслужений вчитель УРСР. Кандидат педагогічних наук  (1955)

Повторимо!1. Яку фігуру називають трапецією? 2. Сформулюйте властивості трапеції. 4. Сформулюйте властивості рівнобічної трапеції. 3. Які види трапеції ви знаєте?Рівнобічна. Прямокутна5. Що називають середньою лінією трапеції?

AВСDосноваоснова. Бічна сторона. Бічна сторона називається чотрикутник, у якого дві сторони паралельні, а дві інші не паралельні. ВАСDАВIIDС, ADIIBC ВСIIАD Трапецією. Паралелограмом називається чотирикутник, у якого протилежні сторони попарно паралельні.

Повторимо!1. Яку фігуру називають трапецією? 2. Сформулюйте властивості трапеції. 4. Сформулюйте властивості рівнобічної трапеції. 3. Які види трапеції ви знаєте?Рівнобічна. Прямокутна5. Що називають середньою лінією трапеції?

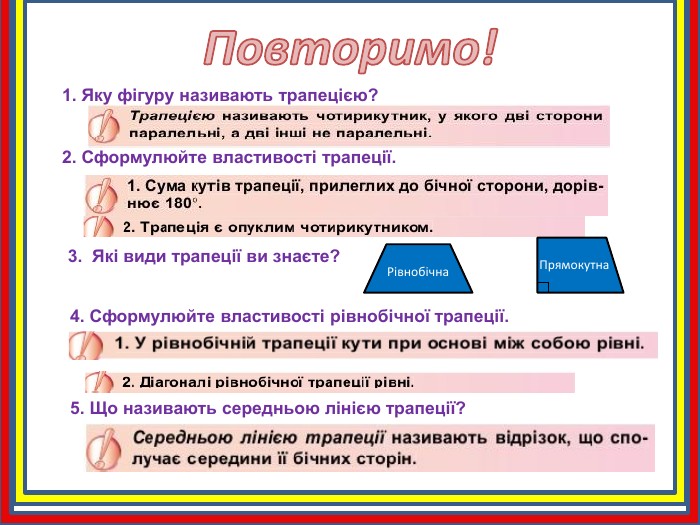
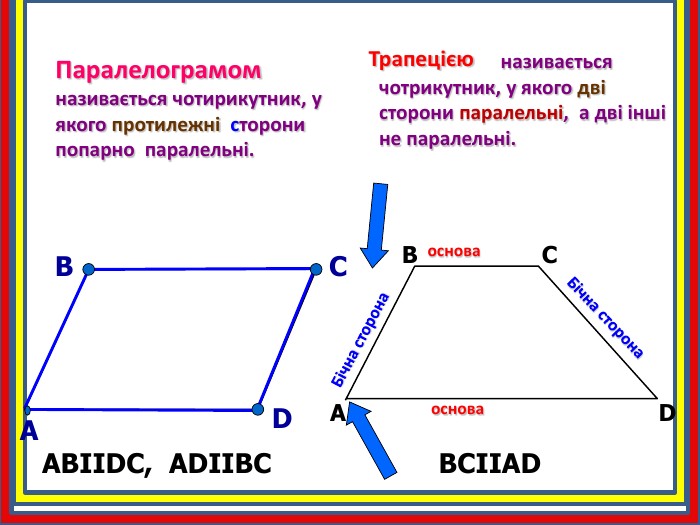
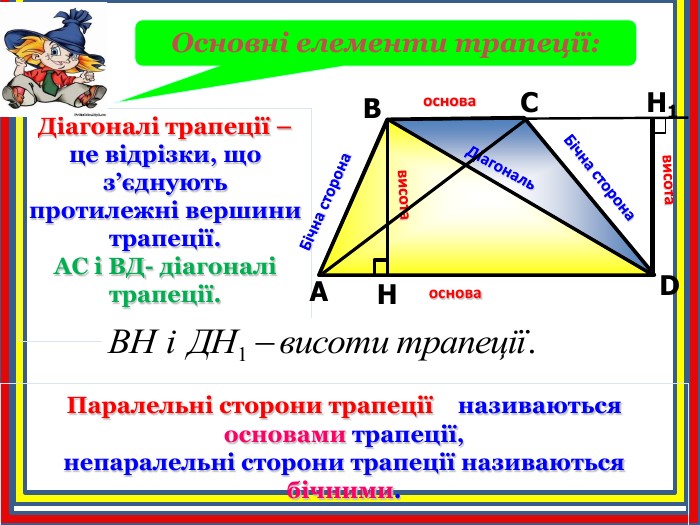
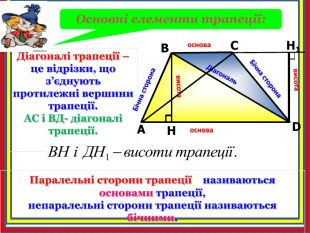
Діагоналі трапеції – це відрізки, що з’єднують протилежні вершини трапеції. АС і ВД- діагоналі трапеції. АСDВH1 Основні елементи трапеції: Бічна сторона. Бічна сторонаосноваоснова. Hвисотависота. Діагональ. Паралельні сторони трапеції називаються основами трапеції, непаралельні сторони трапеції називаються бічними.

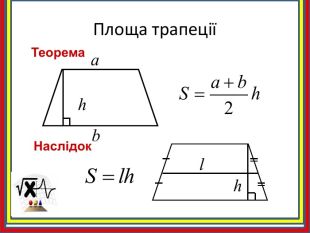
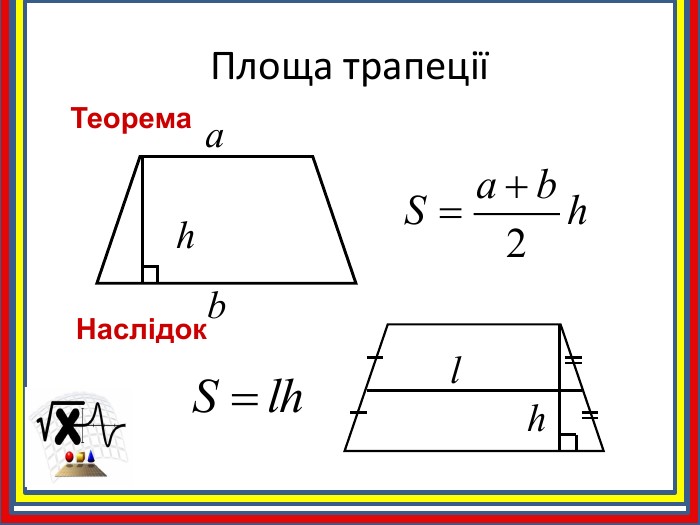
Площа трапеції Теорема (про площу трапеції)Площа трапеції дорівнює добутку півсуми її основ на висоту. Доведення: АBCDKNНехай ABCD – довільна трапеція з основами BC і AD, BK- її висота. Доведемо, що площу трапеції S можна знайти за формулою 𝑆=𝐴𝐷+𝐵𝐶2∙𝐵𝐾. Діагональ BD розбиває трапецію на два Трикутники ABD і BDC. Тому 𝑆=12∙ 𝑆𝐴𝐵𝐷+𝑆𝐵𝐷𝐶.2) BK- висота ∆ ABD, тому 𝑆𝐴𝐵𝐷=12∙𝐴𝐷∙𝐵𝐾. 3) Проведемо у трапеції висоту DN, вона є і висотою ∆ BDC, тому 𝑆𝐵𝐷𝐶=12∙𝐵𝐶∙𝐷𝑁.4) DN=BK (як висоти трапеції). Отже 𝑆=12∙ 𝑆𝐴𝐵𝐷+𝑆𝐵𝐷𝐶= 12∙𝐴𝐷∙𝐵𝐾+ 12∙𝐵𝐶∙𝐷𝑁== 𝐴𝐷+𝐵𝐶2 ∙ BK.  S =𝒂+𝒃𝟐∙ h a і b – основи трапеції, h – висота трапеціїS =с.л∙ h 

Площа трапеції: S =𝒂+𝒃𝟐∙ ha і b – основи трапеції, h – висота трапеції 

Площа трапеції: S =𝒂+𝒃𝟐∙ ha і b – основи трапеції, h – висота трапеції 

Діагоналі трапеції – це відрізки, що з’єднують протилежні вершини трапеції. АС і ВД- діагоналі трапеції. АСDВH1 Основні елементи трапеції: Бічна сторона. Бічна сторонаосноваоснова. Hвисотависота. Діагональ. Паралельні сторони трапеції називаються основами трапеції, непаралельні сторони трапеції називаються бічними.

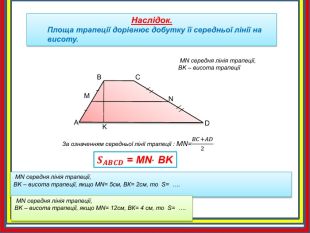
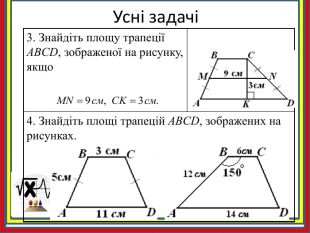
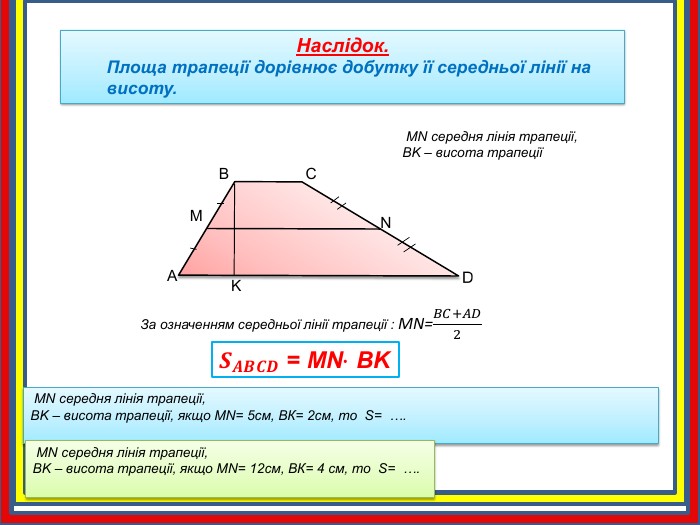
Наслідок. Площа трапеції дорівнює добутку її середньої лінії на висоту. АBCMNKЗа означенням середньої лінії трапеції : MN=𝐵𝐶+𝐴𝐷2  𝑺𝑨𝑩𝑪𝑫 = MN∙ BK  MN середня лінія трапеції,BK – висота трапеції MN середня лінія трапеції,BK – висота трапеції, якщо МN= 5cм, ВК= 2см, то S= …. MN середня лінія трапеції,BK – висота трапеції, якщо МN= 12cм, ВК= 4 см, то S= ….

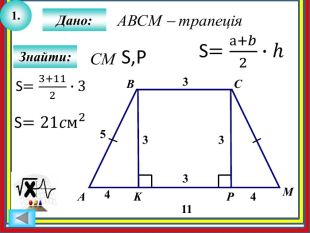
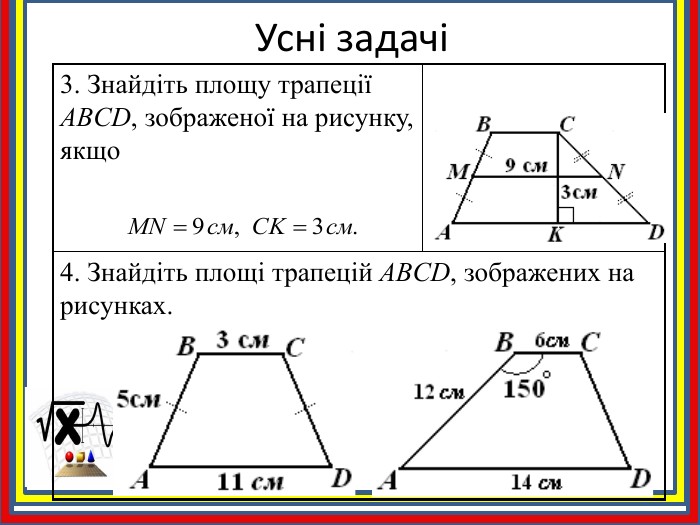
1. Знайдіть площу трапеції, якщо її середня лінія дорівнює 4 см, а висота - 5 см. Наслідок. Площа трапеції дорівнює добутку її середньої лінії на висоту. 𝑺𝑨𝑩𝑪𝑫 = MN∙ BK Де MN середня лінія трапеції, BK – висота трапеції𝑺𝑨𝑩𝑪𝑫 = 4∙ 5 2 Висота трапеції дорівнює 3 см, а середня лінія - 6 см. Знайдіть площу трапеції.𝑺𝑨𝑩𝑪𝑫 = 3∙ 6 2 Висота трапеції дорівнює 10 см, а середня лінія - 6 см. Знайдіть площу трапеції.𝑺𝑨𝑩𝑪𝑫 = 10∙ 6 

Площа трапеції Якщо задано діагоналі трапеції та кут між ними (див. рис.),то площу трапеції знаходять через половину добутку діагоналей трапеції на синус кута між ними. Варто зазначити, що неважливо чи тупий чи гострий кут підставляємо у формулу. Значення площі від цього не поміняється. АBCD𝑑1 𝑑2 αβS = 12𝑑1𝑑2sin𝛼 S = 12𝑑1𝑑2sinβ S = 12𝑑1𝑑2sin𝛼 

Площа трапеції : S = 12𝑑1𝑑2sinβ 

Площа трапеції : S = 12𝑑1𝑑2sinβ 

1. Знайти: K3 Дано: АBCMP11 4 4 5 S,РS=а+𝑏2∙h S=3+112∙3 3 3 3 S=21𝑐м2 

2. Знайти: АBCD8??450 КS=а+𝑏2∙h У∆АВК(∠К=900) : АВ2=АК2+ВК2 АВ2=82+82 АВ2=128 𝐴В=128 𝐴В=82 За власт. кола, вписаного в трапецію: АВ+СD=BC+AD, тому. АВ+СD=BC+AD, тому. BC+AD=8+82 S=32+322 S=8+822∙8 

3. Дано: Знайти: АBCD

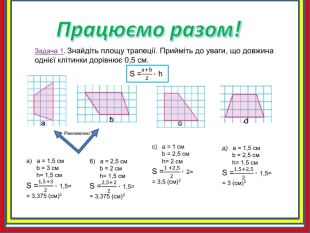
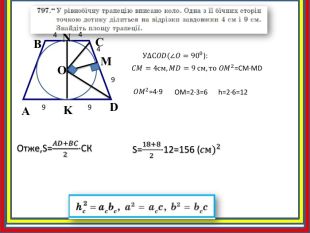
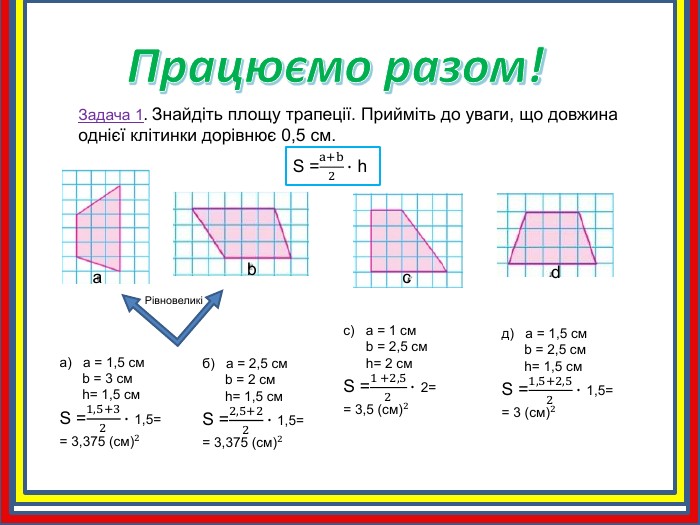
Працюємо разом!Задача 1. Знайдіть площу трапеції. Прийміть до уваги, що довжина однієї клітинки дорівнює 0,5 cм. abcd. S =a+b2∙ h с) a = 1 см b = 2,5 см h= 2 см. S =1 +2,52∙ 2== 3,5 (см)2 б) a = 2,5 см b = 2 см h= 1,5 см. S =2,5+22∙ 1,5== 3,375 (см)2 а) a = 1,5 см b = 3 см h= 1,5 см. S =1,5+32∙ 1,5== 3,375 (см)2 д) a = 1,5 см b = 2,5 см h= 1,5 см. S =1,5+2,52∙ 1,5== 3 (см)2 Рівновеликі

Площа трапеції: S =𝒂+𝒃𝟐∙ ha і b – основи трапеції, h – висота трапеції Основи трапеції дорівнюють 7 см і 13 см, а її площа - 40 см2. Знайдіть висоту трапеції.

Задача. Актова зала школи має форму трапеції з основами 20 м і 10 м та висотою 8 м. Чи вистачить 9 кг фарби, щоб пофарбувати підлогу актової зали, якщо витрати фарби становлять 1 кг/10 м2?Розв'язання до задачі:𝑆=1220+10∙8=120 (м2)120 : 10 =12 (кг) – фарби потрібно для пофарбування підлоги актової зали. Відповідь. Не вистачить 9 кг фарби для пофарбування підлоги. 

Площа трапеціїhab. Теорема. Наслідокlh

Усні задачі1. На папері у клітинку зображено трапецію АВСD, вершини якої збігаються з вершинами клітинок (див. рисунок). Знайдіть площу трапеції АВСD, якщо кожна клітинка є квадратом зі стороною завдовжки 1 см. 2. Знайдіть площу трапеції ABCD, зображеної на рисунку.

Усні задачі3. Знайдіть площу трапеції ABCD, зображеної на рисунку, якщо 4. Знайдіть площі трапецій ABCD, зображених на рисунках.

АDСВKMNO49 У∆С𝑂𝐷(∠𝑂=900):  𝐶𝑀=4см, 𝑀𝐷=9 см, то 𝑂𝑀2=CM∙MD   𝑂𝑀2=4∙9 OM=2∙3=6h=2∙6=1249 Отже,S=𝐴𝐷+𝐵𝐶2∙CК S=18+82∙12=156 (𝑐м)2  94

22. Знайти: АBCDДано:45 К15 S=5+12∙5=30 (𝑐м)2  

15..... АВСDOДе знаходиться радіус кола описаного навколо прямокутного трикутника??НА СЕРЕДИНІ ГІПОТЕНУЗИ12,5

АВСD15cм25cм. КУ∆АС𝐷(∠С=900):  𝐶𝐷=15см, 𝐴𝐷=25 см, то С𝐷2=АD∙КD 152=25∙KD 225=25∙KDKD=225:25=9( см)МKD=АМ=9( см)ВС=МК=(25-18=7( см)Отже,S=𝐴𝐷+𝐵𝐶2∙CК  АК=16см, К𝐷=9 см, то СК2=АК∙КD  СК2=16∙9 СК=4∙3=12 S=25+72∙12=192 (𝑐м)2  

2. Знайти: K?6005 Дано: АBCMP6005 1 1 3002 2 S,РS=а+𝑏2∙h S=5+72∙h 

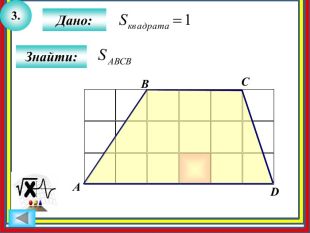
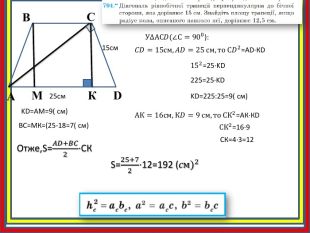
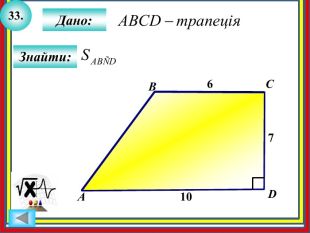
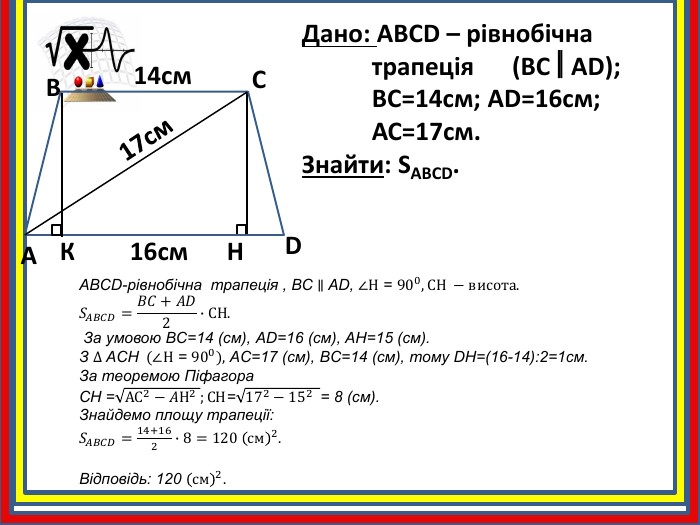
Дано: ABCD – рівнобічна трапеція (BCAD); BC=14см; AD=16см; АС=17см. Знайти: SABCD. ABCD14cм16cм. H17cм. КABCD-рівнобічна трапеція , BC ∥ AD, ∠Н = 900, СН −висота.𝑆𝐴𝐵𝐶𝐷=𝐵𝐶+𝐴𝐷2∙СН. За умовою BC=14 (см), АD=16 (см), AН=15 (см). З ∆ AСН  (∠Н = 900), AС=17 (см), BС=14 (см), тому DH=(16-14):2=1см. За теоремою Піфагора. СН =АС2−𝐴Н2 ;СН=172−152  = 8 (см). Знайдемо площу трапеції: 𝑆𝐴𝐵𝐶𝐷=14+162∙8=120 см2. Відповідь: 120 см2. 

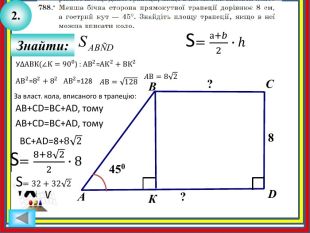
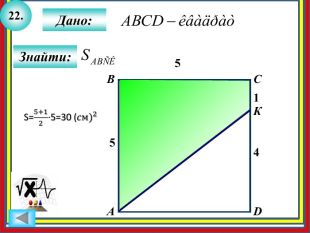
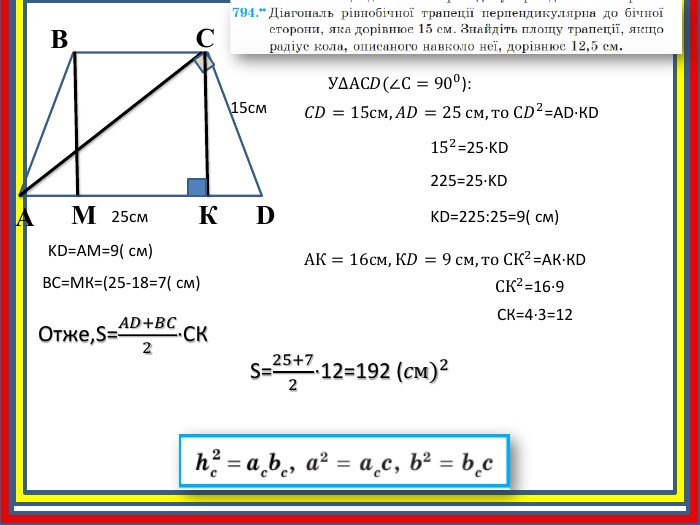
АВСД - прямоуг. трапеція ,  АД║ВС ,  ∠А=∠В=90° , ВС=ВДСН⊥АД ,  СН∩ВД=К ,  СК=20 см ,  КН=12 см . СК: КН=20:12 ⇒ СК: КН=5:3ΔВСД - равнобедрений, т.як. ВС=СД   ⇒   ∠ВСД=∠СДВ .∠ВСД=∠ВДА   як є внутрішні різносторонні АД і ВС и                       січной ВД   ⇒∠СВД=∠ВДА  ⇒  ВД - бісектрисаΔСДН:  ВК - бісектриса, за властивістю: СК: СД=КН: ДН  ⇒  СД: ДН=5:3  ⇒  СД=5х , ДН=3х .  СН²=СД²-ДА²=(5х)²-(3х)²=16х²  ⇒  СН=4х  ,  4х=(20+12)  , 4х=32 , х=8 СД=5·8=40 (см) ,  ДН=3·8=24 (см)  ВС=СД=40 см  ⇒  АН=ВС=40 см ( як протиле сторони прямк. АВСН  ⇒   АД=АН+НД=40+24=64 (см)S(АВСД)=(АД+ВС):2·СН=(64+40):2·32=1664 (см²)Більша діагональ прямокутної трапеції ділить висоту проведену з вершини тупого кута на відрізки завдовжки 20см і 12см. більша бічна сторона трапеції дорівнює її меншій основі. знайдіть площу трапеціїАВБільша діагональ прямокутної трапеції ділить висоту проведену з вершини тупого кута на відрізки завдовжки 20см і 12см. більша бічна сторона трапеції дорівнює її меншій основі. знайдіть площу трапеціїСD

33. Знайти: АBCDДано:7610

Площа трапеції: S =𝒂+𝒃𝟐∙ ha і b – основи трапеції, h – висота трапеції Основи трапеції дорівнюють 7 см і 13 см, а її площа - 40 см2. Знайдіть висоту трапеції. Площа трапеції дорівнює 36 см2, а її основи - 8 см і 10 см. Знайдіть висоту трапеції.

Площа трапеції: S =𝒂+𝒃𝟐∙ ha і b – основи трапеції, h – висота трапеції Висота трапеції дорівнює 6 см, а її площа - 24 см2. Знайдіть суму основ трапеції.. Висота трапеції дорівнює 8 см, а площа - 40 см2. Знайдіть середню лінію трапеції.

Площа трапеції: S =𝒂+𝒃𝟐∙ ha і b – основи трапеції, h – висота трапеції Площа трапеції дорівнює 63 см2, одна з її основ - 5 см, а висота - 7 см. Знайдіть другу основу трапеції. Одна з основ трапеції дорівнює 17 см, а її висота - 3 см. Знайдіть другу основу трапеції, якщо її площа дорівнює 33 см2.

2. Знайти: K?6005 Дано: АBCMP6005 AM=7(cм) 1 1 2

2. Знайти: K4 Дано: АBCDP4 AD=20(cм) 8 8 10 10 У ∆АВК (∠К=900): ВК2=АВ2−АК2 ВК2=102−82 ВК=6см. S=4+202∙6=72 

Площа трапеції: S =𝒂+𝒃𝟐∙ ha і b – основи трапеції, h – висота трапеції Висота трапеції дорівнює 6 см, а її площа - 24 см2. Знайдіть суму основ трапеції.. Висота трапеції дорівнює 8 см, а площа - 40 см2. Знайдіть середню лінію трапеції.

Перевір себе:1)Що називається трапецією?2)Як називаються сторони трапеції?4)Що відомо про кути трапеції, які прилягаютьдо бічної сторони?5)Що називається середньою лінією трапеції?6)Чому дорівнює середня лінія трапеції?7)Що називається висотою трапеції?3)Які види трапецій ви знаєте?