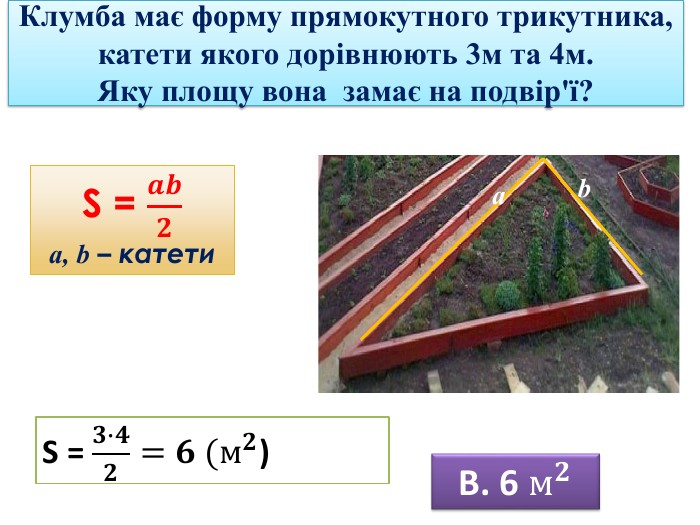
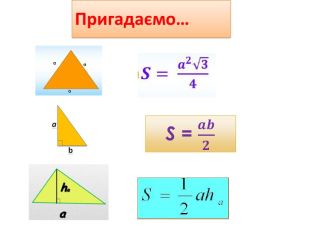
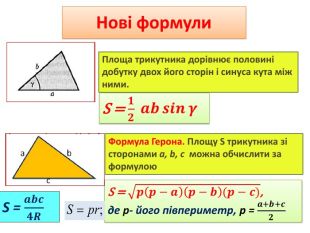
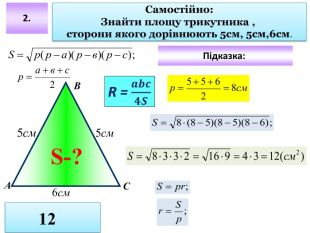
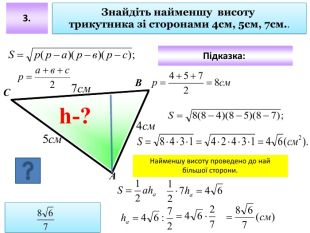
Площа трикутника.Формула Герона. Презентація
Про матеріал
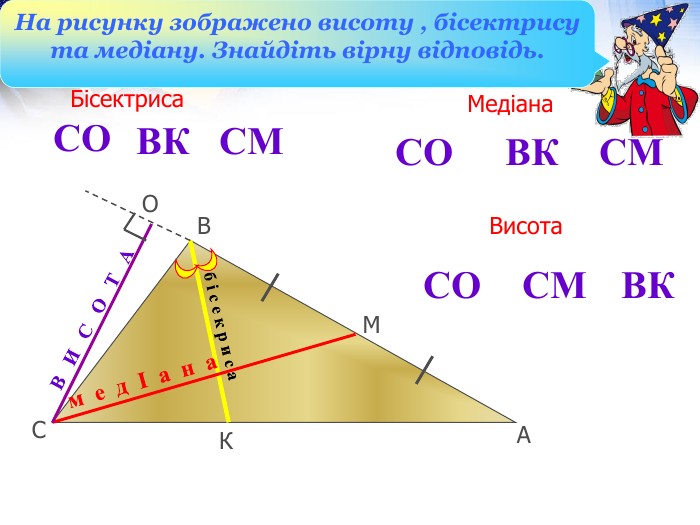
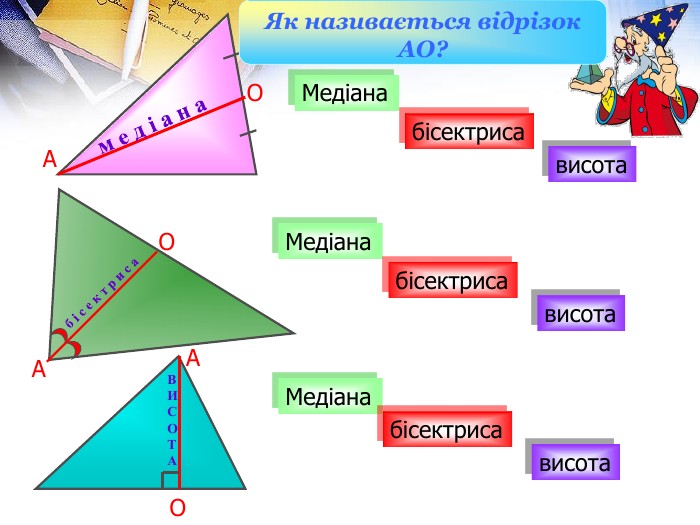
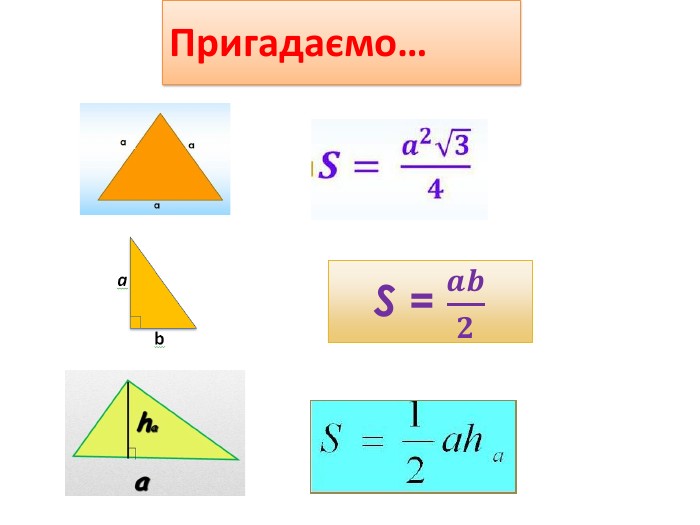
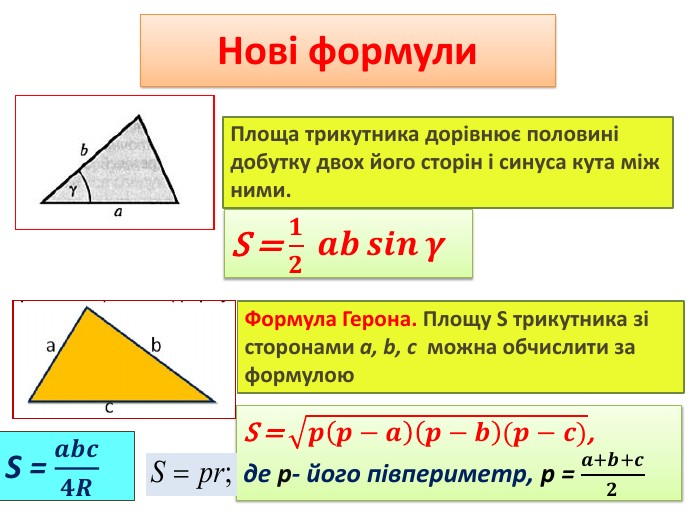
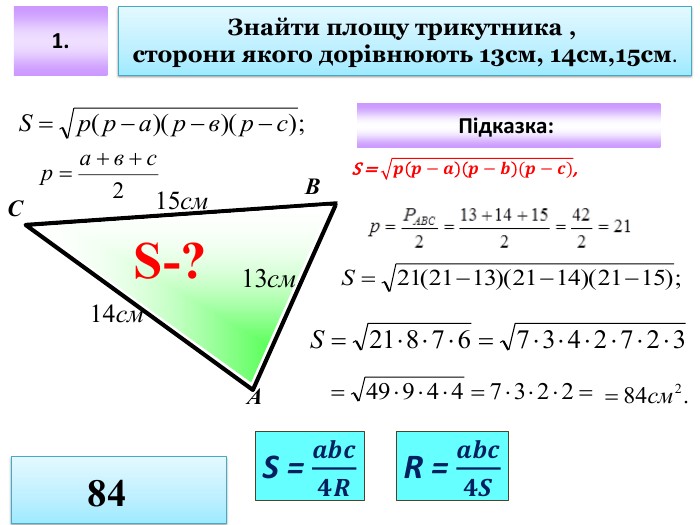
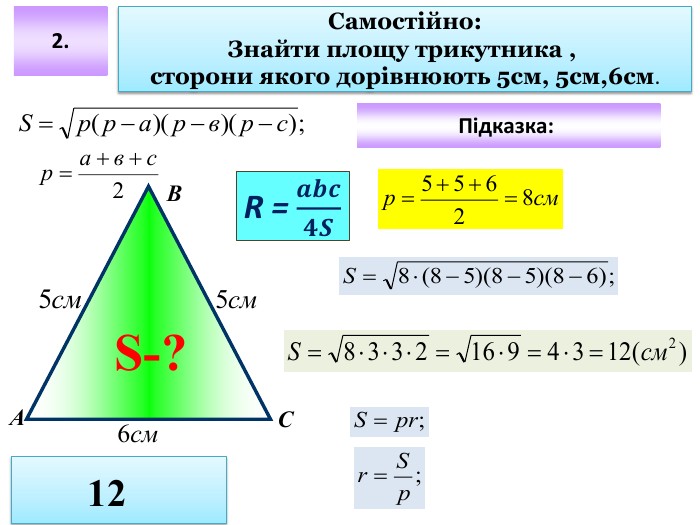
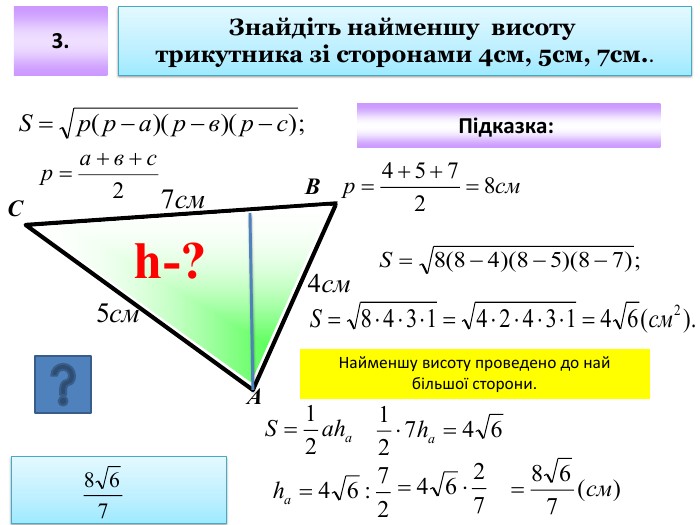
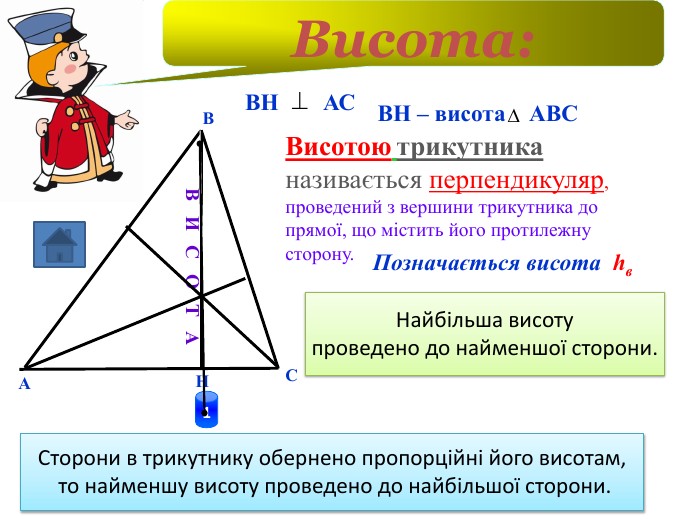
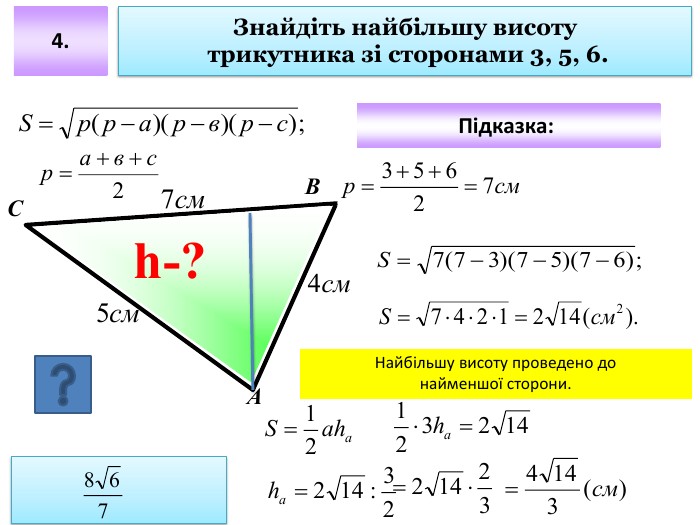
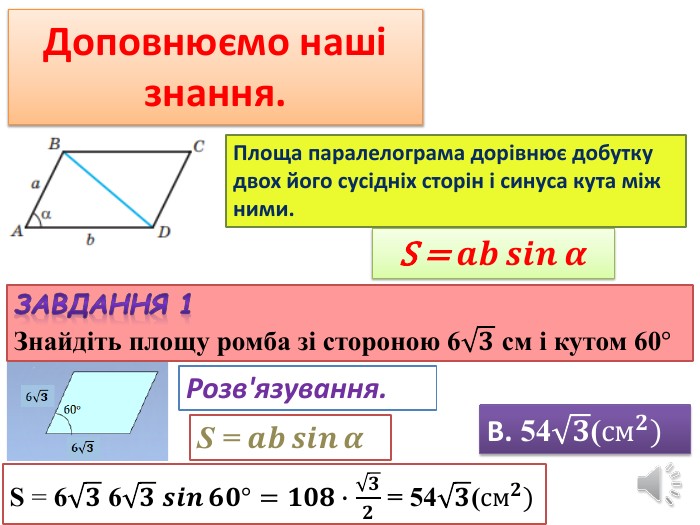
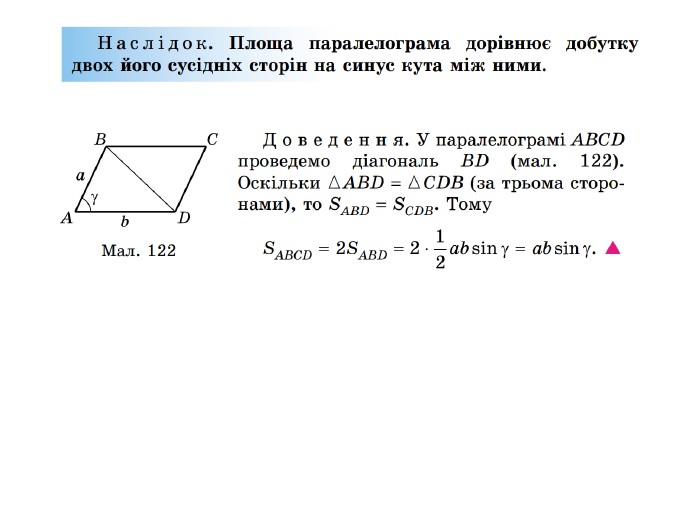
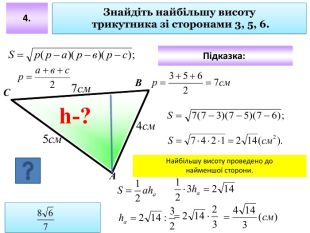
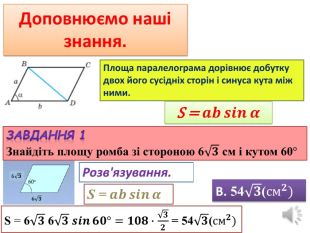
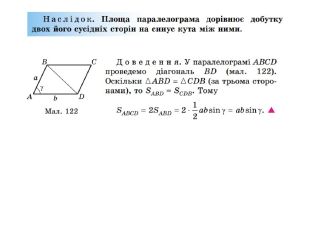
Презентація до уроку "Площа трикутника" .Можна використовувати для проведення уроків при дистанційному навчанні. Містить основні етапи уроку: фронтальне опитування, усні вправи, задачі з повними поясненням, підсумок уроку, рефлексію. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку