Посібник для уроків математики І семестр 6 класу (оновлений)
Ківерцівська експериментальна школа
Навчальний посібник

І семестр


Любий шестикласнику!
 Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. В оволодінні навчальним матеріалом курсу тобі допоможе цей посібник. Він складається з п’яти блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. В оволодінні навчальним матеріалом курсу тобі допоможе цей посібник. Він складається з п’яти блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Будь уважний, активний і наполегливий, не лінуйся і таким чином принесеш радість собі, своїм батькам і Творцю.
Нехай Бог посилає мудрості у вивченні математики!!!
Тема №1. Подільність чисел
Урок №1

Подільність чисел
Арифметика – це лічильна мудрість. Без цієї
мудрості ні філософа, ні лікаря не може бути.
Леонтій Магницький
Питання
- Дільники і кратні.
- Ознаки подільності на 2, 5, 10, 3, 9.
- Прості та складені числа.
- Найбільший спільний дільник.
- Найменше спільне кратне.
Література
Істер О.С. Математика: підручник для 6 класу загальноосвітніх навчальних закладів. – К.: Генеза, 2014, §§1 – 7, ст. 5 – 29.
|
1. Дільники і кратні |
||
|
1.1 |
Дільником натурального числа а називають натуральне число, на яке а ділиться без остачі. |
2, 3, 4 – дільники числа 12 |
|
1.2 |
Кратним натуральному числу а називають натуральне число, яке ділиться на а. |
24, 36, 48,… - кратні числу 12 |
|
2. Ознаки подільності на 10, 5, 2, 9, 3 |
||
|
2.3 |
На 10 діляться всі ті натуральні числа, запис яких закінчується цифрою 0. |
20; 2000; 520 |
|
2.4 |
На 5 діляться всі ті натуральні числа, запис яких закінчується цифрою 0 або цифрою 5. |
10, 55, 40, 75 |
|
2.5 |
На 2 діляться всі ті натуральні числа, запис яких закінчується парною цифрою. |
120; 32; 48 |
|
2.6 |
На 9 діляться всі ті натуральні числа, сума цифр яких ділиться на 9. |
2571: 2 + 5 + 7 + 1 |
|
2.7 |
На 3 діляться всі ті натуральні числа, сума цифр яких ділиться на 3. |
|
|
3. Прості і складені числа |
||
|
3.8 |
Натуральне число називають простим, якщо воно має тільки два різних дільники: одиницю і саме це число. |
7; 13; 113 |
|
3.9 |
Натуральне число називають складеним, якщо воно має більше двох дільників. |
24 – 1, 2, 3, 4, 6, 8, 12, 24 |
|
3.10 |
Будь – яке складене число можна подати у вигляді добутку простих чисел, тобто розкласти на прості множники. |
10 = 2 ∙ 5 18 = 2 ∙ 3 ∙ 3 = 2 ∙ 3² |
|
3.11 |
Розкладом простого числа на прості множники вважатимемо саме це число. |
|
|
4. Найбільший спільний дільник |
||
|
4.12 |
Найбільшим спільним дільником кількох натуральних чисел (НСД) називають найбільше натуральне число, на яке ділиться кожне з даних чисел. |
НСД (6; 8) = 2 НСД (12; 18) = 6 |
|
4.13 |
Найбільший спільний дільник кількох чисел дорівнює добутку спільних простих множників цих чисел.
|
12 = 2 ∙ 2 ∙ 3 18 = 2 ∙ 3 ∙ 3 НСД (12;18)= 2 ∙ 3 =6 |
|
4.14 |
Щоб знайти НСД кількох чисел достатньо: 1) розкласти дані числа на прості множники; 2) виписати всі спільні прості множники в знайдених розкладах і обчислити їх добуток. |
|
|
4.15 |
Два натуральних числа, НСД яких дорівнює 1, називають взаємно простими числами. |
15 і 7; 13 і 17 |
|
5. Найменше спільне кратне |
||
|
5.16 |
Найменшим спільним кратним кількох натуральних чисел (НСК) називають найменше натуральне число, яке ділиться на кожне з даних чисел. |
НСК (10,15) = 30 НСК (12; 24) = 24 |
|
5.17 |
Щоб знайти НСК двох чисел достатньо: 1) розкласти дані числа на прості множники; 2) доповнити розклад одного з них тими множниками розкладу другого числа, яких не вистачає в розкладі першого; 3) обчислити добуток знайдених множників. |
12 = 2 ∙ 2 ∙ 3 18 = 2 ∙ 3 ∙ 3 НСК (12; 18) = 2 ∙ 2 ∙ 3 ∙ 3 = 4 ∙ 9 = 36
|
Урок №2
«У Господньому страхові сильна надія,
і Він пристановище дітям Своїм»
Приповісті Соломонові 14:26
Фронтальне опрацювання матеріалу
Дільники і кратні натурального числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
Повторіть тези 1.1. – 1.2. блоку №1 і дайте відповіді на питання:
1) Що називають дільником числа а?
2) Що називають кратним числу а?
Завдання 2.
2.1. Усно розв’язати вправи
- Чому дорівнює частка при діленні 54 на 9?
- Чому дорівнює дільник, якщо ділене дорівнює 98, а частка – 7?
- Чому дорівнює ділене, якщо дільник дорівнює 24, а частка – 5?
2.2. Перегляньте презентацію, запропоновану вчителем.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконати вправи
- Напишіть усі дільники чисел 18, 8, 13, 56.
- Напишіть чотири числа, які кратні числам 7, 30, 100, 34.
- Серед чисел 83, 95, 72, 64, 100, 75 знайдіть кратні числу 5 і запишіть їх у порядку зростання.
- Із чисел 7, 8, 9, 10, 11 випиши спочатку всі прості числа, а потім – усі складені.
- Виконати вправу 13 ст. 7.
- Виконати вправу 16 ст. 8.
- Виконати вправу 21 ст. 8.
- Виконати вправу 24 ст. 8.
- Усно виконати завдання на кубику «Дільники і кратні».
Урок №3
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Ознаки подільності на 2, 5, 10
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.5 блоку № 1.
- Усно дай відповідь на питання:
- Що називають дільником натурального числа а?
- Яке число називають кратним натуральному числу а?
- Сформулюй ознаку подільності на 10.
- Сформулюй ознаку подільності на 5.
- Сформулюй ознаку подільності на 2.
Завдання 2.
Усно виконай вправи, запропоновані вчителем.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправи, стор. 10 підручника: 33, 36, 37.
Завдання 4.
Письмово виконай вправи, стор. 10 – 11 підручника: 38, 40.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
- Письмово виконай вправу, стор. 10 підручника: 42.
- Виконай завдання на кубику «Подільність чисел на 2, 5, 10».
Урок №4
«Горіх без зерна ніщо, а людина без серця»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Ознаки подільності на 3 та 9
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.7 блоку № 1.
- Усно дай відповідь на питання:
- Що називають дільником натурального числа а?
- Яке число називають кратним натуральному числу а?
- Сформулюй ознаку подільності на 10.
- Сформулюй ознаку подільності на 5.
- Сформулюй ознаку подільності на 2.
- Сформулюй ознаку подільності на 9.
- Сформулюй ознаку подільності на 3.
Завдання 2.
Усно виконай вправи, запропоновані вчителем.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправи, стор. 13 підручника: 48; 50.
Завдання 4.
Письмово виконай вправи, стор. 13 підручника: 52; 54; 56.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
 Завдання 5.
Завдання 5.
5.1. Письмово виконай вправи, стор. 14 підручника: 59.
5.2. ЗАФАРБУЙ НОМЕРИ ЖОВТИМ КОЛЬОРОМ
Урок №5
«Людина дивиться на лице, а Бог на серце»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Прості і складені числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.9 блоку № 1.
- Усно дай відповідь на питання:
- Що називають дільником натурального числа а? Наведи декілька прикладів.
- Яке число називають кратним натуральному числу а? Наведи декілька прикладів.
- Сформулюй ознаку подільності на 10.
- Сформулюй ознаку подільності на 5.
- Сформулюй ознаку подільності на 2.
- Сформулюй ознаку подільності на 9.
- Сформулюй ознаку подільності на 3.
- Яке натуральне число називають простим? Назви декілька простих чисел.
- Яке натуральне число називають складеним? Назви декілька складених чисел.
Завдання 2.
- Уважно прослухай історичну довідку щодо вивчення простих і складених чисел, запропоновану учителем.
- Користуючись таблицею простих чисел, усно виконай вправи:
- Назви перші десять простих чисел.
- Назви найменше просте число? Парним чи непарним є це число? Знайди ще парні прості числа. Зроби висновок.
- Чи є числа 87; 47 простими?
- Назви всі прості числа, які більші за 40, але менші за 50.
- Яке просте число слідує за числом 14?
- Знайди пари простих чисел, різниця між якими дорівнює 2 (числа – близнюки).
- Знайдіть трійки простих чисел такі, щоб різниця між кожним наступним і попереднім дорівнювала 2 (прості трійні).
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправи, стор. 16 підручника: 67; 69.
Завдання 4.
Письмово виконай вправи, стор. 16 підручника: 71; 72.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
- Письмово виконай вправи, стор. 17 підручника: 76; 77.
- Щоб гарно підготуватись до ІОМ і пригадати все, що ти знаєш, пройди тест, запропонований вчителем у блозі.

Готуємось до індивідуального опрацювання
- Серед чисел 46, 35, 17, 19, 23 вкажи ті, які мають лише два дільники.
- Серед чисел 5, 34, 26, 123, 57, 98 вкажи парні та непарні.
- Які цифри можна підставити замість зірочки, щоб число 4*3* ділилось без остачі на 3 і на 10 одночасно?
-
Запиши всі числа, які задовольняють нерівності
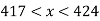 та кратні числу 2.
та кратні числу 2.
Урок №7
«Тоді лише пізнається цінність часу,
коли він утрачений»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Розкладання чисел на прості множники
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.11 блоку № 1.
- Усно дай відповідь на питання:
- Що називають дільником натурального числа а?
- Яке число називають кратним натуральному числу а?
- Сформулюй ознаку подільності на 10.
- Сформулюй ознаку подільності на 5.
- Сформулюй ознаку подільності на 2.
- Сформулюй ознаку подільності на 9.
- Сформулюй ознаку подільності на 3.
- Яке натуральне число називають простим?
- Яке натуральне число називають складеним?
- Як можна подати будь-яке складене число?
- Що є розкладом простого числа на прості множники?
Завдання 2.
- Уважно прочитай матеріал § 5, стор. 18 – 19.
- Користуючись прочитаним текстом, дай відповідь на питання:
- Що доцільно використовувати при розкладанні числа на прості множники? (стор. 18)
- Чим можна замінити добуток однакових множників у розкладі числа на прості множники? (стор. 19)
-
Як знайти всі дільники числа, використовуючи розклад числа на прості множники? (стор. 19)
- Усно виконай вправу 83, стор. 19.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправу 85, стор. 19.
Завдання 4.
Письмово виконай вправи, стор. 19 – 20 підручника: 87; 89.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Письмово виконай вправи, стор. 20 підручника: 90; 91.
Урок №8
«Хіба не любов усе єднає, будує, творить,
подібно до того, як ворожість руйнує »
Григорій Сковорода
Фронтальне опрацювання матеріалу
Найбільший спільний дільник
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 4.15 блоку № 1.
- Усно дай відповідь на питання:
- Що називають дільником натурального числа а?
- Яке число називають кратним натуральному числу а?
- Сформулюй ознаку подільності на 10.
- Сформулюй ознаку подільності на 5.
- Сформулюй ознаку подільності на 2.
- Сформулюй ознаку подільності на 9.
- Сформулюй ознаку подільності на 3.
- Яке натуральне число називають простим?
- Яке натуральне число називають складеним?
- Як можна подати будь-яке складене число?
- Що є розкладом простого числа на прості множники?
- Що називають найбільшим спільним дільником кількох натуральних чисел?
- Чому дорівнює найбільший спільний дільник?
- Як знайти найбільший спільний дільник кількох чисел?
- Які числа називаються взаємно простими?
Завдання 2.
Усно виконай вправи, стор. 23 підручника: 96; 97; 98.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправи, стор. 23 підручника: 102 (1, 3, 5); 105.
Завдання 4.
Письмово виконай вправу, стор. 24 підручника: 109.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
5.1. Письмово виконай вправу, стор. 24 підручника: 113.
5.2.

Урок №9
Фронтальне опрацювання матеріалу
Найбільший спільний дільник
Виконати роботу у практичному зошиті «Я дослідник», тема 1.
Уроки №10, 11
«Любов нехай буде нелицемірна;
ненавидьте зло та туліться до доброго!»
Послання апостола Павла до римлян 12:9
Фронтальне опрацювання матеріалу
Найменше спільне кратне
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок №1.
- Дай відповіді на питання:
- Яке число називається складеним?
- Які числа називаються простими?
- Дайте визначення кратному.
- Що називають найменшим спільним кратним?
- Який алгоритм знаходження найменшого спільного кратного?
- Дайте визначення найбільшому спільному дільнику.
-
Яке число називається дільником числа
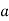 ?
?
- Які числа називаються взаємно простими?
Завдання 2.
2.1. Назви три натуральних числа, кратних 2; 5.
2.2. Назви будь-яке число, яке ділиться:
1) на 3 і на 4; 2) на 6 і на 18.
Завдання 3.
Розглянь приклад розв’язування вправи:
Знайти НСК(24; 60)
- Розкласти числа на прості множники
![]()
![]() 24 2 60 2
24 2 60 2
12 2 30 2
6 2 15 3
3 3 5 5
1 1
![]()
2. До розкладу першого числа дописати з розкладу другого ті множники, яких немає в розкладі першого.
3. Знайти добуток цих множників
![]()
4. Зробити висновок
НСК(24; 60)=120.
ІІ. Відпрацювання умінь та навичок розв’язування задач і вправ
Завдання 4.
- Знайдіть НСК чисел:
- 12 і 18;
- 8 і 16;
- 9 і 14;
- 36 і 48;
- 210 і 350;
-
12; 15; 18.
- Знайдіть найменше спільне кратне знаменників дробів:
-

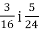 ;
;
-
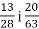 .
.
- Довжина кроку батька дорівнює 75 см, довжина кроку сина – 50 см. Яку найменшу однакову відстань має пройти кожний з них, щоб вони обидва зробили по цілому числу кроків?
- Знайдіть НСК:
- Перших п’яти парних чисел;
- Перших чотирьох складених чисел.
- Одиничці і Нулику було запропоновано знайти НСК чисел 56 і 70. Ось як вони це зробили:
![]()
![]()
![]()
![]() Одиничка: Нулик:
Одиничка: Нулик:
56 2 70 2 56 4 70 5
28 2 35 5 14 7 14 7
14 2 7 7 2 2 2 2
7 7 1 1 1
1
![]()
Хто виконав розкладання на множники невірно?
- Дмитро і Павло одночасно вирушили в похід з одного пункту в одному напрямі, проте Павло робив зупинку для відпочинку через кожні 2400 м, а Дмитро – через кожні 2800 м. На якій найменшій відстані від початку походу місця їх зупинок співпадуть?
- Виконати вправу 125 (4, 5, 6) ст. 27.

Готуємось до індивідуального опрацювання
- Знайди НСД чисел 55 і 132.
- Знайди НСК чисел 56 і 35..
- Знайди найбільший спільний дільник чисел 660 і 495.
- Учень розставив книжки порівну на восьми полицях, о потім переставив їх теж порівну на дванадцяти полицях. Скільки книжок в учня, якщо їх більше за 93, але менше ніж 117?
-
 Знайди НСК чисел 12, 15 і 18.
Знайди НСК чисел 12, 15 і 18.
- Знайди НСД чисел 28, 84 і 98.
- Між учнями 6 класу поділили порівну 84 мандарини та 56 апельсинів. Скільки учнів у класі, якщо відомо, що їх більше ніж 25?
Урок №13
"Мудрість мужчини – промовчати…»
Ліна Костенко
Внутрішньопредметне узагальнення матеріалу
Подільність чисел
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 1.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
- Знайди всі дільники числа 36
|
А |
Б |
В |
Г |
|
3, 6 |
1, 2, 3, 6 |
1, 2, 3, 4, 6, 9, 12, 18, 36 |
3, 6, 12 |
- Із чисел 2, 3, 8, 6, 7, 15 і 30 вибери прості числа.
|
А |
Б |
В |
Г |
|
2, 3, 6 |
2, 3, 8 |
2, 3, 7 |
2 |
- Знайди три числа, кратні 20.
|
А |
Б |
В |
Г |
|
5, 4, 10 |
3, 5, 6 |
10, 15, 30 |
40, 60, 100 |
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
- Із чисел 1, 2, 3, 4, 6, 8, 15, 28 і 45 випиши спочатку всі прості, а потім – усі складені числа.
- Знайди найбільший спільний дільник чисел 12 і 28.
- Розклади на прості множники числа 1260; 820.
- Знайди найменше спільне кратне чисел 210 і 350.
- Довжина кроку батька дорівнює 60 см, довжина кроку сина 45 см. Яку найменшу однакову відстань має пройти кожен з них, щоб вони обидва зробили по цілому числу кроків?
Тема №2. Звичайні дроби. Додавання і віднімання звичайних дробів
Урок №1

Звичайні дроби. Додавання і віднімання звичайних дробів
«Математика – цариця наук і
арифметика – цариця математики»
Карл Гаусс
Питання
- Поняття дробу. Основна властивість дробу. Скорочення дробу.
- Зведення дробів до спільного знаменника. Порівняння дробів.
- Додавання і віднімання дробів та мішаних чисел.
- Перетворення звичайних дробів у десяткові. Десяткове наближення звичайного дробу.
Література
Істер О.С. Математика: підручник для 6 класу загальноосвітніх навчальних закладів. – К.: Генеза, 2014, §§ 8 – 13, ст. 30 – 61.
|
1. Поняття дробу. Основна властивість дробу |
||
|
1.1 |
Коли один предмет або одиницю виміру ділять на рівні частини, виникають дробові числа. |
Півхлібини, чверть, третина |
|
1.2 |
Основна властивість дробу Якщо чисельник і знаменник дробу помножити або поділити на одне й те саме відмінне від нуля число, то отримаємо дріб, що дорівнює даному. |
|
|
1.3 |
Ділення чисельника і знаменника дробу на одне й те саме число називається скороченням дробу. |
|
|
1.4 |
Дріб, чисельник і знаменник якого – взаємно прості числа, називається нескоротним дробом. |
|
|
2. Зведення дробів до спільного знаменника. Порівняння дробів |
||
|
2.5 |
Найменше спільне кратне знаменників кількох дробів називають найменшим спільним знаменником. |
|
|
2.6 |
Щоб звести дроби до найменшого спільного знаменника треба:
|
|
|
2.7 |
З двох дробів з однаковими знаменниками більший той, у якого більший чисельник. |
|
|
2.8 |
З двох дробів з однаковими чисельниками більший той, у якого менший знаменник. |
|
|
2.9
|
Щоб порівняти два дроби з різними знаменниками, достатньо звести їх до спільного знаменника, і порівняти одержані дроби. |
|
|
3. Додавання і віднімання дробів та мішаних чисел |
||
|
3.10 |
Щоб додати (відняти) дроби з однаковими знаменниками, потрібно додати (відняти) їх чисельники, а знаменник залишити тим самим. |
|
|
3.11 |
Щоб додати (відняти) дроби з різними знаменниками, достатньо:
|
|
|
3.12 |
Для додавання мішаних чисел використовуються переставна і сполучна властивості додавання:
|
|
|
3.13 |
При відніманні мішаних чисел використовуються властивості віднімання числа від суми і суми від числа:
|
|
|
4. Перетворення звичайних дробів у десяткові. Десяткове наближення звичайного дробу. |
||
|
4.14 |
Щоб перетворити звичайний дріб у десятковий, достатньо чисельник поділити на знаменник. |
|
|
4.15 |
Щоб знайти десяткове наближення звичайного дробу, яке округлюється до даного розряду достатньо:
|
4,5(3) = 4,53333… |
Уроки №2 – 4
«І все, що тільки чините,
робіть від душі, як Господу, а не людям»
Послання св. апостола Павла до Колосян 3 : 23
Фронтальне опрацювання матеріалу
Основна властивість дробу. Скорочення дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.4 блоку №2.
- Усно дай відповіді на питання:
- Коли виникають дробові числа?
- Сформулюй основну властивість дробу.
- Що називають скороченням дробів?
- Який дріб називається нескоротним?
-
Прочитай дроби, назви чисельник і знаменник дробів:
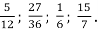
- Що показує знаменник дробу, що показує чисельник?
-
Виділіть цілу частину з дробу
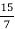 .
.
-
Порівняйте дроби
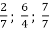 з одиницею.
з одиницею.
-
Замініть дріб
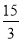 натуральним числом.
натуральним числом.
Завдання 2.
2.1. Запам’ятай основні способи скорочення дробів (презентація).
2.2. Виконай усно вправи, стор. 32 – 33 підручника: 137, 138.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Виконай письмово вправи, стор.33 – 34 підручника: 148, 152 (1, 3), 153 (1, 3, 5, 7, 9), 156, 157, 163, 165.
Завдання 4.
Виконай письмово вправу:
Запиши дріб ![]() .
.
1) Помнож його чисельник і знаменник на 7 і запиши відповідну рівність.
2)Поділи його чисельник і знаменник на 2 і запиши відповідну
рівність.
3) Запиши три дроби, що дорівнюють даному з меншим знаменником.
4) Запиши три дроби, що дорівнюють даному з більшим знаменником.
5) Запишіть його дробом зі знаменником 96.
6) Поділи його чисельник і знаменник на НСД чисельника і знаменника.
Завдання 5.
Виконати вправи на експрес-картках, запропонованих вчителем.
Уроки №5, 6
«Ми прийшли в цей світ, щоб допомагати
один одному в нашій подорожі по життю»
Уїльям Джеймс, американський психолог і філософ
Фронтальне опрацювання матеріалу
Найменший спільний знаменник дробів. Зведення дробів до спільного знаменника
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.6 блоку № 2.
- Продовж речення:
- Нескоротним дробом називають дріб, у якого чисельник і знаменник …
- Найменший спільний знаменник дробів – це …
- Ділення чисельника і знаменника дробу на одне і те ж саме число називається …
- Щоб звести дроби до найменшого спільного знаменника потрібно …
- Дробові числа виникають коли…
Завдання 2.
Виконай усно вправи, стор. 39 підручника: 176; 179.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово виконай вправу 181 (2, 4, 6, 8), стор. 38 підручника.
Завдання 4.
- Розглянь приклади 2, 3, стор. 38 підручника.
- Користуючись розглянутими прикладами, виконай письмово вправу 187, стор. 40.
Завдання 5.
Виконай письмово вправу 192, стор. 40.
Завдання 6.
Письмово виконай вправи, стор. 41 підручника: 202; 205.
Уроки №7, 8
«Моя любов – це Україна і математика»
М.П. Кравчук, український математик
Фронтальне опрацювання матеріалу
Порівняння дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.9 блоку № 2.
- Встав пропущені слова і словосполучення:
-

 Значення дробу не зміниться, якщо чисельник і знаменник дробу або
Значення дробу не зміниться, якщо чисельник і знаменник дробу або  на одне і те саме
на одне і те саме  від
від  число.
число.
- Найменший спільний знаменник дробу – це їх знаменників.
-
 Щоб порівняти два дроби з різними знаменниками, достатньо звести їх до і
Щоб порівняти два дроби з різними знаменниками, достатньо звести їх до і  одержані дроби.
одержані дроби.
-
 Ділення чисельника і знаменника дробу на одне й те ж саме число називається
Ділення чисельника і знаменника дробу на одне й те ж саме число називається  .
.
- Дріб, чисельник і знаменник якого – числа, називається нескоротним.
- Щоб звести дроби до спільного знаменника треба:
-
знайти
 цих дробів;
цих дробів;
-
 знайти
знайти  до кожного дробу, поділивши
до кожного дробу, поділивши  на знаменника даних дробів;
на знаменника даних дробів;
- помножити чисельник кожного дробу на його .
-
З двох дробів з однаковими знаменниками більший той, у якого
 .
.
-
З двох дробів з однаковими чисельниками більший той, у якого
 .
.
Завдання 2.
Виконай усно вправу 180, стор. 39 підручника.
Завдання 3.
Усно виконай вправи:
-
Які з дробів
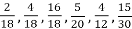 дорівнюють
дорівнюють  ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Скороти дроби:
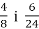 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Зведи дроби
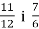 до найменшого спільного знаменника.
до найменшого спільного знаменника.
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
Виконай письмово вправи, стор. 39 – 40 підручника: 183; 185; 189.
Завдання 5.
Виконай письмово вправи, стор. 40 – 41 підручника: 194; 195; 197; 198.
Завдання 6.
Виконай письмово вправи:
- Один секретар друкує 48 сторінок тексту за 9 год, а інший – 68 сторінок за 12 год. Хто з них працює швидше?
- Триметрову колоду розпиляли на 7 однакових частин, а чотириметрову – на 10. Частина якої колоди довша?
-
Михайло, Юра і Ніна розв’язували в класі одну і ту ж задачу. Один із них витратив на розв’язування
 уроку, інший
уроку, інший  уроку, а третій
уроку, а третій 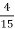 уроку. Яку частину уроку витратив на розв’язування кожен із них, коли відомо, що Ніна розв’язала задачу швидше, ніж Михайло, а Юра швидше, ніж Ніна?
уроку. Яку частину уроку витратив на розв’язування кожен із них, коли відомо, що Ніна розв’язала задачу швидше, ніж Михайло, а Юра швидше, ніж Ніна?
- В класі 7 дівчаток і 10 хлопчиків. Із них 2 дівчинки і 3 хлопчики носять окуляри. Хто краще бачить – дівчатка чи хлопчики?
- В 4-літрову каструлю з водою господиня кинула три столові ложки солі, а в 3-літрову – дві. В якій каструлі розчин виявився солонішим?
Завдання 7.
Письмово виконай вправи:
-
Зведи дроби
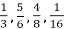 до знаменника 48.
до знаменника 48.
- Яку частину доби становлять 3 год, 5 год, 8 год?
- Порівняй дроби:
![]() ;
;
![]() ;
;
- Вантажна машина проїжджає 9 км за 14 хв, а автобус 5 км за 9 хв. У кого з них швидкість більша?

Готуємось до індивідуального опрацювання
-
Зведи дроби
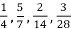 до знаменника 56.
до знаменника 56.
- Яку частину години становлять 3 хв, 20 хв, 48 хв?
- Порівняй дроби:
-
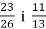 ;
;
-
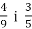 .
.
-
Розташуй в порядку спадання числа:
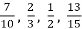 .
.
-
 Першу головку сиру масою 9 кг розрізали на 16 рівних частин, а другу головку масою 7 кг – на 10 рівних частин. Частина якої головки – першої чи другої – має більшу масу?
Першу головку сиру масою 9 кг розрізали на 16 рівних частин, а другу головку масою 7 кг – на 10 рівних частин. Частина якої головки – першої чи другої – має більшу масу?
Уроки №10, 11
«Той, хто не любить своєї
країни, нічого любити не може»
Джордж Байрон, англійський поет
Фронтальне опрацювання матеріалу
Додавання і віднімання дробів з різними знаменниками
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.11 блоку №2.
- Дай відповіді на питання:
- Сформулюй основну властивість дробу.
- Як порівняти дроби з різними знаменниками?
- Найменший спільний знаменник дробів – це…
- Як додати або відняти дроби з різними знаменниками?
- Як додати або відняти дроби з однаковими знаменниками?
Завдання 2.
-
Каліграфічна хвилинка. Запишіть дріб, чисельник якого – це кількість букв у слові «український», а знаменник дробу – кількість звуків у слові «віночок». (Дріб
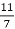 )
)
- Як називається цей дріб?
- Виділити цілу частину з неправильного дробу.
- Усно виконай вправу 206 (1, 3, 5, 7), стор. 43 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 43 підручника: 207 (2, 4, 6, 8); 209.
Завдання 4.
Письмово виконай вправи, стор. 44 – 45 підручника: 211 (1, 3, 5, 7); 218; 223.
Завдання 5.
- Письмово виконай вправи, стор. 45 – 46 підручника: 225; 227; 228; 229.
- Виконати самостійно вправу, запропоновану вчителем у презентації.
Уроки №12, 13
«Дружба подвоює радості і
скорочує наполовину прикрості»
Френсіс Бекон, англійський державний діяч
Фронтальне опрацювання матеріалу
Додавання і віднімання мішаних чисел
І. Робота над засвоєнням понять термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.13 блоку № 2.
- Усно дай відповіді на питання:
- Коли виникають дробові числа?
- Як порівняти дроби з різними знаменниками?
- Як звести дроби до найменшого спільного знаменника?
- Як додати або відняти дроби з різними знаменниками?
- Як додати або відняти дроби з однаковими знаменниками?
- Що використовують при додаванні мішаних чисел?
- Що використовують при відніманні мішаних чисел?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконай вправи, стор. 49 підручника: 237 (1, 3), 239 (2, 4, 6, 8), 241, 244 (1, 3).
Завдання 3.
Самостійно виконай вправу 246, стор. 50 підручника.
Завдання 4.
Письмово виконай вправи, стор. 50 – 52 підручника: 250, 251, 256, 265, 268.
Завдання 5.
Письмово виконай вправи:
-
Лисичка замислила обгородити город, що має форму прямокутника шириною
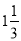 м і довжиною
м і довжиною 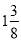 м. Яка довжина огорожі? Допоможіть лисичці.
м. Яка довжина огорожі? Допоможіть лисичці.
-
Мишка-шкрябушка заховала в одну нірку
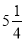 горішків, а скільки в другу – забула, але вона знає, що всього в неї було
горішків, а скільки в другу – забула, але вона знає, що всього в неї було 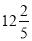 горішків. Допоможіть їй, не витягуючи горішки з першої нірки, дізнатися, скільки горішків у другій нірці?
горішків. Допоможіть їй, не витягуючи горішки з першої нірки, дізнатися, скільки горішків у другій нірці?
-
Старенька Сова замислила полетіти до своєї доньки Совички, яка живе на відстані 4км.
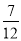 км вона пролетіла без відпочинку. Скільки кілометрів їй потрібно ще пролетіти? Допоможіть старенькій.
км вона пролетіла без відпочинку. Скільки кілометрів їй потрібно ще пролетіти? Допоможіть старенькій.
-
Коти на велосипедах виїхали одночасно з різних кінців назустріч один одному. Швидкість першого кота дорівнює
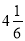 км/год, а другого
км/год, а другого 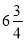 км/год. Через скільки годин після початку руху вони зустрінуться, якщо відстань між ними
км/год. Через скільки годин після початку руху вони зустрінуться, якщо відстань між ними 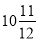 км?
км?
Урок №14
«Щоб дійти до мети,
треба перш за все йти»
Оноре де Бальзак
Фронтальне опрацювання матеріалу
Перетворення звичайних дробів у десяткові. Нескінченні періодичні десяткові дроби
І. Робота над засвоєння понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 4.14 блоку №2.
- Усно дай відповіді на питання:
- Коли виникають дробові числа?
- Як перетворити звичайний дріб у десятковий?
- Як додати або відняти дроби з різними знаменниками?
- Що таке найменший спільний знаменник дробів?
- Як знайти найменший спільний знаменник дробів?
- Як порівняти два дроби з різними знаменниками?
Завдання 2.
- Прочитай § 12, стор.53 – 56 підручника.
- Усно дай відповіді на питання:
- Чи завжди перетворення звичайного дробу у десятковий дає скінченний десятковий дріб?
- Який запис числа називають нескінченним періодичним десятковим дробом?
- Що називають періодом нескінченного періодичного десяткового дробу?
- У якому випадку звичайний нескоротний дріб можна перетворити у скінченний десятковий дріб?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай усно вправу 274, стор. 56 підручника.
Завдання 4.
Виконай письмово вправи, стор. 56 – 57 підручника: 277, 279, 281, 283.
Завдання 5.
Обчисли усно:
|
6 : 10 |
0,2 · 4 |
5 + 0,8 |
0,76 – 0,3 |
|
0,8 : 2 |
2,1 ·3 |
0,23 + 7 |
2,54 – 2 |
|
2,1 : 7 |
0,7 · 10 |
0,48 + 0,2 |
0,82 – 0,02 |
|
0,5 : 10 |
0,5 · 2 |
0,6 + 0, 34 |
0,63 – 0,6 |
|
4,1 : 2 |
0,25 · 4 |
2,7 + 1,12 |
0,8 – 0,25 |
Урок №15
«Коли дому Господь не будує, даремно працюють його
будівничі при ньому! Коли міста Господь не пильнує, даремно сторожа чуває!»
Псалом 126:1
Фронтальне опрацювання матеріалу
Десяткове наближення звичайного дробу
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Прочитай § 13, стор. 58 підручника.
- Повтори блок №2.
- Усно дай відповіді на питання:
- За якої умови виникають дробові числа?
- Як знайти десяткове наближення звичайного дробу?
- Як перетворити звичайний дріб у десятковий?
- Як порівняти дроби з різними знаменниками?
- Як додати або відняти дроби з однаковими знаменниками? З різними знаменниками?
- Що показує знаменник і чисельник дробу?
- Що означає скоротити дріб?
- Сформулюй основну властивість дробу.
Завдання 2.
Усно виконай вправу 289, стор. 59 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи, стор. 59 підручника: 291; 293; 295 (3, 4).
Завдання 4.
Виконай письмово вправи, стор. 59 – 60 підручника: 299, 300.
Завдання 5.
Виконай письмово вправи, стор. 60 підручника: 301; 302.

Готуємось до індивідуального опрацювання
-
Обчисли:
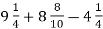 .
.
-
Розв’яжи рівняння:
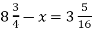 .
.
-
Обчисли:
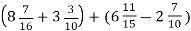 .
.
-
Довжина картини дорівнює
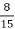 м, а ширина –
м, а ширина – 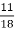 м. Що більше: довжина чи ширина і на скільки?
м. Що більше: довжина чи ширина і на скільки?
Урок №17
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Звичайні дроби. Додавання і віднімання звичайних дробів
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 2.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Який із дробів дорівнює
 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Вибери корінь рівняння
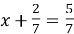 .
.
|
А |
Б |
В |
Г |
|
|
5 |
|
1 |
-
Обчисли:
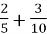 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Що більше
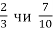 ?
?
-
Обчисли: 1)
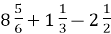 ; 2)
; 2) 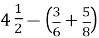 .
.
-
Від мотка дроту завдовжки 50 м відрізали
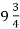 м, а потім ще
м, а потім ще 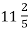 м. Скільки метрів дроту залишилось у мотку?
м. Скільки метрів дроту залишилось у мотку?
-
Розв’яжи рівняння:
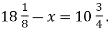
- Одна бригада робітників може виконати певну роботу за 4 год, а друга – за 6 год. Яка частина роботи залишиться невиконаною після спільної роботи двох бригад впродовж 1 год?
-
Два брати, в яких було порівну грошей, купили книги. Старший брат витратив
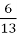 своїх грошей, а молодший –
своїх грошей, а молодший – 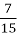 своїх. У кого з них залишилось більше грошей?
своїх. У кого з них залишилось більше грошей?
Тема №3.Множення і ділення звичайних дробів
Урок №1

Множення і ділення звичайних дробів
Математика – це спосіб називати
різні речі одним ім’ям.
А. Пуанкаре
Питання
- Множення звичайних дробів
- Знаходження дробу від числа
- Взаємно обернені числа
- Ділення звичайних дробів. Знаходження числа за його дробом
Література
Істер О.С. Математика: підручник для 6 класу, Київ: «Генеза», 2014. – параграф 14 – 19, стор. 61 – 93
|
1. Множення звичайних дробів |
|||
|
1.1 |
Щоб помножити дріб на натуральне число, треба помножити на це число його чисельник, а знаменник залишити без зміни. |
|
|
|
1.2 |
Добутком двох дробів є дріб, чисельник якого дорівнює добутку чисельників, а знаменник – добутку знаменників цих дробів. |
|
|
|
1.3 |
Щоб помножити мішані числа, треба спочатку записати їх у вигляді неправильних дробів, а потім скористатись правилом множення дробів. |
|
|
|
1.4 |
Властивості множення a ∙ b = b ∙ a – переставна a ∙ (b ∙ c) = (a ∙ b) ∙ c – сполучна
a ∙ (b
|
||
|
2. Знаходження дробу від числа |
|||
|
2.5 |
Щоб знайти дріб від числа, треба це число помножити на дріб.
|
У саду росте 36 дерев. З них
|
|
|
2.6 |
Щоб знайти відсотки від числа, можна подати відсотки у вигляді дробу і помножити число на цей дріб. |
Полуниці містять в середньому 6% цукру. Скільки цукру міститься у 15кг полуниць? 6% = 0,06; 15 ∙ 0,06 = 0,9 (кг) – цукру в цих полуницях. |
|
|
3. Взаємно обернені числа |
|||
|
3.7 |
Два числа, добуток яких дорівнює 1 називаються взаємно оберненими. |
|
|
|
3.8 |
Число, обернене до 1, є саме число 1. Числу 0 оберненого числа не існує. |
||
|
3.9 |
Якщо потрібно знайти число, обернене до мішаного числа, або до десяткового дробу, або до натурального числа, то потрібно спочатку записати їх у вигляді звичайного дробу, а потім шукати обернені числа. |
|
|
|
4. Ділення звичайних дробів. Знаходження числа за його дробом |
|||
|
4.10 |
Щоб поділити два дроби, треба ділене помножити на число, обернене до дільника.
|
|
|
|
4.11 |
Властивості ділення:
1) 3) На нуль ділити не можна! |
0: |
|
|
4.12 |
Щоб знайти число за значенням його дробу, можна це значення поділити на цей дріб.
|
Знайти число,
48 : |
|
|
4.13 |
Щоб знайти число за його відсотками, необхідно ці відсотки подати у вигляді дробу і поділити значення відсотків на цей дріб.
|
Знайти число, 50% якого дорівнюють 42. 50% = 0,5; 42 : 0,5 = 84. |
|
Урок №2
«Хороші друзі дістаються тому,
хто сам уміє бути хорошим другом»
Ніколо Макіавеллі
Фронтальне опрацювання матеріалу
Множення звичайних дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.4 блоку № 3.
- Усно дай відповіді на питання:
- Як помножити число на звичайний дріб?
- Що називають добутком двох дробів?
- Як перемножити мішані числа?
- Сформулюй властивості множення дробів.
Завдання 2.
Усно розв’яжи вправу 304, стор. 63 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи стор. 64 підручника: 305 (1, 3, 5, 7, 9, 11); 307.
Завдання 4.
Письмово виконай вправи, запропоновані вчителем у практичній роботі.
Завдання 5.
Письмово виконай вправи стор. 66 – 67 підручника: 327; 336; 337.
Уроки №3, 4
«Скільки зла таїться всередині
за гарною подобою: гадюка ховається в траві»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Знаходження дробу від числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1. – 2.6 блоку № 3.
- Встав пропущені слова чи словосполучення:
-

 Щоб помножити мішані числа, потрібно спочатку записати їх у вигляді
Щоб помножити мішані числа, потрібно спочатку записати їх у вигляді  , а потім
, а потім  .
.
- Добутком двох дробів є дріб, чисельник якого дорівнює , а знаменник –
-
Щоб помножити дріб на натуральне число, треба
 , а знаменник
, а знаменник  .
.
-
Щоб знайти дріб від числа, треба
 .
.
-
Щоб знайти відсотки від числа, можна
 і помножити
і помножити  .
.
Завдання 2.
Виконай усно вправу 343, стор. 69 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 70 підручника: 344, 346.
Завдання 4.
Прослухай казку про царя Бум-Бума і виконай завдання, запропоноване вчителем.
Завдання 5.
Письмово розв’яжи вправи, стор. 70 підручника: 348; 349.
Завдання 6.
Письмово розв’яжи вправи, стор. 70 – 71 підручника: 351; 352.
Завдання 7.
Розв’яжи вправи:
-
На шкільній виставці 72 малюнки.
 всіх малюнків написано аквареллю, а 25 % решти – олівцем. Скільки на виставці малюнків, виконаних олівцем?
всіх малюнків написано аквареллю, а 25 % решти – олівцем. Скільки на виставці малюнків, виконаних олівцем?
-
Музиканти вирішили підготувати до свого концерту 24 номери. За перший місяць було підготовлено
 всієї програми, а другого місяця –
всієї програми, а другого місяця –  всієї програми. Скільки номерів ще залишилось підготувати?
всієї програми. Скільки номерів ще залишилось підготувати?
-
Довжина екватора Землі приблизно 40 000 км, а її діаметр складає
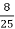 довжини екватора. Чому дорівнює діаметр Землі?
довжини екватора. Чому дорівнює діаметр Землі?
-
Маса мурашки складає 10 % маси вантажу, який вона може перенести за 1 раз. Яка маса мурашки, якщо за 1 раз вона може перенести
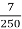 г вантажу?
г вантажу?
-
Дмитрик йде зі швидкістю
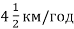 , а швидкість Ігоря складає
, а швидкість Ігоря складає  швидкості Дмитрика. Через який час відстань між хлопчиками буде 3 км?
швидкості Дмитрика. Через який час відстань між хлопчиками буде 3 км?
Урок №5
«І все, що тільки робите словом чи ділом, усе робіть
у Ім'я Господа Ісуса, дякуючи через Нього Богові й Отцеві»
1Послання апостола Павла до Колосян 3:17
Фронтальне опрацювання матеріалу
Взаємно обернені числа
І. Робота над засвоєнням понять термінів і правил
Завдання 1.
- Повтори тези 1.1. – 3.9 блоку № 3.
- Постав у відповідність поняттю чи правилу його продовження:
- Щоб помножити дріб на натуральне число, треба …
- Добутком двох дробів є дріб …
- Щоб знайти дріб від числа, треба …
- Взаємно обернені числа – це числа …
- Якщо потрібно знайти число, обернене до мішаного числа або до десяткового дробу, або до натурального числа, то потрібно …
- Назвіть число, обернене до 1.
- Щоб знайти відсотки від числа, можна …
- Щоб помножити мішані числа, треба …
А) це число помножити на дріб.
Б) добуток яких дорівнює 1.
В) помножити на це число його чисельник, а знаменник залишити без змін.
Г) чисельник якого дорівнює добутку чисельників, а знаменник – добутку знаменників цих дробів.
Д) саме число 1.
Е) подати відсотки у вигляді дробу і помножити число на цей дріб.
Є) спочатку записати їх у вигляді звичайного дробу, а потім шукати обернені числа.
Ж)спочатку записати їх у вигляді неправильних дробів, а потім скористатись правилом множення дробів.
Завдання 2.
-
Назви числа, обернені до:
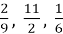 ; 2; 0,1.
; 2; 0,1.
- Чи існує число, обернене нулю?
Завдання 3.
Переглянь приклади 1, 2, 3, стор. 73 – 74 підручника. Використай їх як зразки для розв’язування письмових завдань.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
- Виконай письмово вправи, стор. 74 – 75 підручника: 377, 381, 383, 385; 387; 388.
-
Обчисли значення виразу найзручнішим способом:
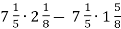 .
.

Готуємось до індивідуального опрацювання
-
Обчисли: 1)
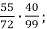 2)
2) 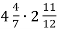 .
.
-
 Який шлях проїде поїзд за
Який шлях проїде поїзд за  год, якщо його швидкість дорівнює 36 км/год?
год, якщо його швидкість дорівнює 36 км/год?
-
До магазину завезли 180 кг капусти. За перший день було продано
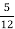 завезеної капусти. Скільки кг капусти було продано за перший день?
завезеної капусти. Скільки кг капусти було продано за перший день?
-
Обчисліть значення виразу найзручнішим способом:
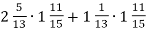 .
.
-
За три дні продали 120 кг олії. Першого дня продали
 усієї олії, другого -
усієї олії, другого - 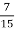 решти. Скільки кг олії продали третього дня?
решти. Скільки кг олії продали третього дня?
Уроки №7 – 9
«Я все роблю для Бога»
Мати Тереза
Фронтальне опрацювання матеріалу
Ділення звичайних дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1. – 4.11.
- Усно дай відповідь на питання:
- Як поділити два дроби?
- Якщо 1 поділити на дріб, то отримаємо…
- Які два числа називаються взаємно оберненими?
- Як помножити мішані числа?
- Що називають добутком двох дробів?
- Як знати дріб від числа?
- На яке число ділити не можна?
- Якщо нуль поділити на дріб, то що отримаємо…
- Як знайти число, обернене до мішаного числа, або до десяткового дробу, або до натурального числа?
- Як знайти відсотки від числа?
- Як помножити дріб на натуральне число?
Завдання 2.
Розглянь приклади розв’язування вправ:
-
Знайди частку:
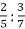 .
.
![]() .
.
-
Знайди частку:
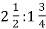 .
.
![]() .
.
-
Знайди частку:
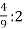 .
.
![]() .
.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
3.1. Виконай письмово вправи, стор. 77 – 79 підручника: 394, 412, 414 (2)
3.2. Виконай письмово:
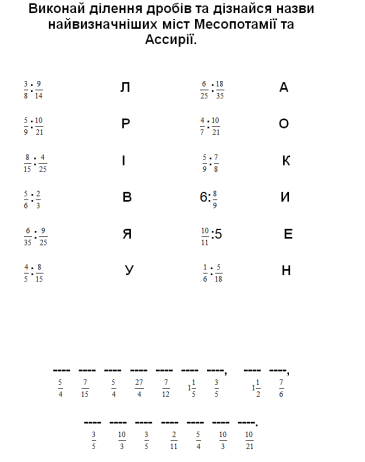
Завдання 4.
Виконай письмово вправу 419, стор. 80 підручника.
Завдання 5.
-
Смажене м'ясо перетравлюється 5 год в організмі людини. Визначте час перетравлювання молока, грибів, хліба, салату, якщо від дорівнює відповідно
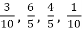 часу, що потрібен на перетравлювання смаженого м’яса.
часу, що потрібен на перетравлювання смаженого м’яса.

-
Профілактичні щеплення – єдиний засіб попередження дифтерії (хвороби, що уражає ротоглотку та дихальні шляхи). У класі щеплення від дифтерії зроблені всім 25 учням. Це складає
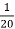 всіх учнів школи. Знайдіть кількість нещеплених дітей, якщо їх частина складає 0,02.
всіх учнів школи. Знайдіть кількість нещеплених дітей, якщо їх частина складає 0,02.
-
Добовий раціон дорослої людини має містити
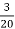 частини білків,
частини білків, 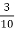 – жирів і
– жирів і 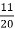 – вуглеводів. Виразіть ці складові у відсотках.
– вуглеводів. Виразіть ці складові у відсотках.
Завдання 6.
 Іван Якович Франко — видатний український письменник, поет, публіцист, перекладач, учений, громадський і політичний діяч. Доктор філософії (1893), дійсний член Наукового товариства імені Шевченка (1899), почесний доктор Харківського університету (1906).
Іван Якович Франко — видатний український письменник, поет, публіцист, перекладач, учений, громадський і політичний діяч. Доктор філософії (1893), дійсний член Наукового товариства імені Шевченка (1899), почесний доктор Харківського університету (1906).
- Виконай наступні завдання і ти дізнаєшся дату народження українського письменника Івана Франка:
1) 2% від числа 100
2) половина якого числа дорівнює 3,5?
3) ![]()
4) ![]() .
.
5) ![]() .
.
6) ![]() від 24.
від 24.
7) ![]() .
.
8) ![]() .
.
- Розв’язавши задачу, ти дізнаєшся скільки мов знав Іван Франко.
Нині у світі налічується 5000 мов і діалектів. Мови, що зникли становлять 28% від цієї кількості. Кількість іноземних мов, які знав Іван Франко, становить 0,01 від кількості мов, що зникли. ![]()
- Розв’язавши рівняння, ти дізнаєшся скільки казок написав Іван Франко.
![]() .
.
Якщо число, що дорівнює 50% кореня рівняння, помножити на 25, то одержимо кількість казок, яку написав Іван Франко.
- Розв’язавши задачу, ти дізнаєшся у скількох томах можна видати всі твори Івана Франка.
Іван Якович Франко написав 6000 творів. Кількість виданих томів становить ![]() усіх творів, а це 50% тих томів, що можна видати. У скількох томах можна видати всі твори Великого Каменяра?
усіх творів, а це 50% тих томів, що можна видати. У скількох томах можна видати всі твори Великого Каменяра?
Уроки №10, 11
«Біблія — це найкращий дар, даний людині Богом.
Через цю книгу Спаситель світу звістив усі блага.
Без неї ми не могли б розпізнати істину та неправду»
Авраам Лінкольн
Фронтальне опрацювання матеріалу
Знаходження числа за його дробом
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези блоку №3.
- Дай відповіді на питання. Якщо ти правильно виконаєш завдання, то зможеш відкрити захований малюнок:
- Як знайти число за значенням його дробу?
- Що називають добутком двох дробів?
- Як знайти число за його відсотками?
- Як поділити два дроби?
- Які числа називаються взаємно оберненими?
- Як помножити мішані числа?
- До якого числа немає оберненого йому числа?
- Як знайти дріб від числа?
- Як помножити натуральне число на дріб?
Завдання 2.
Усно виконай вправи:
-
Розглянь приклад розв’язування задачі: Лижник пройшов 300 м, що становить
 всієї дистанції. Яка довжина всієї дистанції?
всієї дистанції. Яка довжина всієї дистанції?
![]() (м) – довжина дистанції.
(м) – довжина дистанції.
-
Користуючись розглянутим прикладом, виконай вправу: Відремонтували 90 км дороги, що становить
 всієї дороги. Яка довжина дороги?
всієї дороги. Яка довжина дороги?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи:
-
Паля здіймається над водою на 1,5 м, що становить
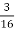 довжини всієї палі. Яка довжина всієї палі?
довжини всієї палі. Яка довжина всієї палі?
-
Стовп, закопаний в землю на
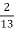 своєї довжини, здіймається над землею на
своєї довжини, здіймається над землею на 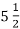 м. Знайди всю довжину стовпа.
м. Знайди всю довжину стовпа.
-
Після того, як туристи пройшли
 всього шляху, їм залишилось пройти 28 км. Яка довжина їх маршруту?
всього шляху, їм залишилось пройти 28 км. Яка довжина їх маршруту?
-
Маса винограду в першому ящику становить
 маси винограду в другому ящику. Скільки кілограмів винограду було в обох ящиках, якщо в першому ящику 21 кг винограду?
маси винограду в другому ящику. Скільки кілограмів винограду було в обох ящиках, якщо в першому ящику 21 кг винограду?
- Під час сушіння картопля втрачає 85,7% своєї маси. Скільки потрібно взяти свіжої картоплі, щоб отримати 71,5 т сушеної?
- Магазин за перший день продав 40% всіх зошитів, за другий день – 53% всіх зошитів, за третій –847 зошитів. Скільки зошитів продав магазин за три дні?
-
Доповідь учня становить
 уроку, розповідь вчителя
уроку, розповідь вчителя 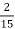 , а розв’язування задач –
, а розв’язування задач –  уроку. Решту уроку учні писали самостійну роботу. Скільки хвилин тривала самостійна робота, якщо тривалість уроку 45 хвилин?
уроку. Решту уроку учні писали самостійну роботу. Скільки хвилин тривала самостійна робота, якщо тривалість уроку 45 хвилин?
- Коли Костя пройшов 0,3 всього шляху від дому до школи, йому ще залишилось пройти до середини шляху 150 м. Якої довжини шлях від дому Кості до школи?
- Спортивний майданчик, площею 420 м2, займає 7% шкільної ділянки. Яка площа шкільної ділянки?
-
Із села в місто одночасно в одному напрямку виїхали велосипедист і мотоцикліст. Швидкість велосипедиста 15 км/год, що становить
 швидкості мотоцикліста. Яка відстань буде між ними через 36 хв після виїзду?
швидкості мотоцикліста. Яка відстань буде між ними через 36 хв після виїзду?
-
Андрій важить 16 кг, що становить
 ваги його старшої сестри і
ваги його старшої сестри і  ваги його тата. Вага мами становить
ваги його тата. Вага мами становить  ваги тата. Чи зможуть вони всі разом піднятися на ліфті, вантажопідйомністю 300 кг, якщо з ними повинен піднятися їхній собака, який важить 17 кг?
ваги тата. Чи зможуть вони всі разом піднятися на ліфті, вантажопідйомністю 300 кг, якщо з ними повинен піднятися їхній собака, який важить 17 кг?

Готуємось до індивідуального опрацювання
-
 Розв’яжи рівняння
Розв’яжи рівняння 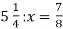 .
.
-
З якою швидкістю повинен їхати автомобіль, щоб проїхати
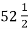 км за
км за  год?
год?
-
У саду росте 35 вишень, що становить
 всіх дерев, які ростуть у саду. Скільки дерев у саду?
всіх дерев, які ростуть у саду. Скільки дерев у саду?
-
До санаторії завезли апельсини, мандарини і лимони. Маса апельсинів становила
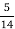 всіх фруктів, маса мандаринів -
всіх фруктів, маса мандаринів - 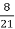 , а лимонів – решту 99 кг. Скільки кілограмів фруктів завезли до санаторію?
, а лимонів – решту 99 кг. Скільки кілограмів фруктів завезли до санаторію?
Уроки №13, 14
«Я приписую Біблії велич Англії»
Королева Вікторія
Фронтальне опрацювання матеріалу
Розв’язування вправ на всі дії зі звичайними та десятковими дробами
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок №3.
- Усно дай відповіді на питання:
- Що називають добутком двох дробів?
- Як помножити десяткові дроби?
- Як поділити звичайні дроби?
- Як знайти дріб і відсоток від числа?
- Як помножити десятковий дріб на 10, 100, 1000 і т.д.?
- Що називають взаємно оберненими числами?
- На яке число не можна ділити?
- Сформулюй переставну властивість додавання і множення.
- Як помножити мішані числа?
- Як додати або відняти дроби з різними знаменниками?
- Як порівняти дроби з різними знаменниками?
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 2.
Математика – королева наук. Вона має зв’язки з багатьма науками. Розв’яжіть завдання, запропоновані вчителем, які поєднанні зі шкільними предметами, і ви дізнаєтесь назву природного явища, яке будете вивчати у курсі фізики.
-
Іван Франко прожив у Львові 40 років, що становить
 його життя. Скільки років прожив письменник?
його життя. Скільки років прожив письменник?
-
Великий Каменяр
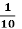 частину свого життя провів у рідному селі Нагуєвичі. Скільки років прожив Іван Якович у батьківському домі?
частину свого життя провів у рідному селі Нагуєвичі. Скільки років прожив Іван Якович у батьківському домі?
- До першого австрійського парламенту українці обрали 35 чоловік. Серед них: 60% – селяни, 20% – священики, а решта – інтелігенція. Скільки представників інтелігенції було серед українських парламентарів?
-
Коли готують пюре зі слив,
 частина їх іде у відходи. Скільки треба взяти слив, щоб приготувати 5 кг пюре?
частина їх іде у відходи. Скільки треба взяти слив, щоб приготувати 5 кг пюре?
-
Із 640 найважливіших культурних рослин земної кулі
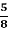 походять із Азії,
походять із Азії, 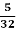 – з Північної та Південної Америки, а
– з Північної та Південної Америки, а 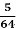 – з Африки. Скільки культурних рослин походять з інших частин світу?
– з Африки. Скільки культурних рослин походять з інших частин світу?
-
Маса мозку дорослої людини приблизно 1400 г, а маса мозку семирічної дитини становить
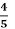 від маси мозку дорослої людини. Яка приблизна маса мозку семирічної дитини?
від маси мозку дорослої людини. Яка приблизна маса мозку семирічної дитини?
- Мідна руда містить 85 % міді. Скільки міді міститься у 260 т такої мідної руди?
-
Довжина прямокутника дорівнює 108 см, що становить
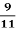 його ширини. Знайди периметр трикутника.
його ширини. Знайди периметр трикутника.
Завдання 3.
Математичний диктант «Будівельник».
Ви повинні на кожне із запитань вибрати правильну відповідь та записати її номер у знаменники відповідних дробів.
Питання.
- Число, записане над рискою дробу називають …
- Якщо чисельник і знаменник дробу є взаємно простими числами, то дріб є …
- Дріб, у якого чисельник більший від знаменника, називається …
- Риску дробу можна розглядати як знак …
- З двох дробів з однаковими знаменниками більшим є той, у якого чисельник …
- Число, яке показує на скільки рівних частин поділили якесь ціле називається …
Відповіді.
- Більший
- Правильний
- Знаменник
- Множення
- Чисельник
- Неправильний
- Ділення
- Додавання
- Нескоротний
- Менший
- Період
- Скоротний
Завдання 4.
 Задача вчителя біології
Задача вчителя біології
-
Середня маса шестикласника становить 36 кг. Кров становить
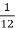 маси тіла дитини, а
маси тіла дитини, а  всієї крові міститься в кровоносних судинах. Яка кількість крові знаходиться у судинах?
всієї крові міститься в кровоносних судинах. Яка кількість крові знаходиться у судинах?
Задача вчителя географії
- Площа суходолу на земній кулі приблизно дорівнює 150 млн. км2. Південна Америка займає 12%, а Африка – 20% суходолу. Яка площа вказаних материків?
Задача вчителя музики
-
 Знайдіть ноту, якої не вистачає.
Знайдіть ноту, якої не вистачає.
Виконай письмово вправи, стор.88 – 90 підручника: 468 (1, 3), 476 (1), 486.

Готуємось до індивідуального опрацювання
-
Михайлик прочитав
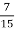 книжки, у якій 300 сторінок. Скільки сторінок прочитав Михайлик?
книжки, у якій 300 сторінок. Скільки сторінок прочитав Михайлик?
-
Обчисли:
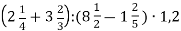 .
.
-
Для учнів класу купили зошити, ручки та олівці. Вартість зошитів становила
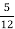 вартості всієї покупки, вартість ручок -
вартості всієї покупки, вартість ручок -  , а вартість олівців – решту 70 грн. Знайдіть вартість усієї покупки.
, а вартість олівців – решту 70 грн. Знайдіть вартість усієї покупки.
Урок №16
«Мудрість краща від зброї військової»
Книга Еклезіаста 9:18
Внутрішньопредметне узагальнення матеріалу
Множення і ділення звичайних дробів
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок №3.
- Письмово дай відповіді на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
Обчисли:
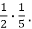
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайди значення частки
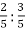 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Перетвори звичайний дріб
 у десятковий.
у десятковий.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
Обчисли: а)
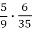 ; б)
; б) 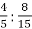 .
.
-
У книжці 210 сторінок. Учень прочитав
 усієї книжки. Скільки сторінок прочитав учень?
усієї книжки. Скільки сторінок прочитав учень?
-
Обчисли:
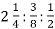 .
.
-
У саду росло 500 дерев. Яблуні становили
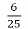 всіх дерев, вишні –
всіх дерев, вишні – 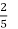 дерев, а сливи – решту. Скільки слив росло в саду?
дерев, а сливи – решту. Скільки слив росло в саду?
-
Розв’яжи рівняння:
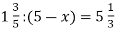 .
.
Тема №4. Відношення і пропорції
Урок №1

Відношення і пропорції
«Не будь переможений
злом, але перемагай зло добром»
Послання ап. Павла до римлян, 12:21
Питання
- Відношення.
- Пропорції.
- Пряма і обернена пропорційна залежність. Масштаб
- Поділ числа у даному відношенні.
- Відсоткове відношення двох чисел.
Література
Істер О.С. Математика: підручник для 6 класу, Київ: «Генеза», 2014. – §§ 20 – 24, 27, 28; стор. 94 – 117, 131 – 140.
|
1. Відношення |
||
|
1.1 |
Частку двох чисел називають відношенням цих чисел. |
а : b, а і b – члени відношення 3 : 4; 0,5 : 1,2 |
|
1.2 |
Відношення показує, у скільки разів перше число більше за друге або яку частину перше число складає від другого. |
|
|
1.3 |
Основна властивість відношення Відношення двох чисел не зміниться, якщо кожне із чисел відношення помножити або поділити на одне й те саме, відмінне від нуля, число. |
1 : 2 = 5 : 10 25 : 15 = 5 : 3 |
|
2. Пропорції |
||
|
2.4 |
Рівність двох відношень називають пропорцією.
b, c – середні члени пропорції |
2 : 5 = 6 : 15 2, 15 – крайні члени пропорції; 5, 6 – середні члени пропорції |
|
2.5 |
Основна властивість пропорції
Добуток крайніх членів пропорції дорівнює добутку її середніх членів: |
2 : 5 = 6 : 15 2 ∙ 15 = 5 ∙ 6 |
|
2.6 |
Середні члени пропорції або (та) крайні члени пропорції можна міняти місцями. |
2 : 5 = 6 : 15
|
|
3. Пряма і обернена пропорційна залежність. Масштаб |
||
|
3.7 |
Дві величини, відношення відповідних значень яких є сталим, називають прямо пропорційними.
|
а – сторона квадрата,
Р – периметр квадрата |
|
3.8 |
Зі збільшенням (зменшенням) значень однієї з прямо пропорційних величин у кілька разів значення другої величини збільшується (зменшується) у стільки ж разів. |
Швидкість і шлях, пройдений за той самий час; сторона квадрата і його периметр |
|
3.9 |
Дві змінні величини називають обернено пропорційними, якщо при збільшенні (зменшенні) однієї із них друга зменшується (збільшується) у стільки ж разів. |
|
|
3.10 |
Відношення довжини відрізка на карті до довжини відрізка на місцевості називають масштабом карти. |
|
|
4. Поділ числа у даному відношенні |
||
|
4.11 |
Для приготування тіста для млинців необхідно взяти борошно, молоко й олію у відношенні 8 : 5 : 1 (8 мірок борошна, 5 мірок молока, 1 мірку олії). Скільки грамів борошна треба взяти, щоб отримати 840г тіста? І спосіб 1) 8 + 5 + 1 = 14 (частин) – становить все тісто; 2) 840 : 14 = 60 (г) – припадає на одну частину; 3) 60 ∙ 8 = 480 (г) – потрібно взяти борошна. ІІ спосіб
14х = 840; х = 840 : 14; х = 60 (г) – становить одна частина; 2) 60 ∙ 8 = 480 (г) – потрібно взяти борошна. Відповідь: 480г.
|
|
|
5. Відсоткове відношення двох чисел |
||
|
5.12 |
Відсоткове відношення двох чисел – це їх відношення виражене у відсотках. |
|
|
5.13 |
Відсоткове відношення показує, скільки відсотків одне число становить від другого. |
|
|
5.14 |
Щоб знайти відсоткове відношення двох чисел, треба знайти їх відношення і помножити його на 100%. |
Скільки відсотків складає 1га від 5га? 1 : 5 = 0,2 = 20% |
|
5.15 |
Щоб дізнатись скільки відсотків одне число складає від іншого, достатньо перше число поділити на друге і знайдену частку помножити на 100 %. |
У класі 20 учнів, з них 14 відвідали театр. Скільки відсотків від учнів класу відвідали театр?
|
|
5.16 |
Щоб знайти на скільки відсотків змінилась величина, необхідно знайти: 1) на скільки одиниць змінилась ця величина; 2) скільки відсотків становить знайдена різниця від початкового значення величини. |
Вартість товару зросла зі 150 грн. до 240 грн. На скільки відсотків збільшилась ціна? 1) 240 – 150 = 90 (грн.)
2) |
Урок №2
«Потрібно кожному змінювати щось у собі. Якщо
ти станеш іншим, і навколо тебе мільйон людей
стануть іншими, то і країна почне змінюватись»
Святослав Вакарчук
Фронтальне опрацювання матеріалу
Відношення. Основна властивість відношення
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3. блоку №4.
- Дай усно відповіді на питання:
- Що називається відношенням?
- Чи можна частку 42 м : 14 назвати відношенням?
- Яким відношенням менших чисел можна замінити відношення чисел 700 : 300?
- Сформулюй основну властивість відношення.
- Знайди відношення чисел 20 : 5; 36 : 12; 8,1 : 0,9.
Завдання 2.
Розглянь приклад розв’язування вправи:
В акваріум, який вміщає 12 л води, налили 10 л. Яка частина акваріума не заповнена?
-
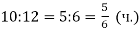 – на стільки заповнений акваріум;
– на стільки заповнений акваріум;
-
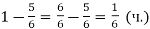 – акваріума не заповнена.
– акваріума не заповнена.
Відповідь: ![]() частина.
частина.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи:
- Для варення на 3,5 кг ягід було взято 4,2 кг цукру. В якому відношенні були взяті ягоди і цукор?
- Відстань від села до міста автомашина пройшла за три години. За першу годину вона пройшла чверть всієї відстані, за другу годину – третину всієї відстані. У скільки разів відстань, пройдена за третю годину, більша відстані, пройденої за другу годину? Яку частину відстань, пройдена за першу годину, складає від відстані, пройденої за третю годину?
- В клавішах піаніно на кожні 7 білих клавіш припадає 5 чорних. Разом вони складають октаву. Яку частину октави складають білі клавіші?
- Зі 100 виготовлених телевізорів 20 виявились поламані. Яку частину складають телевізори в робочому стані?
- Сергій і Дмитро змагались, хто краще кидає м’яч у кільце. Сергій із 20 кидків попав в кільце 15 разів. Дмитро із 30 кидків попав 18 разів. У кого із них кращий результат?
-
Восени з трьох яблунь зібрали врожай 90 кг яблук. З першої яблуні зібрали 35 кг, з другої –
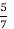 врожаю першої яблуні. З якої яблуні зібрали більше яблук – з другої чи з третьої, і на скільки? Яку частину всього врожаю складають яблука, зібрані з третьої яблуні?
врожаю першої яблуні. З якої яблуні зібрали більше яблук – з другої чи з третьої, і на скільки? Яку частину всього врожаю складають яблука, зібрані з третьої яблуні?
Урок №3
Фронтальне опрацювання матеріалу
Відношення. Основна властивість відношення
Виконати роботу у практичному зошиті «Я дослідник», тема 2.
Урок №4

Фронтальне опрацювання матеріалу
Пропорція. Основна властивість пропорції
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1. – 2.6 блоку № 4.
- Дай відповіді на питання:
- Що називають пропорцією?
- Як називають числа, з яких складається пропорція?
- Сформулювати основну властивість пропорції.
- Що таке відношення?
- Сформулювати основну властивість відношення.
- Замініть синонімами слово «відношення».
Завдання 2.
1)Як прочитати запис: 1:3=2:6?
2)Чому дорівнює добуток крайніх членів?
3)Чому дорівнює добуток середніх членів?
Завдання 3.
- Перегляньте презентацію, запропоновану вчителем.
- Розв’яжи усно вправи, стор. 100 підручника: 527, 528, 529.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
- Письмово виконай вправи стор. 101 – 102 підручника: 530, 538, 540.
- Самостійно, розбившись на групи за партами, виконайте наступну роботу:
- Проаналізуй подані пропорції. Доповни висловлювання.
![]()
![]()
Крайні члени пропорції:
Середні члени пропорції:
Крайні члени пропорції:
Середні члени пропорції:
Добуток крайніх членів пропорції:
![]()
Добуток крайніх членів пропорції:
![]()
Добуток середніх членів пропорції:
![]()
Добуток середніх членів пропорції:
![]()
- Порівняй результати обчислень і перевір, чи вірна основна властивість пропорції.
- Перевір, чи справджується ця властивість для інших пропорцій
![]()
![]()
Урок №5
Фронтальне опрацювання матеріалу
Пропорція. Основна властивість пропорції
Виконати роботу у практичному зошиті «Я дослідник», тема 4.
Урок №6
«Для всього свій час, і година своя кожній справі під небом»
Книга Еклезіаста 3:1
Фронтальне опрацювання матеріалу
Пряма і обернена пропорційна залежність
І. Робота із засвоєння понять, термінів і правил
Завдання 1.
- Повтори тези 1.1. – 3.9 блоку № 4.
- Дай відповіді на питання:
- Що називають пропорцією?
- Як називають числа, з яких складається пропорція?
- Сформулювати основну властивість пропорції.
- Які величини називають прямо пропорційними?
- Яку властивість мають прямо пропорційні величини?
- Які величини називають обернено пропорційними?
- Що таке відношення?
-
Сформулювати основну властивість відношення.
- Визнач, чи є прямо пропорційними величини:
- Довжина сторони квадрата та його периметр
- Швидкість автомобіля і відстань, яку проїде він за певний час.
- Вік дерева та його висота
- Вартість товару купленого по одній ціні і його кількість.
Завдання 2.
Розглянь розв’язування задачі, стор. 104 підручника.
Як розв’язують задачі на прямо пропорційні величини?
Завдання 3.
Усно виконай вправи, стор. 105 підручника: 555; 557; 558.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
Письмово виконай вправи, стор. 106 підручника:
562; 568 – колективно;
565 – самостійно.
Завдання 5.
Письмово виконай вправи, стор. 130 підручника: 678.
Завдання 6.
За призначенням лікаря хворий купив в аптеці сироп проти кашлю. На пляшці зазначено: «30мг/5мг». Це означає, що в 5 мг цього сиропу міститься 30 мг лікувальної речовини. За інструкцією, кількість лікувальної речовини на один прийом не повинна перевищувати 180 мг. Скільки мілілітрів сиропу може прийняти хворий за один раз?
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних вправ
Завдання 7.
Письмово виконай вправу 684, стор. 130 підручника.
Урок №7
«Світ – це книжка, і той, хто
не подорожує, читає лише одну сторінку»
Св. Августин
Фронтальне опрацювання матеріалу
Масштаб. Знаходження відстаней на карті
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.10 блоку № 4.
- Усно дай відповіді на питання:
- Що називають відношенням?
- Як перевірити чи правильна пропорція?
- Сформулюй основну властивість відношення.
- Які величини називають прямо пропорційними?
- Які величини називають обернено пропорційними?
- Яку властивість мають прямо пропорційні величини?
- Дай означення масштабу.
Завдання 2.
2.1. Запиши в блок співвідношення для швидкого знаходження масштабу:
![]()
2.2. Відгадайте ребус
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Виконати роботу у практичному зошиті «Я дослідник», тема 3.
Урок №8
«…бо мудрість увійде до серця твого,
і буде приємне знання для твоєї душі!»
Книга приповістей Соломонових 2:10
Фронтальне опрацювання матеріалу
Поділ числа у даному відношенні
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 4.11 блоку № 4.
- Усно дай відповіді на питання:
- Що таке відношення?
- Що таке пропорція?
- Сформулюй основну властивість відношення.
- Які величини називаються прямо і обернено пропорційними?
- Сформулюй основну властивість пропорції.
- Дай визначення масштабу.
- Які є способи розв’язування задач на поділ числа у даному відношенні?
Завдання 2.
- Розглянь розв’язання задачі 1 та задачі 2, стор. 114 – 115 підручника.
- Користуючись розглянутими прикладами, виконай усно вправу 620, стор. 115 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 116 підручника: 622 (1); 626.
Завдання 4.
Розв’яжи задачі другим способом:
- Троє поросят Ніф-Ніф, Наф-Наф та Нуф-Нуф взялися обробити поле цукрових буряків. Ніф-Ніф обробив 50 рядків, Наф-Наф обробив 30 рядків, а Нуф-Нуф обробив 10 рядків. За обробку поля вони заробили 1 800 гривень. Як ці гроші треба поділити між поросятами?
- Периметр трикутника дорівнює 140 см, а його сторони відносяться як 8:12:15. Знайдіть сторони трикутника.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 5.
Щоб приготувати шашлик, зазвичай купують м'ясо з розрахунку 300 г на одну людину. Для маринаду беруть (на 2 кг свинини): 1 лимон, 3 цибулини, 4 столових ложки рослинної олії та спеції за смаком. Скільки м’яса, лимонів, цибулі й олії потрібно купити для маринування м’яса на шашлик для компанії з 6 осіб?


Готуємось до індивідуального опрацювання
-
Заміни відношення дробових чисел відношенням натуральних чисел
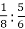 .
.
-
Чи правильна пропорція
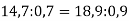 ?
?
-
Розв’яжи рівняння:
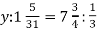 .
.
- Відстань між двома пунктами на карті дорівнює 3,2см. Яка відстань між цими пунктами на місцевості, якщо масштаб карти 1 : 500 000?
- У 400 кг сплаву міститься 176кг міді. Скільки кг міді міститься у 325 кг сплаву?
- Периметр трикутника дорівнює 140 см, а його сторони відносяться як 8:12:15. Знайдіть сторони трикутника.
Уроки №10, 11
«…бо мудрість увійде до серця твого,
і буде приємне знання для твоєї душі!»
Книга приповістей Соломонових 2:10
Фронтальне опрацювання матеріалу
Відсоткове відношення двох чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 5.14 блоку № 4.
- Усно дай відповіді на питання:
- Що таке відношення?
- Що таке пропорція?
- Сформулюй основну властивість відношення.
- Які величини називаються прямо пропорційними?
- Сформулюй основну властивість пропорції.
- Дай визначення масштабу.
- Які є способи розв’язування задач на поділ числа у даному відношенні?
- Що називають відсотком?
- Що таке відсоткове відношення двох чисел?
- Що показує відсоткове відношення чисел?
- Як знайти відсоткове відношення двох чисел?
- Як дізнатись скільки відсотків одне число складає від другого?
Завдання 2.
- Розглянь розв’язання задачі 1 та 2, стор. 132 підручника.
- Користуючись розглянутими прикладами, виконай усно вправи 691; 692 стор. 133 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 133 - 134 підручника: 696 (2; 4; 6); 700; 702; 704; 706; 709
Завдання 4.
Письмово виконай вправи:
- Із 360 т цукрового буряка отримали 57,6 т цукру. Який відсоток цукру в цукровому буряці?
- Зроблено 50 кидків. 5 дротиків пролетіли мимо цілі. Визначте відсоток попадань.
- В 6-А класі 28 учнів. З математики в першому семестрі 8 учнів отримали «11», 13 учнів – «9». В 6-Б класі 25 учнів. З математики в першому семестрі 3 учні отримали «11», 17 – «9». Який клас навчається з математики краще?
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 5.
Письмово виконай вправи, стор. 136: 719; 721.
Уроки №12, 13
«Не будьмо чванливі, не дражнімо
один одного, не завидуймо один одному!»
Послання апостола Павла до галатів 5:26
Фронтальне опрацювання матеріалу
Відсоткові розрахунки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 4.
- Усно дай відповіді на питання:
- Що називають відношенням чисел?
- Які величини називають прямо пропорційними?
- Пропорція – це…
- Сформулюй основну властивість відношення.
- Як читається основна властивість пропорції?
- Що називають відсотком?
- Як знайти відсоток від числа?
- Як знайти число за його відсотками?
- Що називають відсотковим відношенням чисел?
- Що показує відсоткове відношення чисел?
- Як знайти відсоткове відношення чисел?
Завдання 2.
- Уважно прочитай додаток до блоку, розданий учителем.
- Усно дай відповіді на питання:
- Які є типи задач на відсоткові розрахунки?
- Який загальний спосіб їх розв’язування?
- Назви спосіб розв’язування кожного типу задач на відсоткові розрахунки.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Усно виконай вправи, стор. 138 підручника: 730 (1; 3; 5); 731 (2; 4; 6).
Завдання 4.
Письмово виконай вправи:
- Чорнослив при сушінні втрачає 64% своєї маси. Скільки потрібно взяти свіжого чорносливу, щоб отримати 27 кг сушеного?
- Із 15 зрізаних квітів 9 зів'яли. Скільки відсотків зрізаних квітів зів'яли?
- В басейн налили 1400 м3 води, що становить 35% об'єму всього басейну. Чому дорівнює об'єм всього басейну?
- Фермер зібрав з кожного з 9 га своєї плантації 35 т овочів. Консервний завод купив 12% зібраних фермером овочів. Скільки тонн овочів купив консервний завод у фермера?
- За місяць побудовано 60% дороги. Яка довжина всієї дороги, якщо залишилось побудувати 120 км?
- Для приготування компоту змішали 2,5 кг яблук, 2 кг груш и 0,5 кг вишень. Знайди відсотковий вміст кожного виду фруктів, взятих для приготування компоту.
- Шафа має висоту 1,8 м. Її глибина становить 30% висоти, а ширина 250% глибини. Знайди об'єм шафи.
- Підприємство випустило 50 000 акцій. 30% всіх акцій були розподілені між робітниками підприємства, а решта – продані трьом фірмам «Альфа», «Бета» и «Гамма» – у відношенні 1 : 2 : 4. На скільки більше акцій купила фірма «Гамма», ніж «Альфа»?

Готуємось до індивідуального опрацювання
- Знайдіть відсоток вмісту цукру в розчині, якщо 400 г розчину містить 18г цукру.
- Ціна деякого товару зросла від 64 грн. до 80 грн. На скільки відсотків підвищилась ціна товару?
- При сушінні яблука втрачають 84 % своєї ваги. Скільки треба взяти свіжих яблук, щоб отримати 64 кг сушених?
- У посудині є 20%-й розчин солі. Скільки кілограмів дистильованої води треба додати до 20 кг розчину, щоб концентрація розчину зменшилася до 10%-го?
- Вартість деякого товару дорівнювала 600 грн. Спочатку його ціна підвищилась на 20 %, а потім знизилась на 10 %. Якою стала вартість товару після цих змін? На скільки відсотків змінилась початкова ціна?
Урок №15
«Мій Бог, моя Скеля, Він дав мені перемогу»
Тайсон Фʼюрі англійський
боксер-важковаговик
Внутрішньопредметне узагальнення матеріалу
Відношення і пропорції
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори тези 1.1; 1.3; 2.4; 2.5; 3.7; 3.8; 3.9; 4.11; 5.12; 5.13; 5.14; 5.15 блоку № 4.
- Письмово дай відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Запиши 25 % десятковим дробом.
|
А |
Б |
В |
Г |
|
2,5 |
25,0 |
0,25 |
0,025 |
-
Записано пропорцію
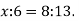 Назви крайні члени пропорції.
Назви крайні члени пропорції.
|
А |
Б |
В |
Г |
|
6 і 8 |
6 і 13 |
х і 8 |
х і 13 |
- Знайди відношення 5 дм : 5 см.
|
А |
Б |
В |
Г |
|
5 |
6 |
10 |
8 |
Завдання 3.
Письмово виконай вправи:
-
Розв’яжи рівняння:
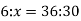 .
.
- Відстань на карті між двома містами дорівнює 24 см. Яка відстань між цими містами на місцевості, якщо масштаб карти 1 : 400 000?
- Периметр трикутника дорівнює 108 см, а довжини сторін відносяться як 6 : 8 : 13. Знайти довжини сторін трикутника.
- До 160 г 15-відсоткового розчину солі долили 40 г води. Знайди у відсотках вміст солі в новому розчині.
- Вартість костюма дорівнювала 160 грн. Спочатку його ціна підвищилась на 20 %, а потім знизилась на 10 %. Якою стала вартість костюма після цих змін? На скільки відсотків змінилась початкова ціна?
Тема №5. Коло і круг
Урок №1

Коло і круг
«Заняття геометрією непомітно
приводить людський розум до винаходів»
Дені Дідро, французький філософ і енциклопедист
Питання
- Коло.
- Круг.
- Діаграми.
Література
Істер О.С. Математика: підручник для 6 класу, Київ: «Генеза», 2014. – §§ 29 – 31, стор. 140 – 153.
|
1. Коло |
||
|
1.1 |
Геометрична фігура, яка складається з усіх точок площини, які знаходяться на однаковій відстані від даної точки, називається колом. |
|
|
1.2 |
Задана точка називається центром кола. |
|
|
1.3 |
Відрізок, який сполучає центр кола з будь-якою його точкою, називається радіусом кола (прийнято позначати буквою r) |
|
|
1.4 |
Відрізок, який сполучає будь-які дві точки кола і проходить через його центр називається діаметром кола (прийнято позначати буквою d). d = 2r |
|
|
1.5 |
Довжина кола прямо пропорційна його діаметру (для всіх кіл відношення довжини кола до його діаметра є одним і тим самим числом): |
|
|
1.6 |
Довжина кола дорівнює добутку числа π на діаметр кола: |
|
|
|
2. Круг |
|
|
2.7 |
Частина площини, яка лежить усередині кола, разом із колом утворюють круг. |
|
|
2.8 |
Центр, радіус, діаметр кола одночасно є центром, радіусом і діаметром круга. |
|
|
2.9 |
Відстань від центра до будь-якої точки круга не перевищує радіуса круга. |
|
|
2.10 |
Площа круга дорівнює добутку числа π на квадрат радіуса: |
|
|
2.11 |
Якщо з центра круга провести два радіуси, то вони поділять круг на дві частини, кожна з яких називається круговим сектором.
|
|
|
2.12 |
Діаметр розбиває круг на два півкруги. Кут півкруга дорівнює 180º. |
|
|
2.13 |
Сума кутів півкругів утворює повний кут. Градусна міра повного кута дорівнює 360º
|
|
|
|
3. Діаграми |
|
|
3.14 |
Діаграма – це один із графічних способів зображення співвідношення між величинами, які порівнюють. |
|
|
3.15. |
Зображення співвідношення між величинами у вигляді прямокутників називається стовпчастою діаграмою. |
|
|
3.16 |
Зображення співвідношення між величинами у вигляді кругових секторів називається круговою діаграмою.
|
|
Уроки №2, 3
«Щоб оволодіти знанням,
потрібно засвоювати їх із задоволенням»
Анатоль Франс, французький письменник
Фронтальне опрацювання матеріалу
Коло. Довжина кола
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1. – 1.6 блоку № 5.
- Дай відповіді на питання:
- Що називається колом?
- Центр кола – це …
-
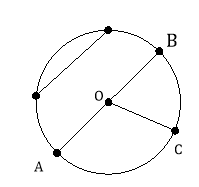 Що називають радіусом кола?
Що називають радіусом кола?
- Що таке діаметр?
- Яку властивість має діаметр кола?
- Як пов’язані довжина кола і його діаметр?
- За якими формулами шукають довжину кола?
-
Чому дорівнює число
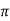 ?
?
Завдання 2.
Назви на малюнку радіуси кола, діаметр кола.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконати роботу у практичному зошиті «Я дослідник», тема 5.
Завдання 4.
Виконати роботу у практичному зошиті «Я дослідник», тема 6.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних вправ
Завдання 5.
Спробуй за допомогою геометричних фігур намалювати тварин, користуючись зразками малюнків за допомогою кіл ось таких тварин (завдання на ІОМ):
Урок №4
«Хто стереже уста свої і язика
свого, той береже від лиха душу свою»
Книга приповістей Соломонових 20:23
Фронтальне опрацювання матеріалу
Круг. Площа круга. Круговий сектор
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.12 блоку №5.
- Дай відповіді на питання:
- відрізок, що з’єднує точку кола з центром це …
- частина площини, обмежена колом разом з цим колом це …
- множина точок, рівновіддалених від однієї точки це …
- Як знайти довжину кола?
- Який зв'язок існує між радіусом і діаметром кола?
- Назви основні елементи круга.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Виконати роботу у практичному зошиті «Я дослідник», тема 7.
Урок №5
«Золоті яблука в срібних прозорих
посудинах – слово, сказане пристойно»
Книга приповістей Соломонових 24:11
Фронтальне опрацювання матеріалу
Стовпчасті та кругові діаграми
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.16 блоку № 5.
- Дай відповіді на питання:
- Що називають колом?
- Що називають кругом?
- Які елементи кола і круга ти знаєш?
- Що таке діаметр?
- Дай означення радіуса кола.
- Як знайти довжину кола?
- Що називають діаграмою?
- Які діаграми називаються стовпчастими, а які круговими?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Виконати роботу у практичному зошиті «Я дослідник», тема 8.

Готуємось до індивідуального опрацювання
- Опитавши групу хлопців про розмір їхнього взуття, склали таблицю.
|
Розмір взуття |
24,5 |
25 |
25,5 |
26 |
|
Кількість хлопчиків |
35 |
30 |
30 |
25 |
Побудуйте відповідну стовпчикову діаграму.
- Кіт наздоганяє мишу, яка втікає по колу, радіусом 5 см. Мишка пробігла 3 кола. Яку відстань вона подолала?
- Піца, діаметр якої дорівнює 30 см, коштує стільки ж як дві піци, діаметр яких 15 см. У якому випадку Славко з’їсть більше піци: коли придбає одну велику чи дві маленьких піци?
Урок №7
«Отак ваше світло нехай світить перед людьми, щоб вони
бачили ваші добрі діла, та прославляли Отця вашого, що на небі»
Євангелія від Матвія 5:16
Внутрішньопредметне узагальнення матеріалу
Коло і круг
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори тези 1.1 – 3.16 блоку № 5.
- Письмово дай відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Письмово виконай вправи:
- Обчисли площу круга і довжину кола з радіусом 5 см.
- Якщо діаметр кола дорівнює 16 см, то скільки дорівнює його радіус?
- Побудуй коло радіусом 3 см і знайди його діаметр.
- Користуючись діаграмою, дай відповіді на запитання:
- Скільки було сонячних днів у місяці?
- Скільки було хмарних днів?
- Скільки було днів, коли йшов дощ?
- Яких днів було найбільше? найменше?
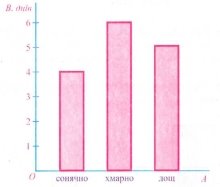
- Накресли довільний трикутник. Проведи три кола так, щоб сторони трикутника були їх діаметрами.
- Радіус першого круга 8 см, другого – 2 см. У скільки разів площа першого круга більша за площу другого круга?
- Піца, діаметр якої дорівнює 50 см, коштує стільки ж скільки дві піци, діаметр яких 25 см. У якому випадку Іринка з’їсть більше піци: коли придбає одну велику чи дві маленьких піци?
Повторення матеріалу, вивченого у І семестрі
Урок №1
«Пізнавай себе, вдосконалюйся,
вчися тому, до чого маєш здібності»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Узагальнення матеріалу, вивченого у І семестрі
І. Усно виконати вправи
-
Обчисли:
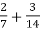 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Обчисли:
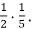
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Дана пропорція
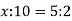 . Назвіть крайні члени пропорції.
. Назвіть крайні члени пропорції.
|
А |
Б |
В |
Г |
|
2 |
5 |
10 і 5 |
|
ІІ. Письмово виконати вправи
- Знайди найбільший спільний дільник чисел 24 і 18.
-
Обчисли:
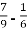 .
.
-
Обчислити:
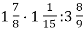 .
.
- Периметр трикутника дорівнює 625см, а довжини сторін відносяться як 4 : 9 : 12. Знайти довжини сторін трикутника.
- Пальто коштувало 80грн. Спочатку воно подорожчало на 10%, а потім подешевшало на 20%. Якою стала ціна пальта після цих змін? На скільки відсотків змінилась початкова ціна?
~ 1 ~


про публікацію авторської розробки
Додати розробку