Позакласний захід "Математика і мистецтво"







Свято «Математика і мистецтво»
«… математика – один з видів мистецтва».
Н. Вінер
1 вед. Математика пронизує все наше життя. Математичні формули та закономірності не лише описують форму та якість матеріальних предметів навколишнього середовища, вони виражають певні події або явища життя.
2. вед. Математика в перекладі з грецької означає «знання , наука». Математика – цариця усіх наук, символ мудрості. Краса математики є однією з ланок, що пов’язує науку і мистецтво.
1 вед. Мабуть, кожен з вас зараз подумав, який же ж зв’язок може бути між математикою та творами мистецтва. Як можуть взаємодіяти такі, зовсім різні, людські культури. Сьогодні, ми пропонуємо вам знайти відповіді, довести, що зв’язок між математикою і мистецтвом існує. Для цього потрібно лише поміркувати, згадати, зрозуміти, послухати, і найголовніше, захотіти кожному відповісти на це питання.
2. вед. А розпочнемо наше свято зі слів відомих людей науки, які неодноразово замислювались над питанням взаємозв’язку математики і мистецтва.
Бе́ртран А́ртур Уи́льям Ра́ссел, британський філософ, і математик писав:
«Математика володіє не тільки істиною, а й найвищою красою – красою відточеною і суворою, … піднесено чистою і такою, що прагне до справжньої досконалості, яка властива тільки найкращим зразкам мистецтва.»
1 вед. Ігорь Іва́нович Сіко́рський — російський і американський авіаконструктор, учений, винахідник, філософ, говорив:
«Математика – не тільки наука, а й мистецтво, і то прекрасне мистецтво. Естетичні почуття є, власне, головним стимулом праці для математика – теоретика.»
2. вед. Виктор Фукс - американский экономист і філософ вважав:
«Не існує методів, оволодівши якими можна було б створювати великі твори в галузі музики, поезії чи образотворчого мистецтва, методів, яких можна було б навчати і якими можна було б навчитися користуватися. Однак є метод, що дає змогу відкривати закономірності в природі; цей метод можна вивчити , ним можна оволодіти. Метод, про який іде мова, - спостереження, експеримент і математичний опис – спорадично застосовувався вже протягом тисячоліть. Та лише завдяки Галілею, Кеплеру і Ньютону він став великим, доступним для всіх шляхом пізнання природи.»
- вед . Отож, як бачимо, зв’язок між математикою і мистецтвом справді існує. Давайте розглянемо окремі види мистецтв і як на них впливає математика.
Сторінка І. Математика і література.
Это ложь, что в науке поэзии нет.
В отраженьях великого мира
Сотни красок и звуков уловит поэт,
И повторит волшебная лира.
За черточками формул, забыв о весне,
В мире чисел бродя, как лунатик,
Вдруг гармонию выводов дарит струне,
К звучной скрипке прильнув, математик.
Настоящий ученый, он тоже поэт,
Вечно жаждущий знать и предвидеть,
Кто сказал, что в науке поэзии нет?
Нужно только понять и увидеть!
2 вед: В уявленні багатьох , математики – це “сухарі”, занурені у свою науку і ні чим іншим не цікавляться.
1 вед: Помилка ця - от знання того, что геніальність сумісна тілько с особистістю захопленою, різностороннє розвинутою , глибокою та змістовною.
2 вед: Великий математичний талант нерідко поєднується с виявленням творчого інтересу до поезії.
1 вед: Нам відомо не мало вчених-математиків, які писали вірші.
Учень 1: Софія Василівна Ковалевська (1850 – 1891
Учень. Омар
Вед. 2. Великий російський учений М.В. Ломоносов свого часу говорив про математику так: «Математику вже для того вчити потрібно, що вона розум до ладу приводить». Крім математики, хімії, фізики та інших наук , Ломоносов ще й займався написанням віршів.
Вед 1. А хіба не писал вірші великий російський геометр Лобачевский? Ректор Казанського университету та відомий математик раптово у 1834 році “ризикнув” надрукувати свій вірш “Разлив Волги при Казани”.
Вед.2. Ця публикація, мабуть, пов’язана з приїздом Пушкіна до Казані у вересні 1833 року, де він збирав матеріали про повстання Пугачова. Дружина Лобачевского – сестра Великопольского, давнього приятеля Пушкіна, на вечорах якого бували Пушкін та Лобачевский. Зустрілися два генія. Може бути, що саме після зустрічі з Лобачевским Пушкін написав: “Натхнення потрібне в поезії, як в геометрії”.
Вед.1. Як бачимо , вченим не чужа поезія
То́мас Хілл Грін, английский философ говорив:
«Математику звичайно розглядають, як щось цілком протилежне до поезії. А проте Математика і Поезія – якнайспорідненіші, оскільки вони обидві – вивір уяви. Поезія – це творення, побудова, вигадка; так само й математику певні її прихильники називали найвеличнішою і найчарівнішою вигадкою. Бо й справді вона не тільки наука , а й мистецтво.»
Вед 2. А тому натхнення у математиці знаходили і поети.
Одним з прикладів такого використання математичних закономірностей є видатна трагедія Гете «Фауст».
Учень. У цьому творі
Вед.2 .Не тільки Льюіс Керрол, а багато з видатних математиків були одночасно і письменниками. Наприклад, відомого французького математика Рене Декарта (1596 – 1650вважають одним із засновників мови французької прози. Розпочавши із «закоханості в поезію», він залишився відданим їй, і останнім його творінням була п’єса у віршах, яка була написана у Стокгольмі.
.
Вед. 1. Видатні математики – це люди високої ерудиції. Наш славетний співвітчизник, вчений, математик Михайло Васильович Остроградський (1801 – 1862) був людиною високого рівня духовної культури, досконало володів французькою мовою, був добре обізнаний з французькою літературою, не кажучи вже про російську. Але українська мова, мова його батьків, його народу була для нього найдорожчою. І хоча він міг годинами читати монологи з Мольєра та Корнелія, улюбленим його поетом був Тарас Шевченко, значну частину віршів якого він знав напам’ять . Як згадував Т.Шевченко, Остроградський приймав його у себе вдома, як рідного.
Вед. 2 Не можна не згадати і найславетнішого математика в історії людства Леонарда Ейлера (1707 – 1783). За все своє життя Ейлер написав 886 робіт з різних галузей науки. А ще він добре знав кращих письменників давнини, стародавню літературу з математики, історію всіх часів і народів, володів багатьма мовами стародавнього світу і сучасної Європи, розповідають, що він знав напам’ять «Енеїду» від початку і до кінця.
Вед. 1. Не забувають про математику і сучасні письменники. Давайте послухаємо уривок з твору Анатолія Дімарова «На коні і під конем»
- Учень:
Вед. 2. І таких уривків з художніх творів існує безліч. А зараз переходимо до наступного нашого розділу:
Математика та живопис.
Вед.1. Людина розрізняє предмети, які її оточують за формою. Інтерес до форми будь - якого предмету може бути викликаний красою форми. А форма, в основі якої лежить поєднання симетрії та золотого перерізу, допомагає найкращому її зоровому сприйманню і появі відчуття краси та гармонії.
 Учень. Ще у епоху …
Учень. Ще у епоху …
Вед. 2. Історик і мистецтвознавець Олексій Карпович Дживелегов писав:
«Живопис приходив до математики через учіння про перспективу і через оптику , скульптура – через учіння про пропорції , архітектура – через учення про масу й вагу тіл і через те ж учіння пропорції. Мистецтво ставало наукою. Ніхто не почував цього так ясно і сильно, як Леонардо да Вінчі, і недарма в його творчості мистецтво й наука стали двома сторонами одного й того самого, чимось неподільним.»
Учень: учений Леонардо да Вінчі
Учень: А зараз до вашої уваги картина І.І. Шишкіна «Сосновая роща»
Учень:
Працюючи над картиною «Бояриня Морозова
Вед.1
А зараз давайте ближче познайомимося із Альбрехтом Дюрером (1471 – 1528). Живописець, гравер, гуманіст, учений, Дюрер був першим художником у Німеччині, який вивчав математику і механіку, будівельну і фортифікаційну справи. Він перший у Німеччині намагався застосувати в мистецтві свої наукові знання в галузі перспективи і пропорцій.
Ось найзнаменитіша гравюра художника «Меланхолія»
А.Дюрер «Меланхолія»
На цій гравюрі Меланхолія оточена атрибутами геометрії та архітектури, і , мабуть думка про безмірність знання повергає її у бездіяльність і відчай. На гравюрі розв’язана складна геометрична задача побудови перспективи додекаедра, а у правому верхньому кутку зображений магічний квадрат, складений з перших чисел натурального ряду, сума яких у будь якій стрічці, стовпці або діагоналі є стала (34).
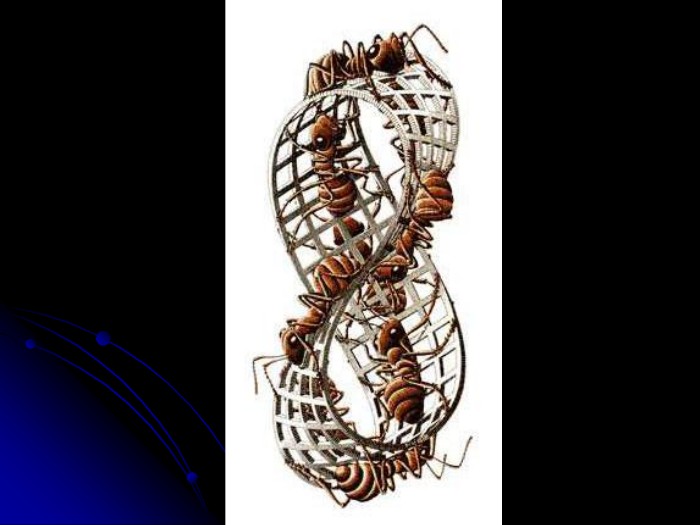
Математика має справу з абстракціями, які створюються у нашій свідомості. І говорячи сьогодні про зв’язок математики та живопису, не можна не згадати про гравюри відомого голландського художника Моріса Корнеліуса Ешера (1898 – 1972). На своїх гравюрах художник показав, як люди можуть давати неправильне тлумачення інформації, яка надходить до органів чуттів, коли оцінюють розміри тіл, інтервали часу, положення предметів у просторі, їх колір. Саме ці особливості сприймання нами тривимірного простору з дивовижною майстерністю використав художник.
Вед.2
Побачити, як математика пов’язана з мистецтвом, можна на прикладі архітектури.
(Слайд «Математика і архітектура»)
Йдучи вулицями міста, можна спостерігати, як геометричні форми використовуються в архітектурі. Подивимось на найвідоміші архітектурні пам’ятки світу: … (слайди)
Ми бачимо колони, арки, ніші, фризи, ажурні бароківські ліплення складної форми. Лише досконале знання архітектором математики дає можливість поєднати здавалося б прості геометричні форми (куб, паралелепіпед, циліндр, еліпс, коло) у складну музику вишуканих будівель.
Результат роботи архітектора повинен бути точним. Його перспективний малюнок повинен відповідати правилам геометрії, зокрема нарисної. Отже , ні один архітектор не обійдеться без знання масштабу, пропорції, симетрії.
Саме симетрія – це врівноваженість, упорядкованість, краса, довершеність, доцільність. Будь-яка архітектурна споруда використовує симетрію. Симетрія використовується в будівництві, техніці і в повсякденному житті.
Вед.1
Остання наша сторінка «Математика і музика»
(слайди…)
Мабуть, кожен з вас зараз подумав, який же ж зв’язок може бути між математикою - мудрою царицею всіх наук, та музикою? Як можуть взаємодіяти, такі, зовсім різні , людські культури? Сьогодні, я пропоную вам знайти відповіді на ці запитання, довести, що зв’язок між музикою і математикою існує.
Вед.2
Музика - найбільш суб'єктивна з наук, і найбільш абстрактно логічна з мистецтв.Бо музика - то є Гармонія Душі.
Людство винайшло дві універсальні гармонічні дисципліни-абстракції, одна з яких опікується логікою й чіткістю сталих законів, а друга - емоційним змістом і життям без кордонів. Перша - математика, друга - музика.
Вед.1
Англійський математик Джеймс Сільвестр говорив:
«Чи не може музика бути описаною як математика почуттів, а математика як музика розуму ? Так, наприклад, музикант відчуває музику, математик розуміє музику, - музика це мрія, математика - ділове життя – кожна повинна дістати своє завершення від другої, коли людський розум, піднесений до досконалого зразка, сяятиме далі, уславлений у якомусь майбутньому Моцар том–Діріхле чи Бетховеном–Гауссом – такий союз виразно виявляється в генії і працях Гельмгольца!»
Учень: Про Піфагора
Вед.2 День відкриття цього факту можна назвати день народження математичної фізики.
А. Енштейн писав: “Ми відкрили щось подібне на коливання струни і атому, що випромінює промені, така система частин веде себе подібно до малого акустичного інструменту, в якому виробляють стоячі хвилі”.
Вед.1
А у листі Х.Гольдбаху у 1712 році великий німецький математик Г.Лейбніц писав: «…Ми в музиці не рахуємо далі п’яти, подібно до народів, які в арифметиці не пішли далі трьох… Всі наші інтервали – це відношення, складені з відношень між двома числами 1, 2, 3, 5… Музика – це прихована математична вправа душі, яка не вміє рахувати…»
Вед.2
Німецький природознавець Г.Гельмгольц говорив:
« У мене завжди викликав жвавий інтерес той дивний факт, що в ученні про звук – у фізичній і технічній основі музики, яка за допомогою короткочасної швидкоплинної дії викликає в нашій душі такі незрозумілі настрої, що не піддаються описові, - виявилась такою корисною математика – наука найстрогішого і чистого мислення.
Вед.1 Майже всі справжні композитори та музиканти розуміли, що в основі музики лежить математика.
Музика не може існувати без нот. Ноти – азбука музиканта. Кожна нота має свою тривалість. Є ноти цілі, половині, четвертні, восьмі, шістнадцяті.
Доведено, що діти, які займаються музикою легше засвоюють
математику. У них добре розвинуті просторова і творча уяви, інтуїція.
Учень.
Математично тривалість нот
Вед.1
Далеко не всі композитори мали абсолютний слух. А , наприклад, Людвігу Ван Бетховену не було ще й тридцяти років, коли він відчув перші ознаки глухоти, яка згодом відокремила його від навколишнього світу і, навіть , наштовхнула його на думку про самогубство. Врятували його від трагічної смерті любов до музики, любов до життя, впевненість у тому, що перемагає той, хто бореться. І уявіть собі, як не знаючи математичних закономірностей побудови музики, можна було б створити такі шедеври як«Місячна соната» або один з найвідоміших творів Бетховена – симфонія № 5.
Вед.2 Великий композитор Вольфганг Амадей Моцарт, пишучи свої вальси і менуети, використовував заснований на теорії ймовірностей «механічний пристрій» - кубик. Про нього А.Моль писав: «Винайдений Моцартом спосіб компонувати мелодію за допомогою гри в кості над спеціальною таблицею, яка визначає вибір наступного такту створюваної п’єси, свідчить про те, що великі композитори чітко усвідомлювали роль випадковості в загальній побудові музичного повідомлення», тобто роль теорії ймовірностей – Одного з розділів математики.
Вед.1
Зараз математики почали розглядати музичну партитуру як графік, на якому по вертикалі відкладається висота звуку, а по горизонталі – час. Інші характеристики – тональність, тривалість звучання, паузи, ритм тощо – додаються, але за допомогою додаткових символів . Тепер у нас є докази того, що кожний акорд можна представити не просто за допомогою довільних знаків на розлінованому папері, але і як точку в геометричному просторі.
Вед.2 Ще раз згадаємо про славетного математика Леонарда Ейлера. Він полюбляв слухати музику, яка дещо відволікала його від напруженої праці і навіть писав трактат про нову теорію музики, про який говорили, що в ньому багато музики для математиків і водночас надто багато математики для музикантів.
Вед.1
Професор Київського Державного університету ім. Т.Г. Шевченка Микола Іванович Кованцов писав:«Ейлер у математиці – це Моцарт у музиці, Пушкін у поезії, Мікеланджело в живопису»
Вед.2 Ми , звичайно, моли б знайти ще багато прикладів взаємодії математики та мистецтва. Тепер кожен з вас може впевнено про це заявити та відстояти свою точку зору.
І на завершення давайте послухаємо уривок з одного з творів В.А.Моцарта, це прекрасний вальс «Вальс Квітів» (звучить музика…)
1
Софія Василівна Ковалевська (1850 – 1891). Маловідомим є той факт, що ця видатна жінка – математик, народжена Круковська, має українське коріння: її батьки з Полтавщини, родичі Косачів (Лесі Українки). Освіту здобула домашню. Але її навчали гарні педагоги. Математичні здібності виявилися вперше у віці 13 років. Для здобуття вищої освіти Ковалевська у 18 років виїхала за кордон до Берліна. Одним з її учителів був видатний математик К. Вейєрштрасс, який пізніше казав, що в нього не було учнів, які б могли б зрівнятися здібностями , старанністю й любов’ю до науки з Ковалевською. Ще свого часу відомий учений Сергій Вавілов писав про неї: «В історії людства до Ковалевської не було жінок, рівних їй за силою і спорідненістю математичного таланту». Найбільш важливі дослідження вченої відносяться до теорії обертання твердого тіла. Вона працювала також у галузі теорії потенціалу , математичної фізики, небесної механіки.
У 24 роки з докторським дипломом в кишені Ковалевські повертається з-за кордону до Петербурга, але, на жаль, не може застосовувати свої знання – для жінок наукова кар’єра в Росії була закритою. У цей час вона розпочинає свою літературно – публіцистичну діяльність. Серед її знайомих не лише вчені – Д. Менделєєв, П. Чебишев, але й письменники – Ф. Достоєвський, І . Тургенєв. До речі, Достоєвський сприяв пробудженню літературного таланту Ковалевської. Вона володіла п’ятьма мовами, писала статті в газети, театральні рецензії , оповідання, романи , вірші.
Послухайте один з її віршів
“ЕСЛИ ТЫ В ЖИЗНИ…”
Если ты в жизни, хотя на мгновенье
Истину в сердце своем ощутил,
Если луч правды сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Чтобы в решеньи своем неизменном
Рок ни назначил тебе впереди –
Память об этом мгновеньи священном
Вечно храни, как святыню, в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной
Бурю ты встреть и померься с грозой.
Учень. Омар Хайям – видатна особистість Сходу ХІ століття. Вже 9 століть ім’я Хайяма знайоме людству. Математик, філософ, астроном, перекладач, поет. Особистість незвичайна. Навіть вважали, що це дві різні людини. У 42-му томі енциклопедії Блокгауза і Ефрона можна прочитати: Омар Хайям – математик, астроном ХІ ст., а в 73-му: Хайям – перський поет. У чому справа? У тому, що математичні праці Хайяма дійшли до Європи у 1851 р., вірші ж перекладено англійською у 1859 р. поетом Фіцжеральдом. І спочатку ніхто не здогадувався, що вірші й математичні праці належать одній і тій самій людині. Не дивно, що цю помилку повторила енциклопедія у ХІХ ст..
Але справа не в енциклопедії. Мабуть люди вирішили, що мистецтво та наука - явища дуже різні, щоб ними займалася одна людина. Але вчений та художник в одній особі – це не суперечність, а, навпаки, гармонія. Коротенькі вірші Хайяма – рубаї – поєднання математичної точності та сердечного трепету.
Рубаи Омара Хайяма:
О тайнах сокровенных невеждам не кричи,
И бисер знаний ценных перед глупым не мечи,
Будь скуп в речах и прежде взгляни, с кем говоришь,
Лелей свои надежды, но прячь от них ключи.
То, что судьба тебе решила дать,
Нельзя ни увеличить, ни отнять.
Заботься не о том, чем не владеешь,
А от того, что есть, свободным стать.
Учень. У цьому творі описано ситуацію, де відьма готує омолоджуюче зілля й одночасно читає закляття. Слова, що промовляє відьма, видаються повним абсурдом:
З одиниці робиш десять,
Пропускаєш два,
А також три.
Закреслюєш чотири.
З п’ять і шість
Робиш сім і вісім (і навпаки).
Квадрат готовий.
Відповідно до поданих рекомендацій будуємо «магічний квадрат» - символ нового життя Фауста. Складаємо його з перших 9-ти натуральних чисел.
|
1 |
2 |
3 |
|
4 |
5 |
6 |
|
7 |
8 |
9 |
Тоді:
- З 1 робимо 10 (1 замінюємо на 10);
- Пропускаємо числа 2 і 3;
- Закреслюємо 4 – замінюємо 0;
- Замінюємо 5 і 6 відповідно на 7 і 8, а 7 і 8 - на 5 і 6;
- В останній клітинці вписуємо 4 (про це відьма не каже, ніби ховаючи справжнє закляття)
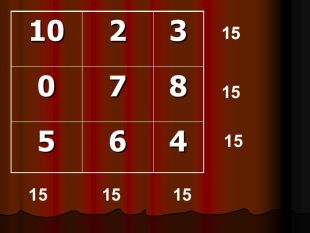
|
10 |
2 |
3 |
|
0 |
7 |
8 |
|
5 |
6 |
4 |
Як бачимо, даний квадрат «напівмагічний», оскільки сума чисел є сталою (рівною 15) за стовпцями і рядками, але не за діагоналями.
Уривок з твору Анатолія Дімарова «На коні і під конем»
Учень: «…Він уже мав колись мороку з отакою задачкою. Там розповідалося, що один господар мав три барани і чотири кози. «То скільки ж всього було голів ?» - запитувалося під кінець.
Ванько, що саме стояв біля дошки, недовго міркував. Взяв шмат крейди, звівся навшпиньки і вивів на дошці : 3 барани додати 4 кози – буде одна голова.
- Як одна? - здивувалась вчителька. – Ану порахуй: три додати чотири, то скільки буде ?
Наморщивши лоба, Ванько почав рахувати на пальцях.
- Буде сім.
- От бачиш !.. То скільки буде всього голів, коли до трьох баранів додати чотирьох кіз ?
- Один голова!
Як не билася з ним вчителька, так вона і не змогла втовкмачити , що худобу можна рахувати на голови. Ванько знав лише одного голову – сільради і не хотів поступатися цим, хоч у ступі товчи.
Повертаючись зі мною додому, він все бубонів:
- Хіба ж у баранів голови бувають ? .. То тільки в нашому селі голова – дядько Никифор.. І який дурень триматиме у себе аж три барани та ще до них чотири кози додаватиме? – хазяйнувато запитував він. – Двох баранів і чотирьох кіз треба продати, а натомість купити овець. Отоді вже їх зводити до купи…»
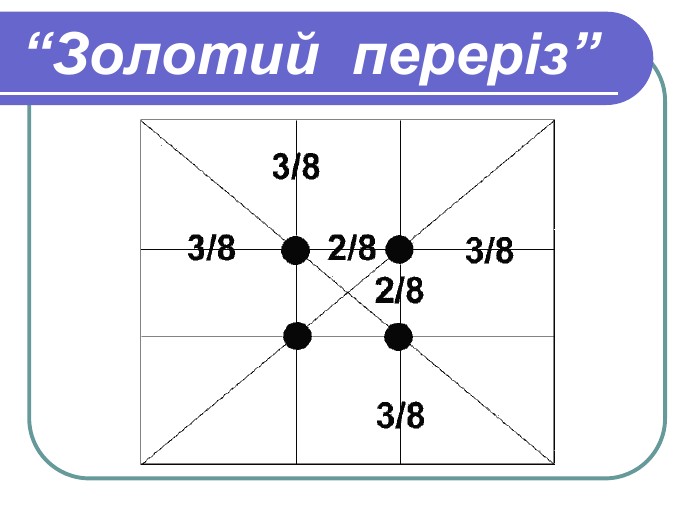
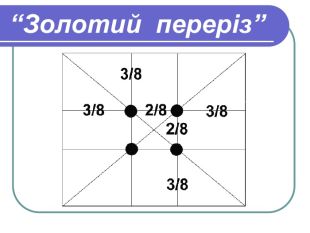
 Учень. Ще у епоху Відродження художники відкрили, що будь- яка картина має певні точки, що мимоволі привертають нашу увагу, так звані зорові центри. Таких точок всього чотири, і розміщені вони на відстані 3/8 та 5/8 від відповідних країв площини.
Учень. Ще у епоху Відродження художники відкрили, що будь- яка картина має певні точки, що мимоволі привертають нашу увагу, так звані зорові центри. Таких точок всього чотири, і розміщені вони на відстані 3/8 та 5/8 від відповідних країв площини.
Це відкриття у художників того часу отримало назву «золотий переріз» картини. Золотий переріз – гармонійна пропорція.
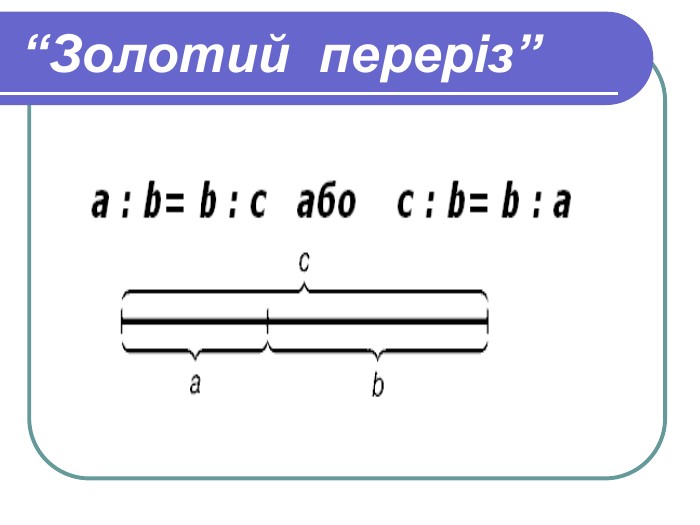
Це такий пропорційний поділ відрізка на нерівні частини, при якому довжина усього відрізка відноситься до більшої частини, як сама більша частина відноситься до меншої:
|
a : b= b : c або с : b= b : а |
|
|
|
|
Пропорція золотого перерізу - це приблизно 8:5, а ще точніше - 13:8. Художник Альбрехт Дюрер встановив, що зріст людини ділиться в золотих пропорціях лінією поясу.Талія ділить ідеальне людське тіло відносно золотого перетину. Пропорції чоловічого тіла коливаються в межах середнього відношення 13:8 і трохи ближче підходять до золотого перерізу, ніж пропорції тіла жінок (8:5), які змушені "урівнювати" фігуру за рахунок підборів.
Учень:
Саме вивченню «золотого перерізу» приділяв багато своєї уваги великий італійський художник, учений Леонардо да Вінчі .Особистість Леонардо да Вінчі – одна із загадок у історії. Сам учений говорив: «Нехай ніхто, не будучи математиком, не наважиться читати мої праці». Він дістав славу талановитішого художника, великого ученого, генія, що передбачив багато винаходів, які не були впроваджені майже до ХХ ст.
Його картина «Таємна вечеря» демонструє нам використання гармонійної пропорції «золотого перерізу».
Портрет Мони Лізи (Джоконди) багато вже років притягує увагу дослідників, які виявили, що композиція малюнку базується на золотих трикутниках, що є частинами правильного зірчастого п’ятикутника.
Існує дуже багато версій про історію цього портрету. Ось одна з них.
«Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.
Сказка
Жил-был один бедный человек, было у него четыре сына: три умных, а один из них и так, и сяк. И вот пришла за отцом смерть. Перед тем, как расстаться с жизнью, он позвал к себе детей и сказал: “Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастья. Пусть каждый из вас чему-нибудь научится, чтобы мог кормить сам себя”. Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи. Пришел первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел ее: как искусный мастер он сшил для нее красивую шелковую одежду. Третий сын украсил женщину золотом и драгоценными камнями – ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и еще умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: “Ты должна быть моей женой”. Но женщина ответила: “Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями.
А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь”.
Кончив сказку, Леонардо взглянул на Монну Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано – художник пробудил равнодушную статую; улыбка блаженства, медленно исчезая с ее лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно ее храня, не может сдержать торжество. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель...»
Учень: А зараз до вашої уваги картина І.І. Шишкіна «Сосновая роща»
|
На цій відомій картині з очевидністю проглядаються мотиви золотого перерізу. Яскраво освітлена сонцем сосна (що стоїть на першому плані) ділить довжину картини за золотим перерізом. Праворуч від сосни – освітлений сонцем пагорб. Він ділить за золотим перерізом праву частину картини по горизонталі. Ліворуч від головної сосни знаходиться безліч сосен - при бажанні можна з успіхом продовжити поділ картини за золотим перерізом и далі. |
|
|
|
|
Учень:
Працюючи над картиною «Бояриня Морозова», російський художник Василь Суриков мав викликати у глядача ілюзію руху саней, в яких везуть розкольницю. Чуття підказувало, що сани «поїдуть», тільки коли полоззя помістити на строго визначеній відстані від рами. І художник шукав її, пробуючи різні варіанти. Він записав тоді: «У русі є живі точки, а є мертві. Це справжня математика. Фігури, що сидять на санях, тримають їх на місці. Треба було знайти відстань від рами до саней, щоб пустити їх у хід. Трохи менша відстань, - сани стоять.» Саме пропорції «золотого перерізу» пояснюють таємницю емоційного впливу картини «Бояриня Морозова» на глядача, таємницю «чарівної сили» живопису
Учень:
Ідея про можливість побудови числової моделі світу була покладена Піфагором в основу його теорії музики. Про Піфагора відома така історія
«Однажды, размышляя над проблемой гармонии, Пифагор проходил мимо мастерской медника, который склонился над наковальней с куском металла. Заметив различие в тонах между звуками, издаваемыми различными молоточками и другими инструментами при ударе о металл, и тщательно оценив гармонии и дисгармонии, получающиеся от комбинации этих звуков, Пифагор получил первый ключ к понятию музыкального интервала. Он вошел в мастерскую и после тщательного осмотра инструментов и прикидывания в уме их вес вернулся в собственный дом, сконструировал балку, которая была прикреплена к стене, и приделал к ней через равные интервалы четыре струны, во всем одинаковые. К первой из них прикрепил вес в двенадцать фунтов, ко второй - в девять, к третьей - в восемь, и к четвертой - в шесть фунтов. Эти различные грузы соответствовали весу молотков медника. Пифагор обнаружил, что первая и четвертая струны, когда звучат вместе, дают гармонический интервал октавы, потому что удваивание веса имело тот же эффект, что и укорачивание струны наполовину. Натяжение первой струны было в два раза больше, чем четвертой струны, и, как говорят, их соотношение равно 2:1, или двукратное. Подобным же рассуждением он пришел к заключению, что первая и третья струны дают гармонию квинту. Натяжение первой струны было в полтора раза больше, нежели третьей струны, и их соотношение было 3:2, или полуторное.»
Одже, Піфагор винайшов, що якісні відміни в звучанні струн обумовлюються чисто кількісними відмінностями, а саме натягом струн. Одночасне звучання двох струн буде приємне для слуху якщо їх натяги відноситься, як 1:2, або 2:3, або 3:4, що відповідають музичним інтервалом в октаву, квінту і кварту.
Учень.
Математично тривалість нот записують за допомогою звичайних
дробів. Ціла – 1, половина -1/2, четвертна -1/4, восьма – 1/8, шістнадцята – 1/16.
|
математика |
Музика ( тривалість нот) |
|
Ціле число (торт) |
Ціла нота |
|
Ділимо пополам (половина торта) |
Половина цілої ноти - половинна |
|
Ділимо торт на чотири частини (отримуємо одну четверту) |
Ділимо цілу ноту на 4 частини – ( четвертна) |
|
На вісім ( одна восьма) |
На вісім ( восьма , восьмушка) |
|
На шістнадцать ( одна шістнадцята) |
На шістнадцять ( Шістнадцята) |
Отже, ми бачимо, ноти позначаються з допомогою знаків, а їх тривалість визначається математичним рахунком.
А чи існують у музиці математичні дії? « Музичне множення»
записують так: після знака ноти ставлять крапку, це означає, що тривалість ноти
потрібно збільшити в півтора рази.
♪♪ - цей запис є «музичне додавання»- збільшення тривалості двох однакових за висотою нот.
Пропонуємо вам виконати музичні сувеніри-приклади, де числа
зашифровані тривалістю нот.
Учень. Справжнє ім’я його – Чарльз Лютвидж Доджсон (1832 – 1898). Він був професором математики Оксфордського університету, працював у галузі математичної логіки. Його книжки про пригоди Аліси – улюблені твори маленьких і дорослих у багатьох країнах, а для математиків невичерпне джерело різних цитат та епіграфів. Коли англійська королева Вікторія вперше прочитала книгу про Алісу, вона була в такому захопленні, що наказала негайно скупити і привезти їй все, що написав автор цієї книжки, її наказ було виконано з точністю – наступного дня перед королевою лежала купа наукових праць з математики.
Але найбільше Льюіс Керрол любив придумувати і розплутувати загадки. Візьміть хоча б таку:
Господар мав у вітальні тільки одне вікно – квадратне вікно висотою у три фути. Вікно пропускало так багато світла, що в чоловіка почали боліти очі. Тоді він викликав майстра і попросив переробити вікно так, щоб потік світла зменшився вдвічі, тобто площа вікна повинна бути вдвічі меншою. Але вікно, як і раніше, мало залишатись квадратним – в три фути висотою і в три фути шириною. Використовувати занавіски, жалюзі, кольорове скло і подібні хитрощі заборонялось. Як вдалось виконати це замовлення?
(Відповідь: Квадрат нового вікна мав вершини в серединах сторін старого)
Позакласний захід «Математика і мистецтво»
«… математика – один з видів мистецтва».
Н. Вінер
1 вед. Математика пронизує все наше життя. Математичні формули та закономірності не лише описують форму та якість матеріальних предметів навколишнього середовища, вони виражають певні події або явища життя.
2. вед. Математика в перекладі з грецької означає «знання , наука». Математика – цариця усіх наук, символ мудрості. Краса математики є однією з ланок, що пов’язує науку і мистецтво.
1 вед. Мабуть, кожен з вас зараз подумав, який же ж зв’язок може бути між математикою та творами мистецтва. Як можуть взаємодіяти такі, зовсім різні, людські культури. Сьогодні, ми пропонуємо вам знайти відповіді, довести, що зв’язок між математикою і мистецтвом існує. Для цього потрібно лише поміркувати, згадати, зрозуміти, послухати, і найголовніше, захотіти кожному відповісти на це питання.
2. вед. А розпочнемо наше свято зі слів відомих людей науки, які неодноразово замислювались над питанням взаємозв’язку математики і мистецтва.
Бе́ртран А́ртур Уи́льям Ра́ссел, британський філософ, і математик писав:
«Математика володіє не тільки істиною, а й найвищою красою – красою відточеною і суворою, … піднесено чистою і такою, що прагне до справжньої досконалості, яка властива тільки найкращим зразкам мистецтва.»
1 вед. Ігорь Іва́нович Сіко́рський — російський і американський авіаконструктор, учений, винахідник, філософ, говорив:
«Математика – не тільки наука, а й мистецтво, і то прекрасне мистецтво. Естетичні почуття є, власне, головним стимулом праці для математика – теоретика.»
2. вед. Виктор Фукс - американский экономист і філософ вважав:
«Не існує методів, оволодівши якими можна було б створювати великі твори в галузі музики, поезії чи образотворчого мистецтва, методів, яких можна було б навчати і якими можна було б навчитися користуватися. Однак є метод, що дає змогу відкривати закономірності в природі; цей метод можна вивчити , ним можна оволодіти. Метод, про який іде мова, - спостереження, експеримент і математичний опис – спорадично застосовувався вже протягом тисячоліть. Та лише завдяки Галілею, Кеплеру і Ньютону він став великим, доступним для всіх шляхом пізнання природи.»
- вед . Отож, як бачимо, зв’язок між математикою і мистецтвом справді існує. Давайте розглянемо окремі види мистецтв і як на них впливає математика.
Сторінка І. Математика і література.
Это ложь, что в науке поэзии нет.
В отраженьях великого мира
Сотни красок и звуков уловит поэт,
И повторит волшебная лира.
За черточками формул, забыв о весне,
В мире чисел бродя, как лунатик,
Вдруг гармонию выводов дарит струне,
К звучной скрипке прильнув, математик.
Настоящий ученый, он тоже поэт,
Вечно жаждущий знать и предвидеть,
Кто сказал, что в науке поэзии нет?
Нужно только понять и увидеть!
2 вед: В уявленні багатьох , математики – це “сухарі”, занурені у свою науку і ні чим іншим не цікавляться.
1 вед: Помилка ця - от знання того, что геніальність сумісна тілько с особистістю захопленою, різностороннє розвинутою , глибокою та змістовною.
2 вед: Великий математичний талант нерідко поєднується с виявленням творчого інтересу до поезії.
1 вед: Нам відомо не мало вчених-математиків, які писали вірші.
Учень 1: Софія Василівна Ковалевська (1850 – 1891). Маловідомим є той факт, що ця видатна жінка – математик, народжена Круковська, має українське коріння: її батьки з Полтавщини, родичі Косачів (Лесі Українки). Освіту здобула домашню. Але її навчали гарні педагоги. Математичні здібності виявилися вперше у віці 13 років. Для здобуття вищої освіти Ковалевська у 18 років виїхала за кордон до Берліна. Одним з її учителів був видатний математик К. Вейєрштрасс, який пізніше казав, що в нього не було учнів, які б могли б зрівнятися здібностями , старанністю й любов’ю до науки з Ковалевською. Ще свого часу відомий учений Сергій Вавілов писав про неї: «В історії людства до Ковалевської не було жінок, рівних їй за силою і спорідненістю математичного таланту». Найбільш важливі дослідження вченої відносяться до теорії обертання твердого тіла. Вона працювала також у галузі теорії потенціалу , математичної фізики, небесної механіки.
У 24 роки з докторським дипломом в кишені Ковалевські повертається з-за кордону до Петербурга, але, на жаль, не може застосовувати свої знання – для жінок наукова кар’єра в Росії була закритою. У цей час вона розпочинає свою літературно – публіцистичну діяльність. Серед її знайомих не лише вчені – Д. Менделєєв, П. Чебишев, але й письменники – Ф. Достоєвський, І . Тургенєв. До речі, Достоєвський сприяв пробудженню літературного таланту Ковалевської. Вона володіла п’ятьма мовами, писала статті в газети, театральні рецензії , оповідання, романи , вірші.
Послухайте один з її віршів
“ЕСЛИ ТЫ В ЖИЗНИ…”
Если ты в жизни, хотя на мгновенье
Истину в сердце своем ощутил,
Если луч правды сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Чтобы в решеньи своем неизменном
Рок ни назначил тебе впереди –
Память об этом мгновеньи священном
Вечно храни, как святыню, в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной
Бурю ты встреть и померься с грозой.
Учень. Омар Хайям – видатна особистість Сходу ХІ століття. Вже 9 століть ім’я Хайяма знайоме людству. Математик, філософ, астроном, перекладач, поет. Особистість незвичайна. Навіть вважали, що це дві різні людини. У 42-му томі енциклопедії Блокгауза і Ефрона можна прочитати: Омар Хайям – математик, астроном ХІ ст., а в 73-му: Хайям – перський поет. У чому справа? У тому, що математичні праці Хайяма дійшли до Європи у 1851 р., вірші ж перекладено англійською у 1859 р. поетом Фіцжеральдом. І спочатку ніхто не здогадувався, що вірші й математичні праці належать одній і тій самій людині. Не дивно, що цю помилку повторила енциклопедія у ХІХ ст..
Але справа не в енциклопедії. Мабуть люди вирішили, що мистецтво та наука - явища дуже різні, щоб ними займалася одна людина. Але вчений та художник в одній особі – це не суперечність, а, навпаки, гармонія. Коротенькі вірші Хайяма – рубаї – поєднання математичної точності та сердечного трепету.
Рубаи Омара Хайяма:
О тайнах сокровенных невеждам не кричи,
И бисер знаний ценных перед глупым не мечи,
Будь скуп в речах и прежде взгляни, с кем говоришь,
Лелей свои надежды, но прячь от них ключи.
То, что судьба тебе решила дать,
Нельзя ни увеличить, ни отнять.
Заботься не о том, чем не владеешь,
А от того, что есть, свободным стать.
Вед. 2. Великий російський учений М.В. Ломоносов свого часу говорив про математику так: «Математику вже для того вчити потрібно, що вона розум до ладу приводить». Крім математики, хімії, фізики та інших наук , Ломоносов ще й займався написанням віршів.
Вед 1. А хіба не писал вірші великий російський геометр Лобачевский? Ректор Казанського университету та відомий математик раптово у 1834 році “ризикнув” надрукувати свій вірш “Разлив Волги при Казани”.
Вед.2. Ця публикація, мабуть, пов’язана з приїздом Пушкіна до Казані у вересні 1833 року, де він збирав матеріали про повстання Пугачова. Дружина Лобачевского – сестра Великопольского, давнього приятеля Пушкіна, на вечорах якого бували Пушкін та Лобачевский. Зустрілися два генія. Може бути, що саме після зустрічі з Лобачевским Пушкін написав: “Натхнення потрібне в поезії, як в геометрії”.
Вед.1. Як бачимо , вченим не чужа поезія
То́мас Хілл Грін, английский философ говорив:
«Математику звичайно розглядають, як щось цілком протилежне до поезії. А проте Математика і Поезія – якнайспорідненіші, оскільки вони обидві – вивір уяви. Поезія – це творення, побудова, вигадка; так само й математику певні її прихильники називали найвеличнішою і найчарівнішою вигадкою. Бо й справді вона не тільки наука , а й мистецтво.»
Вед 2. А тому натхнення у математиці знаходили і поети.
Одним з прикладів такого використання математичних закономірностей є видатна трагедія Гете «Фауст».
Учень. У цьому творі описано ситуацію, де відьма готує омолоджуюче зілля й одночасно читає закляття. Слова, що промовляє відьма, видаються повним абсурдом:
З одиниці робиш десять,
Пропускаєш два,
А також три.
Закреслюєш чотири.
З п’ять і шість
Робиш сім і вісім (і навпаки).
Квадрат готовий.
Відповідно до поданих рекомендацій будуємо «магічний квадрат» - символ нового життя Фауста. Складаємо його з перших 9-ти натуральних чисел.
|
1 |
2 |
3 |
|
4 |
5 |
6 |
|
7 |
8 |
9 |
Тоді:
- З 1 робимо 10 (1 замінюємо на 10);
- Пропускаємо числа 2 і 3;
- Закреслюємо 4 – замінюємо 0;
- Замінюємо 5 і 6 відповідно на 7 і 8, а 7 і 8 - на 5 і 6;
- В останній клітинці вписуємо 4 (про це відьма не каже, ніби ховаючи справжнє закляття)
|
10 |
2 |
3 |
|
0 |
7 |
8 |
|
5 |
6 |
4 |
Як бачимо, даний квадрат «напівмагічний», оскільки сума чисел є сталою (рівною 15) за стовпцями і рядками, але не за діагоналями.
Вед 1. А зараз згадаємо автора всесвітньо відомих книжок «Аліса у країні чудес» та «Аліса у Задзеркаллі» - видатного англійського письменника Льюіса Керрола.
Учень. Справжнє ім’я його – Чарльз Лютвидж Доджсон (1832 – 1898). Він був професором математики Оксфордського університету, працював у галузі математичної логіки. Його книжки про пригоди Аліси – улюблені твори маленьких і дорослих у багатьох країнах, а для математиків невичерпне джерело різних цитат та епіграфів. Коли англійська королева Вікторія вперше прочитала книгу про Алісу, вона була в такому захопленні, що наказала негайно скупити і привезти їй все, що написав автор цієї книжки, її наказ було виконано з точністю – наступного дня перед королевою лежала купа наукових праць з математики.
Але найбільше Льюіс Керрол любив придумувати і розплутувати загадки. Візьміть хоча б таку:
Господар мав у вітальні тільки одне вікно – квадратне вікно висотою у три фути. Вікно пропускало так багато світла, що в чоловіка почали боліти очі. Тоді він викликав майстра і попросив переробити вікно так, щоб потік світла зменшився вдвічі, тобто площа вікна повинна бути вдвічі меншою. Але вікно, як і раніше, мало залишатись квадратним – в три фути висотою і в три фути шириною. Використовувати занавіски, жалюзі, кольорове скло і подібні хитрощі заборонялось. Як вдалось виконати це замовлення?
(Відповідь: Квадрат нового вікна мав вершини в серединах сторін старого)
Вед.2 .Не тільки Льюіс Керрол, а багато з видатних математиків були одночасно і письменниками. Наприклад, відомого французького математика Рене Декарта (1596 – 1650вважають одним із засновників мови французької прози. Розпочавши із «закоханості в поезію», він залишився відданим їй, і останнім його творінням була п’єса у віршах, яка була написана у Стокгольмі.
.
Вед. 1. Видатні математики – це люди високої ерудиції. Наш славетний співвітчизник, вчений, математик Михайло Васильович Остроградський (1801 – 1862) був людиною високого рівня духовної культури, досконало володів французькою мовою, був добре обізнаний з французькою літературою, не кажучи вже про російську. Але українська мова, мова його батьків, його народу була для нього найдорожчою. І хоча він міг годинами читати монологи з Мольєра та Корнелія, улюбленим його поетом був Тарас Шевченко, значну частину віршів якого він знав напам’ять . Як згадував Т.Шевченко, Остроградський приймав його у себе вдома, як рідного.
Вед. 2 Не можна не згадати і найславетнішого математика в історії людства Леонарда Ейлера (1707 – 1783). За все своє життя Ейлер написав 886 робіт з різних галузей науки. А ще він добре знав кращих письменників давнини, стародавню літературу з математики, історію всіх часів і народів, володів багатьма мовами стародавнього світу і сучасної Європи, розповідають, що він знав напам’ять «Енеїду» від початку і до кінця.
Вед. 1. Не забувають про математику і сучасні письменники. Давайте послухаємо уривок з твору Анатолія Дімарова «На коні і під конем»
Учень: «…Він уже мав колись мороку з отакою задачкою. Там розповідалося, що один господар мав три барани і чотири кози. «То скільки ж всього було голів ?» - запитувалося під кінець.
Ванько, що саме стояв біля дошки, недовго міркував. Взяв шмат крейди, звівся навшпиньки і вивів на дошці : 3 барани додати 4 кози – буде одна голова.
- Як одна? - здивувалась вчителька. – Ану порахуй: три додати чотири, то скільки буде ?
Наморщивши лоба, Ванько почав рахувати на пальцях.
- Буде сім.
- От бачиш !.. То скільки буде всього голів, коли до трьох баранів додати чотирьох кіз ?
- Один голова!
Як не билася з ним вчителька, так вона і не змогла втовкмачити , що худобу можна рахувати на голови. Ванько знав лише одного голову – сільради і не хотів поступатися цим, хоч у ступі товчи.
Повертаючись зі мною додому, він все бубонів:
- Хіба ж у баранів голови бувають ? .. То тільки в нашому селі голова – дядько Никифор.. І який дурень триматиме у себе аж три барани та ще до них чотири кози додаватиме? – хазяйнувато запитував він. – Двох баранів і чотирьох кіз треба продати, а натомість купити овець. Отоді вже їх зводити до купи…»
Вед. 2. І таких уривків з художніх творів існує безліч. А зараз переходимо до наступного нашого розділу:
Математика та живопис.
Вед.1. Людина розрізняє предмети, які її оточують за формою. Інтерес до форми будь - якого предмету може бути викликаний красою форми. А форма, в основі якої лежить поєднання симетрії та золотого перерізу, допомагає найкращому її зоровому сприйманню і появі відчуття краси та гармонії.
 Учень. Ще у епоху Відродження художники відкрили, що будь- яка картина має певні точки, що мимоволі привертають нашу увагу, так звані зорові центри. Таких точок всього чотири, і розміщені вони на відстані 3/8 та 5/8 від відповідних країв площини.
Учень. Ще у епоху Відродження художники відкрили, що будь- яка картина має певні точки, що мимоволі привертають нашу увагу, так звані зорові центри. Таких точок всього чотири, і розміщені вони на відстані 3/8 та 5/8 від відповідних країв площини.
Це відкриття у художників того часу отримало назву «золотий переріз» картини. Золотий переріз – гармонійна пропорція.
Це такий пропорційний поділ відрізка на нерівні частини, при якому довжина усього відрізка відноситься до більшої частини, як сама більша частина відноситься до меншої:
|
a : b= b : c або с : b= b : а |
|
|
|
|
Пропорція золотого перерізу - це приблизно 8:5, а ще точніше - 13:8. Художник Альбрехт Дюрер встановив, що зріст людини ділиться в золотих пропорціях лінією поясу.Талія ділить ідеальне людське тіло відносно золотого перетину. Пропорції чоловічого тіла коливаються в межах середнього відношення 13:8 і трохи ближче підходять до золотого перерізу, ніж пропорції тіла жінок (8:5), які змушені "урівнювати" фігуру за рахунок підборів.
Вед. 2. Історик і мистецтвознавець Олексій Карпович Дживелегов писав:
«Живопис приходив до математики через учіння про перспективу і через оптику , скульптура – через учіння про пропорції , архітектура – через учення про масу й вагу тіл і через те ж учіння пропорції. Мистецтво ставало наукою. Ніхто не почував цього так ясно і сильно, як Леонардо да Вінчі, і недарма в його творчості мистецтво й наука стали двома сторонами одного й того самого, чимось неподільним.»
Учень:
Саме вивченню «золотого перерізу» приділяв багато своєї уваги великий італійський художник, учений Леонардо да Вінчі .Особистість Леонардо да Вінчі – одна із загадок у історії. Сам учений говорив: «Нехай ніхто, не будучи математиком, не наважиться читати мої праці». Він дістав славу талановитішого художника, великого ученого, генія, що передбачив багато винаходів, які не були впроваджені майже до ХХ ст.
Його картина «Таємна вечеря» демонструє нам використання гармонійної пропорції «золотого перерізу».
Портрет Мони Лізи (Джоконди) багато вже років притягує увагу дослідників, які виявили, що композиція малюнку базується на золотих трикутниках, що є частинами правильного зірчастого п’ятикутника.
Існує дуже багато версій про історію цього портрету. Ось одна з них.
«Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.
Сказка
Жил-был один бедный человек, было у него четыре сына: три умных, а один из них и так, и сяк. И вот пришла за отцом смерть. Перед тем, как расстаться с жизнью, он позвал к себе детей и сказал: “Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастья. Пусть каждый из вас чему-нибудь научится, чтобы мог кормить сам себя”. Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи. Пришел первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел ее: как искусный мастер он сшил для нее красивую шелковую одежду. Третий сын украсил женщину золотом и драгоценными камнями – ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и еще умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: “Ты должна быть моей женой”. Но женщина ответила: “Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями.
А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь”.
Кончив сказку, Леонардо взглянул на Монну Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано – художник пробудил равнодушную статую; улыбка блаженства, медленно исчезая с ее лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно ее храня, не может сдержать торжество. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель...»
Учень: А зараз до вашої уваги картина І.І. Шишкіна «Сосновая роща»
|
На цій відомій картині з очевидністю проглядаються мотиви золотого перерізу. Яскраво освітлена сонцем сосна (що стоїть на першому плані) ділить довжину картини за золотим перерізом. Праворуч від сосни – освітлений сонцем пагорб. Він ділить за золотим перерізом праву частину картини по горизонталі. Ліворуч від головної сосни знаходиться безліч сосен - при бажанні можна з успіхом продовжити поділ картини за золотим перерізом и далі. |
|
|
|
|
Учень:
Працюючи над картиною «Бояриня Морозова», російський художник Василь Суриков мав викликати у глядача ілюзію руху саней, в яких везуть розкольницю. Чуття підказувало, що сани «поїдуть», тільки коли полоззя помістити на строго визначеній відстані від рами. І художник шукав її, пробуючи різні варіанти. Він записав тоді: «У русі є живі точки, а є мертві. Це справжня математика. Фігури, що сидять на санях, тримають їх на місці. Треба було знайти відстань від рами до саней, щоб пустити їх у хід. Трохи менша відстань, - сани стоять.» Саме пропорції «золотого перерізу» пояснюють таємницю емоційного впливу картини «Бояриня Морозова» на глядача, таємницю «чарівної сили» живопису.
Вед.1
А зараз давайте ближче познайомимося із Альбрехтом Дюрером (1471 – 1528). Живописець, гравер, гуманіст, учений, Дюрер був першим художником у Німеччині, який вивчав математику і механіку, будівельну і фортифікаційну справи. Він перший у Німеччині намагався застосувати в мистецтві свої наукові знання в галузі перспективи і пропорцій.
Ось найзнаменитіша гравюра художника «Меланхолія»
А.Дюрер «Меланхолія»
На цій гравюрі Меланхолія оточена атрибутами геометрії та архітектури, і , мабуть думка про безмірність знання повергає її у бездіяльність і відчай. На гравюрі розв’язана складна геометрична задача побудови перспективи додекаедра, а у правому верхньому кутку зображений магічний квадрат, складений з перших чисел натурального ряду, сума яких у будь якій стрічці, стовпці або діагоналі є стала (34).
Математика має справу з абстракціями, які створюються у нашій свідомості. І говорячи сьогодні про зв’язок математики та живопису, не можна не згадати про гравюри відомого голландського художника Моріса Корнеліуса Ешера (1898 – 1972). На своїх гравюрах художник показав, як люди можуть давати неправильне тлумачення інформації, яка надходить до органів чуттів, коли оцінюють розміри тіл, інтервали часу, положення предметів у просторі, їх колір. Саме ці особливості сприймання нами тривимірного простору з дивовижною майстерністю використав художник.
Вед.2
Побачити, як математика пов’язана з мистецтвом, можна на прикладі архітектури.
(Слайд «Математика і архітектура»)
Йдучи вулицями міста, можна спостерігати, як геометричні форми використовуються в архітектурі. Подивимось на найвідоміші архітектурні пам’ятки світу: … (слайди)
Ми бачимо колони, арки, ніші, фризи, ажурні бароківські ліплення складної форми. Лише досконале знання архітектором математики дає можливість поєднати здавалося б прості геометричні форми (куб, паралелепіпед, циліндр, еліпс, коло) у складну музику вишуканих будівель.
Результат роботи архітектора повинен бути точним. Його перспективний малюнок повинен відповідати правилам геометрії, зокрема нарисної. Отже , ні один архітектор не обійдеться без знання масштабу, пропорції, симетрії.
Саме симетрія – це врівноваженість, упорядкованість, краса, довершеність, доцільність. Будь-яка архітектурна споруда використовує симетрію. Симетрія використовується в будівництві, техніці і в повсякденному житті.
Вед.1
Остання наша сторінка «Математика і музика»
(слайди…)
Мабуть, кожен з вас зараз подумав, який же ж зв’язок може бути між математикою - мудрою царицею всіх наук, та музикою? Як можуть взаємодіяти, такі, зовсім різні , людські культури? Сьогодні, я пропоную вам знайти відповіді на ці запитання, довести, що зв’язок між музикою і математикою існує.
Вед.2
Музика - найбільш суб'єктивна з наук, і найбільш абстрактно логічна з мистецтв.Бо музика - то є Гармонія Душі.
Людство винайшло дві універсальні гармонічні дисципліни-абстракції, одна з яких опікується логікою й чіткістю сталих законів, а друга - емоційним змістом і життям без кордонів. Перша - математика, друга - музика.
Вед.1
Англійський математик Джеймс Сільвестр говорив:
«Чи не може музика бути описаною як математика почуттів, а математика як музика розуму ? Так, наприклад, музикант відчуває музику, математик розуміє музику, - музика це мрія, математика - ділове життя – кожна повинна дістати своє завершення від другої, коли людський розум, піднесений до досконалого зразка, сяятиме далі, уславлений у якомусь майбутньому Моцар том–Діріхле чи Бетховеном–Гауссом – такий союз виразно виявляється в генії і працях Гельмгольца!»
Учень:
Ідея про можливість побудови числової моделі світу була покладена Піфагором в основу його теорії музики. Про Піфагора відома така історія
«Однажды, размышляя над проблемой гармонии, Пифагор проходил мимо мастерской медника, который склонился над наковальней с куском металла. Заметив различие в тонах между звуками, издаваемыми различными молоточками и другими инструментами при ударе о металл, и тщательно оценив гармонии и дисгармонии, получающиеся от комбинации этих звуков, Пифагор получил первый ключ к понятию музыкального интервала. Он вошел в мастерскую и после тщательного осмотра инструментов и прикидывания в уме их вес вернулся в собственный дом, сконструировал балку, которая была прикреплена к стене, и приделал к ней через равные интервалы четыре струны, во всем одинаковые. К первой из них прикрепил вес в двенадцать фунтов, ко второй - в девять, к третьей - в восемь, и к четвертой - в шесть фунтов. Эти различные грузы соответствовали весу молотков медника. Пифагор обнаружил, что первая и четвертая струны, когда звучат вместе, дают гармонический интервал октавы, потому что удваивание веса имело тот же эффект, что и укорачивание струны наполовину. Натяжение первой струны было в два раза больше, чем четвертой струны, и, как говорят, их соотношение равно 2:1, или двукратное. Подобным же рассуждением он пришел к заключению, что первая и третья струны дают гармонию квинту. Натяжение первой струны было в полтора раза больше, нежели третьей струны, и их соотношение было 3:2, или полуторное.»
Одже, Піфагор винайшов, що якісні відміни в звучанні струн обумовлюються чисто кількісними відмінностями, а саме натягом струн. Одночасне звучання двох струн буде приємне для слуху якщо їх натяги відноситься, як 1:2, або 2:3, або 3:4, що відповідають музичним інтервалом в октаву, квінту і кварту.
Вед.2 День відкриття цього факту можна назвати день народження математичної фізики.
А. Енштейн писав: “Ми відкрили щось подібне на коливання струни і атому, що випромінює промені, така система частин веде себе подібно до малого акустичного інструменту, в якому виробляють стоячі хвилі”.
Вед.1
А у листі Х.Гольдбаху у 1712 році великий німецький математик Г.Лейбніц писав: «…Ми в музиці не рахуємо далі п’яти, подібно до народів, які в арифметиці не пішли далі трьох… Всі наші інтервали – це відношення, складені з відношень між двома числами 1, 2, 3, 5… Музика – це прихована математична вправа душі, яка не вміє рахувати…»
Вед.2
Німецький природознавець Г.Гельмгольц говорив:
« У мене завжди викликав жвавий інтерес той дивний факт, що в ученні про звук – у фізичній і технічній основі музики, яка за допомогою короткочасної швидкоплинної дії викликає в нашій душі такі незрозумілі настрої, що не піддаються описові, - виявилась такою корисною математика – наука найстрогішого і чистого мислення.
Вед.1 Майже всі справжні композитори та музиканти розуміли, що в основі музики лежить математика.
Музика не може існувати без нот. Ноти – азбука музиканта. Кожна нота має свою тривалість. Є ноти цілі, половині, четвертні, восьмі, шістнадцяті.
Доведено, що діти, які займаються музикою легше засвоюють
математику. У них добре розвинуті просторова і творча уяви, інтуїція.
Учень.
Математично тривалість нот записують за допомогою звичайних
дробів. Ціла – 1, половина -1/2, четвертна -1/4, восьма – 1/8, шістнадцята – 1/16.
|
математика |
Музика ( тривалість нот) |
|
Ціле число (торт) |
Ціла нота |
|
Ділимо пополам (половина торта) |
Половина цілої ноти - половинна |
|
Ділимо торт на чотири частини (отримуємо одну четверту) |
Ділимо цілу ноту на 4 частини – ( четвертна) |
|
На вісім ( одна восьма) |
На вісім ( восьма , восьмушка) |
|
На шістнадцать ( одна шістнадцята) |
На шістнадцять ( Шістнадцята) |
Отже, ми бачимо, ноти позначаються з допомогою знаків, а їх тривалість визначається математичним рахунком.
А чи існують у музиці математичні дії? « Музичне множення»
записують так: після знака ноти ставлять крапку, це означає, що тривалість ноти
потрібно збільшити в півтора рази.
♪♪ - цей запис є «музичне додавання»- збільшення тривалості двох однакових за висотою нот.
Пропонуємо вам виконати музичні сувеніри-приклади, де числа
зашифровані тривалістю нот.
Вед.1
Далеко не всі композитори мали абсолютний слух. А , наприклад, Людвігу Ван Бетховену не було ще й тридцяти років, коли він відчув перші ознаки глухоти, яка згодом відокремила його від навколишнього світу і, навіть , наштовхнула його на думку про самогубство. Врятували його від трагічної смерті любов до музики, любов до життя, впевненість у тому, що перемагає той, хто бореться. І уявіть собі, як не знаючи математичних закономірностей побудови музики, можна було б створити такі шедеври як«Місячна соната» або один з найвідоміших творів Бетховена – симфонія № 5.
Вед.2 Великий композитор Вольфганг Амадей Моцарт, пишучи свої вальси і менуети, використовував заснований на теорії ймовірностей «механічний пристрій» - кубик. Про нього А.Моль писав: «Винайдений Моцартом спосіб компонувати мелодію за допомогою гри в кості над спеціальною таблицею, яка визначає вибір наступного такту створюваної п’єси, свідчить про те, що великі композитори чітко усвідомлювали роль випадковості в загальній побудові музичного повідомлення», тобто роль теорії ймовірностей – Одного з розділів математики.
Вед.1
Зараз математики почали розглядати музичну партитуру як графік, на якому по вертикалі відкладається висота звуку, а по горизонталі – час. Інші характеристики – тональність, тривалість звучання, паузи, ритм тощо – додаються, але за допомогою додаткових символів . Тепер у нас є докази того, що кожний акорд можна представити не просто за допомогою довільних знаків на розлінованому папері, але і як точку в геометричному просторі.
Вед.2 Ще раз згадаємо про славетного математика Леонарда Ейлера. Він полюбляв слухати музику, яка дещо відволікала його від напруженої праці і навіть писав трактат про нову теорію музики, про який говорили, що в ньому багато музики для математиків і водночас надто багато математики для музикантів.
Вед.1
Професор Київського Державного університету ім. Т.Г. Шевченка Микола Іванович Кованцов писав:«Ейлер у математиці – це Моцарт у музиці, Пушкін у поезії, Мікеланджело в живопису»
Вед.2 Ми , звичайно, моли б знайти ще багато прикладів взаємодії математики та мистецтва. Тепер кожен з вас може впевнено про це заявити та відстояти свою точку зору.
І на завершення давайте послухаємо уривок з одного з творів В.А.Моцарта, це прекрасний вальс «Вальс Квітів» (звучить музика…)
Використані матеріали:
- Статті з газети «Математика» в-ва «Шкільний світ» 2008-2009 рр.;
- «Про математику і математиків». Висловлювання видатних діячів минулого і сучасності. Упорядники А.С.Зоря, С.М.Кіро. К., «Радянська школа», 1981 р.
- Ресурси Internet ;
- Фрагменти презентації «Математика і музика» Дмитрук А.В., учителя математики Стрижавської СЗШ № 1 Вінницького району.
1

Н. Вінер








про публікацію авторської розробки
Додати розробку