Позакласний захід "СІРНИКИ - НЕ ІГРАШКА"

Математика, 5-6 клас

СІРНИКИ - НЕ ІГРАШКИ?

(година цікавої математики)

 

Математика завжди була складною наукою для опанування її школярами. Звідси й завдання, яке стояло і стоїть перед учителем, -  розкрити багатоманітний її світ, показати можливості застосування математики серед повсякденних речей.

Задачі із сірниками завжди були популярними серед вчителів математики. Розв’язування таких задач  допомагає розвивати кмітливість і уяву школярів, що є дуже важливим при вивченні математики.

 

Мета: популяризувати математичні знання;

формувати уявлення про багатоманітний світ математики;

розвивати уяву, кмітливість, логічне мислення, творчі здібності учнів;

виховувати вміння працювати в парі, уважність.

 

Обладнання: коробки сірників (із розрахунку одна коробка на кожну парту), бонуси-фішки різного кольору: зелені – за колективні відповіді, сині – за індивідуальні відповіді.

 

ХІД заходу:

 

 

Лежать у порядку дерев’яні малятка,

Білі, здорові, всі чорноголові.

Учитель: Правильно, це – сірники. Сьогодні для проведення уроку будемо користуватися сірниками.

 

Чи знаєте ви що:

1.              Англійський фармацевт Джон Уокер придумав свій винахід, як це часто буває, зовсім випадково. У 1826 році він, оскільки був фармацевтом , змішував хімікати за допомогою палиці. На кінці цієї палиці утворилася засохла крапля . Щоб прибрати її, він чиркнув палицею по підлозі. Спалахнув вогонь! Він став експериментувати, і 7 квітня 1827 відбулася перша комерційна угода: Уокер продав адвокату Ніксону перші сірники
2.              Однак Уокер, демонстрував своє відкриття всім підряд, так і не спромігся його запатентувати. А ось хлопець на ім'я Сем'юел Джонс, який якось був присутній при такій демонстрації, усвідомив ринкову вартість винаходу. Він назвав сірники « люціферчікі » і став продавати їх тоннами, незважаючи на те, що з «люціферчікамі» були пов'язані деякі проблеми - вони погано пахли і при загорянні розсипали навколо хмари іскор .
3.              У 1910 році американська компанія Diamond Match першою отримала патент на безпечні для здоров'я сірники. Важливість цього винаходу була настільки велика, що президент США Вільям Тафт публічно звернувся до власників патенту і попросив їх відмовитися від авторських прав. Компанія погодилася і 28 січня 1911 відмовилася від усіх прав на свій винахід. Тому сьогодні сірники належать фактично всім.
4.              Народ полюбляє виготовляти із сірників????

А сьогодні на заході ми з вами будемо розвивати логічне мислення, розв’язувати задачі з сірниками

 

Згадуємо римську нумерацію у відповідності її до арабської, яку використовують на уроках математики.

І – 1;

V – 5;

Х – 10;

L – 50;

C – 100;

D – 500;

M – 1000.

Якщо пишемо числа більші або менші від вказаних, то користуємося принципом додавання або віднімання: ІV відповідає арабському числу 4 (на один менше від п’яти) , VІ – арабське 6 (на один більше від п’яти), ІХ – 9, ХІІ – 12,  ХL – 40,  LХХХ – 80 тощо.

Усні завдання на закріплення (учні відповідають індивідуально, за правильну відповідь отримують бонус від учителя):

- Зобразити за допомогою двох сірників як можна більше римських чисел (на виконання завдання 30 секунд, бонус - за кожне правильно складене число).

Відповідь: І, ІІ, V, Х, L.

- Зобразити за допомогою трьох сірників як можна більше римських чисел (на виконання завдання 30 секунд, бонус - за кожне правильно складене число).

Відповідь: ІІІ, ІV, VІ, ІХ, ХІ, LІ, С.

 

Для розминки пропонуємо таку задачку:

Три сірники лежать на столі. Як прибрати середній сірник із середини, не торкаючись його?

Відповідь: Один з крайніх сірників кладуть поряд з іншим крайнім (так середній опиняється з краю).

Учень, який запропонував правильну відповідь, отримує бонус-фішку від учителя.

Учитель: Отже, ми сьогодні розв’язуємо задачі із сірниками. Але не забуваємо правило, що необережне поводження із сірниками може стати причиною пожежі.

 

Робота на заході відбувається у парах. Пара, яка першою розв’язала задачу, отримує два бонуси, а пари, які виконали завдання вірно і вклалися у визначений час – один бонус.

На розв’язання кожного завдання учитель відводить не більше однієї хвилини.

 

1. Як зробити з двох сірників десять, не ламаючи їх?

Відповідь: Скласти з них римське число Х.

 

2. Чи можна з трьох сірників зробити шість, не ламаючи їх?

Відповідь: Так, необхідно з них скласти римське число VІ.

 

3. У даній неправильній рівності необхідно перекласти один сірник, щоб рівність стала правильною: VІ + ІV = ХІІ.

Відповідь: VІІ + V = ХІІ.

 

4. Чи можна з чотирьох сірників зробити сім, не ламаючи їх?

Відповідь: Так, необхідно з них скласти римське число VІІ.

 

5. Як з 8 сірників зробити три?

Відповідь: Скласти з них слово «три».

 

6. Візьміть 12 сірників і викладіть з них таку «рівність»: VІ – ІV = ІХ. Рівність, як бачимо, неправильна, бо 6 - 4 не дорівнює 9. Перекладіть один сірник так, щоб утворилась правильна рівність.

Відповідь: Можливі два варіанти: V + ІV = ІХ або VІ + ІV = Х.

 

7. Як з 13 цілих сірників, кожний з яких має довжину 5 см, покладених один біля одного, скласти метр?

Відповідь: Скласти слово «метр».

 

8. У даній неправильній рівності необхідно перекласти один сірник, щоб рівність стала правильною: Х - ІХ = VІ.

Відповідь: ХІ – ІХ = ІІ.

 

9. Додати до чотирьох сірників п’ять так, щоб утворилося сто. Спробуйте знайти два розв’язки.

Відповідь: Скласти із сірників слово «сто», а також можна скласти число 100.

 

10. У даній неправильній рівності необхідно перекласти один сірник, щоб рівність стала правильною: VІІІ + ІV = ХVІІ.

Відповідь: VІІІ + ІХ = ХVІІ.

 

11. З 9 сірників скласти 6 квадратів (можна накладати один сірник впоперек іншого).

Відповідь:

 

 

 

 

 

12. З 12 сірників викладено 4 однакових квадратів, як на малюнку, при цьому утворився ще один додатковий квадрат (великий). Необхідно прибрати 2 сірники (решту не займати), щоб утворилося два нерівних квадрати.

Відповідь:

 

 

13. З 10 сірників викласти 3 квадрати.

Відповідь:

 

 

14. У даній неправильній рівності необхідно перекласти один сірник, щоб рівність стала правильною: Х + Х = І.

Відповідь: ХІ – Х = І.

 

Завдання 15. Переставити один сірник так, щоб рівність була пра­вильною.

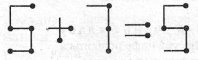
Відповідь

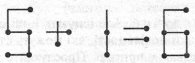
 Відповідь

Завдання 16. Переставити 4 сірни­ки так, щоб утворилось два квад­рати.

Відповідь

 

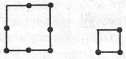
Завдання 17 Переставити 2 сірни­ки так, щоб утворилось 5 рівних квадратів.

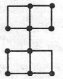
Відповідь

Завдання 18. Переставити 1 сірник так, щоб рівність була правиль­ною.

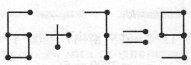
Відповідь

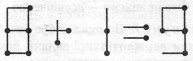
Завдання 19 Дванадцять сірників лежать так, як показано на малюнку. Скільки тут квадратів?
     Виконаєте наступні завдання:
1) перекладете 3 сірника так, щоб утворювалося 3 рівних квадрата;
2) перекладете 4 сірника так, щоб утворювалося 10 квадратів.

 

 

Відповідь на перше завдання:

 

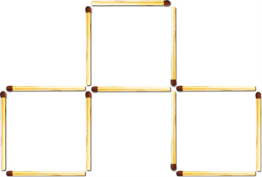
Відповідь на друге завдання:

 

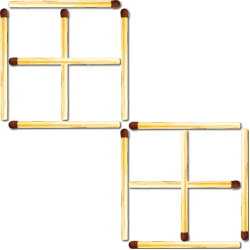
Завдання 20 Перекладіть 3 сірника так, щоб стріла поміняла свій напрямок на протилежний.

Завдання 21   І "келих" (див. лівий малюнок), і "чарка" (див. правий малюнок) складені із чотирьох сірників. Усередині кожної "посудини" - вишенька. Як потрібно перемістити "келих" і "чарку", переклавши по два сірники в кожному з них, щоб вишеньки виявилися зовні?

          

 

 

   

 

 

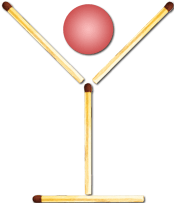
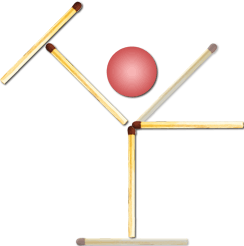
V. Підсумки заходу

Учні підраховують кількість отриманих за захід фішок, називають цю кількість учителю, який таким чином визначає найкмітливішу пару та найкмітливішого учня на уроці.