Прес-конференція банку "Первісна"
Прес-конференція банку «Первісна»![]()
(навчальне заняття з алгебри і початків аналізу). 11 клас
Мета: закріпити знання студентів про первісну; формувати уміння і навички
обчислення первісних, користуючись таблицею первісних та правилами
знаходження первісних;
розвивати логічне мислення, творчу активність, вміння самостійно
застосовувати набуті знання, активізувати пізнавальну діяльність;
формувати навички правильної математичної мови.
Обладнання: проектор, таблиця первісних.
Епіграф: Яка радість особливо велика? Коли вдається досягти бажаного.
(Фалес Мілетський, давньогрецький учений (VI ст. до н.е.))
«Математика – це мова плюс міркування, це наче мова й логіка разом.
Математика – це знаряддя для міркування.» Р. Фейнман
Не достатньо мати гарний розум, необхідно ще вміти його
використовувати». (відомий французький математик Р.Декарт)
Хід заняття
І. Повідомлення теми і мети заняття, мотивація навчальної діяльності.
Життя – найчарівніший дар природи, але, щоб воно приносило радість, потрібно навчатись працювати захоплено, прагнути полегшити свою працю та вдосконалити її звичайні форми.
Сьогодні ми з вами перенесемось у зачарований науковий світ. Уявімо, що ми на прес-конференції банку, де обговорюється питання «Первісна», її обчислення, користуючись таблицею та правилами обчислення первісної.
Ми з вами знаходимося біля дверей нашого банку, спробуємо відімкнути кодовий замок установи. Для цього ви маєте назвати первісну для кожної з даних функцій.
1) ![]()
![]() 2)
2) ![]() 3)
3) ![]()
4) ![]() 5)
5) ![]() 6)
6) ![]() .
.
2. Математичний диктант.
Запишіть первісні для функцій:
1) х7; 2)![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6) ex;
; 6) ex;
7) πx; 8)![]() ; 9)
; 9) ![]() ; 10) cos х; 11) sin х; 12)
; 10) cos х; 11) sin х; 12)![]()
Відповідь: 1) ![]() +С; 2) ln|x| +C; 3) –
+С; 2) ln|x| +C; 3) –![]() +C; 4)
+C; 4) ![]() +C; 5)
+C; 5) ![]() +C; 6) ex + C; 7)
+C; 6) ex + C; 7) ![]() +C; 8) tgx+C; 9) –ctgx + C; 10) sinx + C; 11) - cosx + C; 12)
+C; 8) tgx+C; 9) –ctgx + C; 10) sinx + C; 11) - cosx + C; 12) ![]() + C.
+ C.
Отже, двері банку «Первісна» відкриті і ми можемо розпочати наш робочий день. Оскільки наш банк відкрито недавно, то не вся громадськість знає про роботу нашої установи. Отже, щоб привернути увагу громадськості, запросити клієнтів до нашого банку, ми проведемо прес-конференцію для представників засобів масової інформації.
На нашій конференції присутні кореспонденти, журналісти різних науково-популярних газет, журналів, телепередач тощо.
ІІ. Повторення вивченого матеріалу (відповіді на запитання журналістів).
- Газета «Банківська справа».
У мене запитання до директора банку. Поясніть, будь ласка, що означає назва вашого банку «Первісна» та як називається операція знаходження первісної. Дякую за відповідь.
- Журнал «Історія і право».
Скажіть, будь ласка, хто з математиків відкрив інтегральне числення. Дякую за відповідь.
Відповідь: Інтегральне числення виникло з потреб обчислення площ плоских фігур і об'ємів довільних тіл. Ідеї інтегрального числення беруть свій початок у роботах стародавніх математиків. Свій вклад в розвиток інтегрального числення зробили Архімед, німецький астроном Йоган Кеплер (1571-1630), італійський математик Кавальєрі (1598-1647).
Ідеї Кеплера, Кавальєрі та ін. вчених стали грунтом, на якому І.Ньютон і Г.Лейбніц відкрили інтегральне числення. Розвиток інтегрального числення продовжили Л.Ейлер та російський математик П.Л.Чебишев (1821-1894), який розробив способи інтегрування деяких класів ірраціональних функцій.
Сучасне означення інтеграла належить О.Коші. Термін «інтеграл» був запропонований у 1690 році братом Й.Бернулі – Якобом Бернулі (1654-1705).
- Юридична газета. У нас з колегою виникло непорозуміння щодо кількості первісних для даної функції. Допоможіть, будь ласка. А ще ми хочемо знати які властивості має первісна.
- Телепередача «Успішний бізнесмен».
Я гадаю, що під час розв'язування вправ мені потрібно буде користуватись правилами знаходження первісних. Нагадайте нам, будь ласка, ці правила. Дякую за відповідь.
Газета «Аргументи і факти».
Я хочу провести тестування всіх присутніх, щоб більше дізнатись про співробітників банку.
Тестові завдання
- Яка з наведених функцій є первісною функції f (x) = x4?
А) F(x) = 4x3; Б) F(x) =![]() ; B)
; B) ![]() ; Г) F(x) = x5.
; Г) F(x) = x5.
2. Знайдіть загальний вигляд первісної функції f (x) = x – 4:
-
x2 – 4x + C; Б)
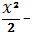 4x + C; В)
4x + C; В) 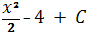 ; Г) x2 – 4 + C.
; Г) x2 – 4 + C.
3. Укажіть загальний вигляд первісної функції f (x) = 2x3 + 6x:
А) 6x + 6 + C; Б)![]() ; В) x4 + 2x3 + C; Г) 4x4 + 3x2 + C.
; В) x4 + 2x3 + C; Г) 4x4 + 3x2 + C.
4. Яка з поданих функцій є первісною функції f (x) = 3x?
А) ![]() ; Б) F(x) = 3x ln3; В) F(x) = 3x; Г)
; Б) F(x) = 3x ln3; В) F(x) = 3x; Г) ![]()
5. Яка з наведених функцій є первісною функції ![]() :
:
A) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
6. Укажіть загальний вигляд первісної функції f(x) = 10x4 - 6x.
А) 2x5 – 4x2 + C; Б) 2x5 – 3x2 + C; В) 5x5 – 4x2 + C; Г) 40x3 – 6 + C.
Викладач. Повторення теоретичного матеріалу закінчено. Дякую всім за участь. Отже, журналісти зібрали необхідний матеріал для розв'язування вправ. Прошу зробити перерву в нашій прес-конференції. Розглянемо декілька вправ на закріплення правил знаходження первісних.
- Знайти первісну функції (усно):
- Розв’язування вправ на знаходження первісної, яка задовольняє дану умову:
-
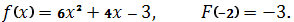
-
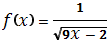 , графік первісної проходить через точку А(3;1).
, графік первісної проходить через точку А(3;1).
Самостійна робота.
Варіант 1
- Для функції f(x) = 3х2 знайдіть первісну, графік якої проходить через точку
А(0; 1). (3 бали)
2. Знайдіть загальний вигляд первісних для. функцій:
a) f(x) = cos 2x + sin Зх; б) f(x) = ![]() . (4 бали)
. (4 бали)
3. Знайдіть невизначені інтеграли: a) ![]() ; б)
; б) ![]() . (4 бали)
. (4 бали)
Варіант 2
1. Для функції f(x) = 4х3 знайдіть первісну, графік якої проходить через точку
А(0; 1). (3 бали)
2. Знайдіть загальний вигляд первісних для функцій:
a) f(x) = ![]() ; б) f(x) =
; б) f(x) = ![]() . (4 бали)
. (4 бали)
3. Знайдіть невизначені інтеграли: a) ![]() ; б)
; б) ![]() . (4 бали)
. (4 бали)
Відповідь: В-1. 1. F(x) = x3 + 1. 2. a) F(x) = ![]() sin2x –
sin2x – ![]() cos3x + C;
cos3x + C;
б) ![]() . 3. а)
. 3. а) ![]() ; б) tg(3x - 1) + С.
; б) tg(3x - 1) + С.
В-2. 1. F(x) = х4 + 1, 2. a) F(x) = ![]() tg 2х + ctg х + С;
tg 2х + ctg х + С;
б) ![]() . 3. a)
. 3. a) ![]() ; б) sin (3х + 2) + С.
; б) sin (3х + 2) + С.
А зараз продовжимо нашу прес-конференцію.
Відповідаємо на запитання журналістів.
- Видавництво «Шпаргалка студенту» просить надати допомогу в розв’язання вправи.
Для функції ![]() знайти первісну F(х), графік якої проходить через точку А(
знайти первісну F(х), графік якої проходить через точку А(![]() ).
).
- Телепередача «Віриш? Не віриш?» просить перевірити виконання вправ:
Видавництво «Екзамен без проблем» має багато запитань до нашого банку. Отже, зараз усі займемося підготовкою відповідей видавництву.
Знайдіть первісну функції, графік якої проходить через вказану точку.
-
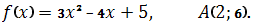
-
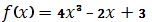 , A(1;8).
, A(1;8).
-
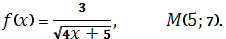
-
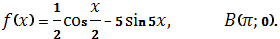
Домашнє завдання.
Радіопередача «Роблю сам» чекає на письмові відгуки про виконання завдань.
-
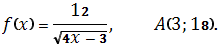
-
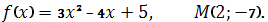
-
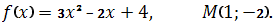
-
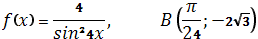 .
.
![]()


про публікацію авторської розробки
Додати розробку
