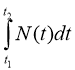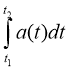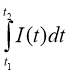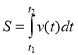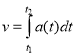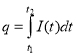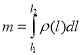Урок. Застосування похідноі та інтегралу у фізиці

 

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ВІННИЦЬКИЙ  КОЛЕДЖ

НАЦІОНАЛЬНОГО  УНІВЕРСИТЕТУ ХАРЧОВИХ ТЕХНОЛОГІЙ

 

 

 

 

 

 

 

 

 

 

 

Методична розробка відкритого заняття

на тему: 

„ Застосування похідної та інтегралу у фізиці”

 

 

 

 

 

 

Викладач    Бараболя М.М.

 

 

 

 

Вінниця, 2019

 

Тема заняття.  Застосування похідної та інтегралу у фізиці .

 

Методична спрямованість: використання інтерактивних технологій навчання для активізації пізнавальної діяльності студентів

 

Мета заняття:

Дидактична: повторити та узагальнити вивчені раніше відомості диференціального та інтегрального числення, формувати вміння застосовувати здобуті знання в нестандартних умовах, зокрема, у задачах з фізики.

Розвиваюча:    розвивати  вміння узагальнювати цілісну систему, вміння реалізувати практичні зв’язки  курсу математики і фізики, розвивати навички самостійного прийняття рішень, розвивати пізнавальний інтерес, навички колективної праці;

Виховна:   сприяти глибокому засвоєнню знань фізики і математики через встановлення міжпредметних  зв’язків  засобами диференціального та інтегрального числення, формувати практичні зв’язки  наукового  розуміння  законів, взаємозв’язків явищ у природі за допомогою розв’язування задач;

 Методичне та матеріальне забезпечення заняття: презентації задач в форматі Power Point, плакати,  комп’ютер, мультимедійний проектор, роздатковий матеріал.      

Студенти повинні знати: студенти повинні знати поняття похідної, геометричний та фізичний зміст похідної функції.

Студенти повинні вміти:  вміти розв’язувати фізичні задачі з використанням похідної та інтегралу.

Студенти повинні мати навички:  обчислювати похідні, інтеграли функцій, розв’язувати фізичні задачі.

Застосовані методи навчання:   репродуктивна бесіда, робота в групах, «Мозковий штурм», захист проектів,  тестовий контроль, демонстрація у Power Point.

Ключові слова: функція, похідна, інтеграл, швидкість,шлях, сила струму.

Міжпредметні зв’язки:

забезпечуючі: історія, фізика, математика

забезпечувані: електротехніка, технічна механіка, нарисна геометрія

Випереджувальні завдання: студенти поділені на три групи: «ПОХІДНА», «ІСТОРІЯ», «ІНТЕГРАЛ», які готують доповіді «Практичне застосування похідної та інтегралу у фізиці»

Зміст завдань для груп

1.          Історичні відомості (студенти готують інформацію про виникнення диференціального та інтегрального числення та їх розвиток, про біографію та праці їх творців тощо).
2.              Застосування диференціального числення до розв'язування фізичних задач.
3.              Застосування інтегрального числення до розв'язання прикладних фізичних задач .

Література:

1. Бурда М.І., Дубинчук О.С., Мальований Ю.І. Математика (підручник для  навчальних закладів освіти гуманітарного профілю), 10-11 кл. –  К.: Освіта, 2010.
2.               Є.П. Нелін, О.Є.Долгова.            Алгебра і початки аналізу. 11 клас. – Х, Світ дитинства, 2010.
3.               Г.П.Бевз, В.Г.Бевз.     Математика, 11 – К.Генеза, 2011.

 

 

 

 

 

 

 

 

 

Хід заняття

I. Організаційний момент.(2хв.)

ІІ. Оголошення теми та мети заняття. ( 3 хв)

Фізик:Відомий італійський вчений Галілей говорив: «Філософія написана в тій величній книзі, яка завжди відкрита в нас перед очима (я маю на увазі  Всесвіт), але яку неможливо зрозуміти, якщо заздалегідь  не вивчити її мову».

 

Математики: Її мова – це мова математики. Математика здавна має репутацію найточнішої галузі знань і є надійним знаряддям розкриття таємниць природи.

 

Фізик: Навіть знаменитий Ейнштейн писав: «Наш досвід переконує нас, що природа – це реалізація найпростіших математичних ідей».

 

Математик: Вже минуло понад 4 тисячі років відтоді, як давньогрецький писар Ахмес переписав з ще більш раннього рукопису обіцянку за допомогою математики «навчити досконалого й ґрунтовного дослідження всіх речей, розуміння їхньої суті,  пізнання всіх таємниць…».

 

Фізик: І, як сказав добре відомий вам Рене Декарт: «Той, хто  серйозно прямує до пізнання істини, не повинен займатися якоюсь однією наукою, бо всі вони тісно взаємопов’язані».

 

Математик: Ну що ж, сподіваюсь, що  за допомогою наших великих знаменитих вчених, вислови яких ми цитували, переконали  присутніх в доцільності проведення заняття щодо застосування математики у фізиці.

Сьогоднішнє заняття присвячене застосуванню диференціального та інтегрального числення  при розв’язуванні фізичних задач.

Зробити наголос на важливість професійних компетенцій

техніка-електромеханіка:

•     робота в колективі,
•     готовність і здатність навчатись самостійно,
•     здатність орієнтуватися в інформаційному полі,
•     готовність вирішувати складні завдання.

III. Актуалізація знань (15 хв.)

1. Розгадування кросворду. За кожну правильну відповідь по 1балу.

1. Інтервали, в яких графік функції опуклий вгору або вниз, називається інтервалами….

2. Як поводить себе функція на заданому інтервалі, якщо її похідна в цьому інтервалі додатна?

3. Величина миттєвої швидкості в момент часу t₀ дорівнює значенню похідної від шляху S(t) в точці t₀    Який зміст похідної виражено?

4. Процес знаходження похідної

5. Як поводить себе функція на заданому інтервалі, якщо її похідна в цьому інтервалі від’ємна?

6. Внутрішні точки області визначення функції y=f(x), у яких похідна дорівнює нулю… називаються точками…

7. Якщо похідна змінює свій знак з плюса на мінус, то це точка…

Відкриттів зроблено багато, давайте повторимо основні теоретичні моменти,розгадавши кросворд :Н

 

 

 

 

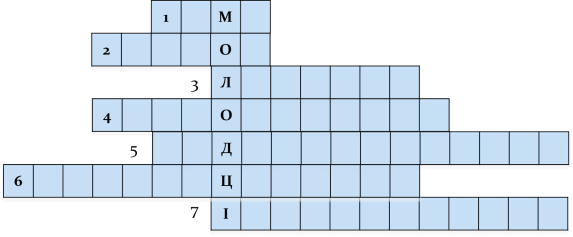ЕГРАЛ

F(х)

1. Першу букву якого слова нагадує знак інтеграла? (Summa - сума)

2. Хто із відомих математиків-фізиків розглянув фізичний зміст інтеграла? (Ньютон)

3. Хто із відомих математиків розглянув математичний зміст інтеграла? (Лейбніц)

4. Як називається трапеція, площу якої ми знаходимо за допомогою визначеного

інтеграла? (Криволінійна)

5. Як називається функція, яка стоїть пі знаком інтеграла? (Підінтегральна)

6. Як називається множник dx в підінтегральному виразі? (Диференціал)

7. Як називається операція обернена до операції диференціювання? (Інтегрування)

Молодці (саме таке слово отримали учні по вертикалі), теоретичний багаж

ваших знань з теми Інтеграл достатньо великий. Давайте тепер подивимось, як вивмієте застосовувати його на практиці.

2. Гра «Мікрофон»

Студентам пропонуються усно  елементарні функії для обчислення похідних та інтегралів

IV. Історичні відомості (студенти  першої групи)  (10 хв)

(Розповідь супроводиться презентацією)

Наука, що на сьогодні називається математичним аналізом, виникла в працях багатьох видатних математиків XVII століття - спочатку у вигляді окремих теорем та методів розв'язування деяких задач. До кінця XVII століття основні положення цієї нової для того часу науки остаточно оформилися (причому одночасно) в роботах двох найвизначніших учених тієї епохи - англійського фізика та математика Ньютона та німецького математика і філософа Лейбніца.

Виникнення цієї математичної дисципліни не випадково припадає саме на XVII століття. У цю епоху розвиток науки та техніки дійшов тієї межі, коли для подальшого просування вперед необхідно було глибше проникнути у суть речей, вивчити закони природи та процеси, що відбуваються в навколишньому середовищі.

Всі процеси протікають з певною швидкістю, всі величини, що беруть участь у цих процесах, змінюються, причому вони взаємозв'язані. Тому постала необхідність у такому апараті, за допомогою якого можна було б вивчати змінні процеси. Саме такий апарат і був розроблений у математичному аналізі. Таким чином, виникнення математичного аналізу було історично неминучим: цього вимагали потреби механіки, фізики та техніки. У свою чергу, саме ці вимоги були визначені рівнем розвитку виробничих сил суспільства. Проте повне його обґрунтування було дано лише наприкінці XIX століття.

Ключовими поняттями математичного аналізу є поняття функції, границі, похідної та інтеграла.

Термін „функція" вперше запропонував у 1692 р. видатний німецький філософ і математик Готфрід Вільгельм Лейбніц (1646-1716) для характеристики відношення відрізків, а перше означення функції, яке вже не було пов'язане з геометричними уявленнями, сформулював Йоган Бернуллі (1667-1748) у 1718 р. Уточнив це поняття Леонард Ейлер (1707-1783) і ввів символ функції f(x).

Похідна — одне з фундаменталь­них понять математики. Відкриттю похідної та основ диференціаль­ного числення передували роботи французьких математиків П'єра Ферма (1601—1665), який у 1629 р. запропонував способи знаходження найбільших і найменших значень функцій, проведення дотичних до довільних кривих, що фактично спиралися на застосування по­хідних, а також Рене Декарта (1596—1650), який розробив метод координат і основи ана­літичної геометрії. У 1670—1671 рр. англій­ський математик і механік Ісаак Ньютон (1643—1727) і дещо пізніше у 1673—1675 рр. німецький філософ і математик Готфрід Вільгельм Лейбніц (1646—1716) незалежно один від одного побудували теорію диферен­ціального числення. І.Ньютон прийшов до по­няття похідної, розв'язуючи задачі про миттє­ву швидкість, а Лейбніц — розглядаючи геомет­ричну задачу про проведення дотичної до кри­вої. Термін «похідна» ввів у 1797 р. французький математик Жозеф Луї Лагранж (1736—1813). Він ввів і сучасні позначення для похідної у вигляді та f^./. Ньютон, який у своїх підходах до обґрунтування математичного ана­лізу широко застосовував фізичні уявлення, похідну називав флюксією (дослівно з лати­ни — «витіканням»), а саму функцію флюентною (дослівно «текучістю»). Ці терміни Нью­тона не прижилися.

За допомогою диференціального числення було розв'язано багато задач теоретичної ме­ханіки, фізики та астрономії. Зокрема, викори­стовуючи методи диференціального числення, вчені передбачили повернення комети Галлея, що стало тріумфом науки XVIII ст.

Подібно тому, як Архімед відкривши закон важеля, сказав: «Дайте мені точку опори і я зрушу Землю», так і сучасники Ньютона казали: «Складіть нам диференціальне рівняння усіх рухів у природі і навчіть їх інтегрувати, тоді ми будемо подібні Богу, оскільки за допомогою обчислень точно будемо знати майбутні події». Д.О.Дравс

За допомогою цих методів математики у XVIII ст. вивчали властивості різних кривих, знайшли криву, по якій найшвидше падає ма­теріальна точка, навчилися знаходити криви­ну ліній.

І тепер поняття похідної широко застосо­вується у різних галузях науки та техніки.

Історія розвитку понять інтеграла й інтегрального обчислення пов’язана з потребою в обчисленні площ фігур, а також поверхонь і об’ємів довільних тіл. Передісторія інтегрального обчислення сягає глибокої давнини: ідеї інтегрального обчислення можна знайти в роботах давньогрецьких учених Евдокса Кнідського (бл.408-355 до н.е.) і Архімеда (бл.287-212 до н.е.).

Евдокс Кнідський (бл. 408-355 рр. до н. е.) - старогрецький вчений. Дав повний доказ теореми про обсяг піраміди; теореми про те, що площі двох кіл відносяться як квадрати їх радіусів. При доведенні він застосував так званий метод «вичерпання», який знайшов своє використання (з деякими змінами) у працях його послідовників. Через дві тисячі років метод «вичерпання» був перетворений у метод інтегрування, за допомогою якого вдалося об'єднати різні завдання - обчислення площі, об'єму, маси, роботи, тиску, електричного заряду, світлового потоку і багато, багато інших.

Задачу про знаходження площі сектора параболи розв’язав Архімед в III ст. до н.е.. Звичайно у Архімеда немає ще загального поняття інтеграла. Знак інтегралу вперше ввів Лейбніц у XVIII ст.

Давайте з'ясуємо, як саме ми можемо застосувати похідну і визначений інтеграл в фізиці.

V. Застосування похідної у фізиці ( доповідь групи “Похідна») (15 хв)

 Центральні поняття диференціального числення - похідна та диференціал. Операцію знаходження похідної називають диференціюванням.

Задача на знаходження миттєвої швидкості нерівномірного руху за відомою залежністю координати х від часу розв'язується так:

 похідною від координати є швидкість;

a(t)= ^/(t)=^:x^//(t) похідна від швидкості за часом є прискорення.

Таким чином, прискорення - друга похідна від координати за часом.

З точки зору фізики диференціювання - це визначення швидкості зміни змінної величини.  сила струму є величиною , яка є похідна по часу від заряду

потужність – величина, яка є похідною від роботи по часу.

Задача 1.

Тіло масою 2 кг рухається прямолінійно за законом x(t)=t ²+t+l. Координата вимірюється в метрах, час t - в секундах. Знайти:

а) діючу силу; б) кінетичну енергію тіла через 2 с після початку руху.

Розв’язання

 ;

при  t= 2c,  

 ; 

                                        

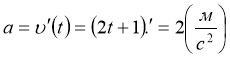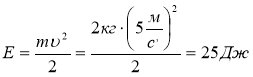
                                                Відповідь: 4 Н; 25 Дж

 

Задача 2.

Робота, що виконується при стисканні пружини на х см задається рівнянням:  A(x) = 230x + 2x³. Яка сила пружності виникає в пружині при її стисканні на 2 см?

Розв’язання

F(x) = A’(x);

F(x) = 230 + 6x²;

F(x) = 230 + 0,02² = 230,0024 (H).

Відповідь: 230,0024 (H).

 

Задача 3.

Заряд в провіднику опором 2 Ом змінюється з часом за законом
q(t) = 5t – 2t² + 4t³. Визначте напругу на кінцях провідника через 2 с після початку відліку часу.

Розв’язання

;

;

;

;

.

Відповідь: 90 В.

 

Задача 4.(самостійно розв’язати)

Знайдіть лінійну густину неоднорідного стержня довжиною 40 см, маса якого змінюється за законом m(l) = 2l² + 3l.

Розв’язання

;

кг/м.

Відповідь: 4,6 кг/м.

VI. Застосування інтегралу у фізиці. (15 хв)

За допомогою  визначеного інтегралу можна визначити

А =	Роботу при змінній силі
А =	Робота при змінній потужності
х =	Координата тіла
v =	Швидкість тіла
т =	Маса стержня
q (t) =	Електричний заряд
Q =	Кількість теплоти

А  тепер розглянемо окремо:

1. Обчислення шляху( координати тіла) х =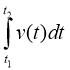

Задача 1. Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом v=2t+1(м/с). Знайти шлях, який пройде тіло за інтервал часу від t ₁ =1c, до  t₂ =3c.

Розв’язання

 

 

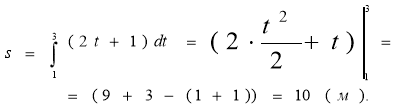
2. Обчислення роботи змінної сили       А =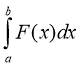                                              

Задача 2. Обчислити роботу, яку потрібно виконати, щоб відкачати воду із ями глибиною 4м, маючи квадратний переріз зі стороною  2м. Густина води ρ=10³ кг/м³ .

Розв’язання:  

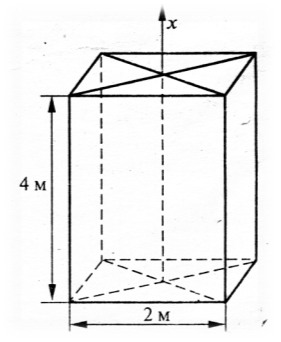
Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4 м², визначається вагою шару води, що знаходиться вище від цього перерізу. Отже

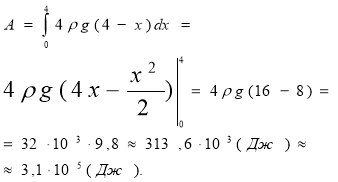
3. Знаходження маси стержня за його зміною густини

                                                     т =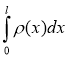

Задача 3. Знайти масу стержня довжиною 35см, якщо його лінійная густина змінюється по закону  ρ(l)=(4l+3)(кг/м)

Розв’язання:

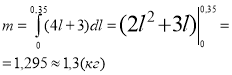
За означенням, сила струму є похідною від кількості електрики Q = Q(t), де t – час, тобто I(t) = Q’(t). А тоді функція Q = Q(t) є первісною для функції І = І(t), тому кількість електрики, що проходить через поперечний переріз провідника за час від t1 до t2, можна обчислити за формулою

 

Задача 4. Знайти кількість елетрики, що проходить через поперечний переріз провідника за 10с, якщо  сила струму змінюється за законом I(t)=(4t+1)(A)

Розв’язання

 

 

 

VII. Закріплення знань (до 15  хв)

Студентам пропонується

1. заповнити таблицю

№	Величини	Знаходження похідної	Знаходження інтеграла
1	S – переміщення v – швидкість a – прискорення
2	A – робота F – сила
3	q – електричний заряд I – сила струму
4	m – маса неоднорідного стержня  – лінійна густина стержня

 

Таблиця для самоперевірки

 

№	Величини	Знаходження похідної	Знаходження інтеграла
1	S – переміщення v – швидкість a – прискорення	v(t) = S’(t) a(t) = v’(t)
2	A – робота F – сила	F(x) = A’(x)
3	q – електричний заряд I – сила струму	I(t) = q’(t)
4	m – маса неоднорідного стержня  – лінійна густина стержня	(l) = m’(l)

 

2. розвязати задачі

 

Задачі для роботи в групах

Група «Історія»	Група «Похідна»	Група «Інтеграл»
Сила струму в провіднику змінюється за законом I(t) = 4 + 2t. Яка кількість електрики пройде через поперечний переріз провідника за час від другої до шостої секунди?	Знайдіть масу неоднорідного стержня довжиною 35 см, якщо його лінійна густина змінюється за законом (l) = 4l + 3.	Знайдіть кількість заряду , що протікає через поперечний переріз провідника за час від t=0  до t=п/2секунд, якщо сила струму  змінюється  за законом i= cost.

 

На розв’язання задач групам відводиться 10 хв.

 

VIII. Підведення підсумків заняття (3хв)

 

Скажіть, будь ласка, що саме ми з вами робили сьогодні на уроці?

(розв’язували задачі фізики, перекладали мовою математики проблеми, які стоять перед іншими науками.)

Секретарі груп здають листи оцінювання і виставляються оцінки за заняття.

IX. Рефлексія  (2 хв)

Вправа «Закінчи речення»

1. Ми сьогодні говорили…
2. Ми сьогодні виконували…
3. Ми сьогодні дізналися…
4. Найбільше зацікавило…

X. Домашнє завдання

Визначений інтеграл широко застосовується не тільки в математиці та фізиці, а й, наприклад, в хімії, біології та інших науках. Про такі застосування пропонуємо вам підготувати доповіді на наступние заняття.

Розв’язати задачі.

1. Тіло рухається уздовж осі  Ox за законом: x= 2t – 1/t. Знайти прискорення тіла в момент часу  t=2c/
2. Тіло масою 6кг рухається за законом:S_x= t²_- 3t+2. Знайдіть кінетичну енергію тіла за 10 секунд після початку руху.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток А

 

 

Лист оцінювання

П.І.П. студента

Кросворд (1 бал за правильну відповідь)

Підготовк проекту ( 0 – 5 балів)

Захист проекту (5-10 балів)

На протязі заняття (задача – 4 бали,  1 доповнення – 1 бал)

Результат  сам. роботи (0-5 балів)

Підсумки заняття (0-2 бали)

Сума балів

Оцінка

Сума балів команди

Оцінка

6

9

10

11

Бали

6-9

14-15

16-20

20 і ˃

 

 

 

Додаток Б

№	Величини	Знаходження похідної	Знаходження інтеграла
1	S – переміщення v – швидкість a – прискорення
2	A – робота F – сила
3	q – електричний заряд I – сила струму
4	m – маса неоднорідного стержня  – лінійна густина стержня

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток В

Задачі для роботи в групах

Група «Історія»	Група «Похідна»	Група «Інтеграл»
Сила струму в провіднику змінюється за законом I(t) = 4 + 2t. Яка кількість електрики пройде через поперечний переріз провідника за час від другої до шостої секунди?	Знайдіть масу неоднорідного стержня довжиною 35 см, якщо його лінійна густина змінюється за законом (l) = 4l + 3.	Знайдіть кількість заряду , що протікає через поперечний переріз провідника за час від t=0  до t=п/2секунд, якщо сила струму  змінюється  за законом i= cost.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток Г