Аналіз методик підготовки до ЗНО з математики

Зміст

Вступ ________________________________________________________ 3

1. Основні методики по підготовці до ЗНО з математики ­­­____________  4

1.1. Проблеми при підготовці до ЗНО ___________________________ 4

           1.2. Методична підготовка ____________________________________ 7

     1.3. Система роботи __________________________________________ 8

Висновок по розділу __­­­­­­­­­­­­­­­­­­­­­­­_________________________________________ 11

2. Психологічне забезпечення готовності школярів до здачі ЗНО _____ 12

    2.1. Психологічна складова успішної підготовки до ЗНО __________ 12

    2.2. Можливі психологічні труднощі ___________________________ 13

3. Система роботи школи та Зовнішнє незалежне оцінювання ________ 16

    3.1. Педагогічна складова ____________________________________ 16

    3.2. Розвиваюча складова ____________________________________ 18

4. Система роботи вчителя з підготовки учнів до успішної здачі ЗНО в сучасних умовах. (Практична частина) ______________________________ 19

    4.1. Методичні рекомендації для підготовки учнів до виконання завдань бланку А ________________________________________________ 19

    4.2. Методичні рекомендації для підготовки учнів до виконання завдань бланку Б _________________________________________________ 25

Висновок ____________________________________________________ 27

Література ___________________________________________________ 29

 

 

 

 

 

 

Вступ

Актуальність розробки методик підготовки учнів до ЗНО пов'язана з тим, що після введення в шкільну практику Зовнішнього незалежного оцінювання виникло безліч проблем, як у вчителів, так і в учнів. ЗНО в Україні почало формуватись з 2004 року, і з того часу вийшло немало різної допоміжної літератури про те, що необхідно робити вчителям щоб покращити підготовку учнів для успішної здачі тестування.

Чи можуть школярі успішно здати Зовнішнє оцінювання без відповідної, спеціальної підготовки? Як показує практика – здобувачі освіти в результаті зіштовхуються з численними труднощами, як з психологічної, так і з методичної точки зору. Для вирішення психологічних труднощів потрібна система занять спрямована на зняття емоційної напруженості при здачі іспиту в новій, не звичній для школярів формі. Частина проблем безпосередньо пов'язана з традиційною подачею матеріалу в шкільних підручниках. Учні не готові і не завжди вміють виконувати завдання в тестовій формі. Для вирішення цієї проблеми необхідно вирішувати завдання не тільки в вигляді тестів, а й приділяти велику увагу розв’язуванню задач різними способами. Розібрати, які помилки допускаються учнями при вирішенні тих чи інших типів завдань найчастіше. В першу чергу потрібно проаналізувати методики підготовки учнів до успішної здачі випускного іспиту з математики в рамках ЗНО.

Для вирішення завдань будуть використані наступні методи: вивчення літератури та опитування викладачів.

 

2. Основні методики по підготовці до ЗНО з математики

1.1 Проблеми при підготовці до ЗНО

Результати ЗНО виявили ряд невирішених проблем, характерних для підготовки різних категорій випускників. Це дозволяє висловити деякі загальні рекомендації, спрямовані на вдосконалення процесу викладання і підготовки учнів середньої школи.

1. Необхідно вдосконалювати методику формування базових умінь, що становлять основу математичної підготовки випускників середньої школи.
2. Аналіз результатів виконання базових завдань з курсу алгебри та початків аналізу показав наявність позитивної динаміки в оволодінні матеріалом розділу «Тригонометрія». В той же ж час викликають тривогу невисокі результати виконання завдань по розв’язуванню ірраціональних рівнянь та логарифмічних нерівностей. Слід звернути більшу увагу для засвоєння учнями стандартних алгоритмів розв'язання завдань такого типу.
3. Геометрична підготовка випускників школи продовжує залишатися невисокою, тому як і раніше необхідно посилити увагу вчителів до викладання курсу геометрії в основній і старшій школі, щоб в процесі навчання учні не тільки опановували теоретичними фактами курсу, а й набували вміння проводити обґрунтовані міркування при вирішенні геометричних задач і математично грамотно записувати отримане рішення.
4. Найнижчі результати учні показали при вирішенні завдань, які найважче піддаються алгоритмізації: завдання з геометрії, завдання прикладного змісту (де потрібно застосувати вміння читати графіки, вирішувати сюжетні завдання), а також завдання, для розв’язування яких потрібно застосувати елементарні навички дослідницької роботи.
5. Також слабкою залишається підготовка учнів з питань: виконання спільних дій над звичайними і десятковими дробами; перетворення многочленів; перетворення алгебраїчних дробів; перетворення виразів, що містять степінь з цілим показником; перетворення ірраціональних виразів; розв’язування квадратних, дробово-раціональних рівнянь і нерівностей; визначення властивостей функції за допомогою графіка;

Починаючи викладати математику з 5 класу, у вчителя з'являється можливість, починати готувати школярів до ЗНО задовго до його початку. А саме посилено працювати над повторенням матеріалу і систематизацією знань, використовувати в процесі навчання різні види діяльності і нові форми контролю. Все це готує здобувачів освіти до іспиту як психологічно, так і дозволяє підвищити якість математичної освіти.

Щоб добре підготувати учнів до ЗНО, вчителю потрібно самому багато і постійно навчатися, удосконалювати свою майстерність, і поряд з традиційними підходами використовувати інноваційні технології та ресурси мережі Інтернет.

Школа сьогодні стрімко змінюється, намагається іти в ногу з часом. Важливо не стільки дати дитині якомога більший багаж знань, скільки забезпечити її загальнокультурний, особистісний і пізнавальний розвиток.

Серед різноманітних напрямків нових педагогічних технологій для досягнення поставленої мети вчителеві рекомендується використовувати в своїх методиках такі засоби:

• Навчання в співробітництві
• Метод проектів
• Індивідуальні консультації
• Робота в малих групах і парах
• Використання ІКТ

 

Навчання в співробітництві

Ідея проста - клас розбивається на невеликі групи, в кожній з яких є сильний учень. Кожна команда отримує загальне завдання і працює над ним до тих пір, поки всі члени групи повністю не зрозуміють і не виконають дану роботу.

Метод проектів

На сучасному етапі розвитку освіти проектна методика широко поширена. Цей метод можна використовувати для накопичення теоретичних даних і для відпрацювання навичок вирішення завдань по кожній темі. Тобто учні створюють для себе міні-проекти у вигляді карток для покрокового вирішення завдання.

В організації роботи за проектом виділяються наступні етапи:

1. Підготовчий

Підготовчий етап проходить в стислій формі. Учитель біля пояснює чергове завдання, акцентуючи увагу учнів на основні формули, закони, властивості та визначення.

2. Основний

Основний етап це робота в групах над створенням карток для всіх завдань. Триває протягом першого півріччя 10 класу, а в 11 класі доповнюється в міру проходження нових тем.

3. Кінцевий

Кожним здобувачем освіти створюється індивідуальна папка «Моя підготовка до ЗНО», що містить необхідні теоретичні відомості і набір вирішених завдань по кожній темі, ця папка допомагає при самостійній роботі вдома. Захисту проекту немає, але в міру відпрацювання кожної теми задається залік на знання формул, законів, властивостей і визначень.

Роботу над цими міні-проектами можна проводити в позаурочний час на факультативі.

 

 

 

Індивідуальні консультації

Консультації по необхідності можна проводити в індивідуальному порядку.

Роботу в малих групах і парах

Цей прийом є частиною навчання у співпраці, і так само використовується для формування груп за рівнем знань з метою організації диференціального навчання.

Використання ІКТ

• Дозволяє оптимізувати процес навчання
• Підвищує мотивацію учнів
• Сприяє підвищенню якості знань
• Дозволяє учням краще зрозуміти матеріал
• Забезпечує високий темп проведення уроку і т. д.

       

      1.2. Методична підготовка

Багато вчителів, репетитори та батьків, які допомагають своїм дітям підготуватися до ЗНО, намагаються перерішувати якомога більше варіантів попередніх років. Такий шлях неперспективний. По-перше, варіанти не повторюються. По-друге, у школяра не формується стійкий загальний спосіб діяльності із завданнями відповідних видів. По-третє, у школяра з'являється почуття розгубленості і повної безнадійності: завдань так багато і всі вони такі різні. Запам'ятати рішення всіх завдань неможливо. Тому набагато розумніше вчити школярів загальним універсальним прийомам та підходам для розв’язування завдань.

Таким чином, підготовка не зводиться до «натаскування» випускника на виконання певного типу завдань, що містяться в демонстраційній версії іспиту. Підготовка до ЗНО означає вивчення програмного матеріалу з включенням завдань у формах, що використовуються при підсумковій атестації. Крім того, на початку першого семестру необхідно виявити сильні і слабкі сторони в знаннях учнів, на підставі цього створити цільові групи і сформулювати основні принципи побудови методичної підготовки до іспиту.

 

1.3. Система роботи

Можна запропонувати наступну систему роботи при підготовці школярів до здачі ЗНО з математики.

На початку навчального року випускники та їх батьки (обов'язково) знайомляться з планом підготовки до ЗНО та з додатковими матеріалами:

• зі структурою Зовнішнього незалежного оцінювання з математики;
• з переліком ресурсів мережі Інтернет
• зі списком посібників для підготовки до ЗНО
• з вимогами до рівня підготовленості учнів
• з порадами психологів

 

Вивчення програмного матеріалу дозволяє організувати підготовку до ЗНО вже з початку навчального року 11 класу.

В основу покладені наступні концептуальні положення:

• Особистісний підхід, педагогіка успіху, педагогіка співпраці. Включає два принципи:

- активне навчання (учні повинні зрозуміти, що для засвоєння наукових істин одної старанності недостатньо, а потрібні довгі часи кропіткої роботи);

- диференційоване навчання та оцінки.

Цей принцип реалізується досить просто. Пропонуються завдання різної складності - від типових до важких. І кожен учень може вибирати для розв’язування ті завдання, які йому доступні.

• Навчати математиці означає навчати розв'язанню задач, а навчати розв'язанню задач означає навчати вмінням розв'язати типові задачі
• Індивідуалізувати навчання "важких" і "обдарованих" (цільові групи).
• Органічний зв'язок індивідуальної та колективної діяльності (Робота в групах та індивідуально).

Характерною особливістю нашого часу є прагнення багатьох вчителів перебудувати навчальний процес, активізувати учнів, зацікавити їх, привчити до самостійної роботи (комп'ютерне тестування, аналіз вирішених завдань, критерії оцінювання тощо).

З урахуванням першого принципу всі пропоновані завдання розбиті за наступними темами:

• Перетворення виразів.
• Рівняння і нерівності.
• Розв'язання задачі.
• Системи рівнянь і нерівностей.
• Відсоток. Прогресія. Пропорція.
• Функція.
• Похідна і первісна.
• Геометричні завдання (розглядаються на уроках геометрії).

Відповідно до даних тем і сильних сторін учнів можна розплановувати подальшу роботу.

 

Геометрія

При викладанні геометрії необхідно приділяти увагу формуванню базових знань курсу стереометрії. (Кут між прямими в просторі, кут між прямою і площиною, кут між площинами, багатогранники і т.д.). Разом із цим необхідно знаходити можливість відновлювати базові знання курсу планіметрії (прямокутний трикутник, розв’язування трикутників, чотирикутники і т.д.). При вивченні геометрії необхідно:

• поліпшувати наочність викладання;
• більше приділяти уваги питанням зображення геометричних фігур;
• формувати конструктивні уміння та навички;
• застосувати геометричні знання для вирішення практичних завдань.

 

Досить часто вчителі застосовують такі види роботи:

Клас умовно ділиться на три групи. Для себе ці групи можна назвати А, В, С.

• Група С - учні, які цікавляться предметом, розв’язують завдання
• підвищеного рівня.
• Група В - самостійно можуть вирішувати завдання середнього рівня.
• Група А - учні, які вирішують стандартні завдання, використовуючи зразки і алгоритми рішення.

Завдання для кожної групи різні. При організації тематичної підготовки до іспиту можна використовувати таку форму як довгострокове домашнє завдання. Учням пропонується набір завдань, які вони повинні виконати під час вивчення конкретної теми.

Довгострокові домашні завдання виконуються в спеціальних зошитах, які потім здають на перевірку. Після перевірки, рекомендується виконати роботу над помилками.

Цю форму роботи рекомендується використовувати, так як для успішної здачі ЗНО недостатньо добре працювати на уроках і регулярно виконувати домашні завдання, необхідно ще додаткова підготовка. Довгостроковими домашніми роботами, вчитель певним чином зобов'язує учнів займатися додатково.

Особливу увагу в процесі діяльності з підготовки учнів до ЗНО займає моніторинг якості навченості, який повинен бути системним і комплексним. У зв'язку з цим на кожного учня заводиться діагностична карта, куди протягом двох років вносяться результати діагностичних, самостійних, контрольних робіт. Це дозволяє простежити ступінь підготовки учня з тієї чи іншої теми і контролювати відпрацювання навичок, готувати індивідуальні завдання, диференційовано підходити до планування уроку. Всі тренувальні тести, виконані на листочках або на бланках ЗНО, учні збирають в папки, які зберігаються в кабінеті математики. Збираючи тренувальні тести, вчитель може відстежувати динаміку зростання в окремих учнів, контролювати виконання роботи над помилками, виявляти теми, які на даному етапі навчання погано засвоєні, для коригування процесу навчання через повторення, використовувати для організації індивідуальної роботи.

 

Тест на відповідність

Це ще одна необхідна форму контролю на етапі підготовки до ЗНО. Основна складність в підготовці до іспиту учнів з низьким рівнем успішності полягає в тому, щоб домогтися своєчасного вивчення ними формул, визначень, алгоритмів вирішення базових завдань.

Залік - найбільш ефективна форма контролю знань учнів. Протягом усього періоду підготовки до ЗНО проводяться тематичні заліки, міні-заліки. Як правило, залікова картка містить теоретичні та практичні завдання різного рівня: базового та підвищеного, що дозволяє підтримувати теоретичні знання на високому рівні та підвищити результативність підготовки до іспиту. Перед заліком проводяться тренувальні тестування.

Висновок по розділу

Проведення уроків різнорівневого узагальнюючого повторення дозволяє здійснити диференційований підхід і систематизацію матеріалу до найбільш проблемних завдань діагностичної роботи, і при цьому провести своєчасну ліквідацію прогалин в знаннях учнів.

Як показала практика, застосування описаних вище способів, прийомів, методів, технологій в роботі з учнями, в ході підготовки до іспитів, дозволило забезпечити отримання ними досить непоганих навиків, і успішної здачі ЗНО в минулому навчальному році.

2. Психологічне забезпечення готовності школярів до здачі ЗНО

2.1 Психологічна складова успішної підготовки до ЗНО

Для того щоб краще зрозуміти, що являє собою єдиний державний іспит з психологічної точки зору, порівняємо його з традиційним іспитом. ЗНО кардинально відрізняється як від усного іспиту, так і від традиційного письмового.

Відмінні риси	Традиційний іспит (усний або письмовий)	ЗНО
Що оцінюється?	Оцінюються не просто фактичні знання, а вміння їх піднести. Рівень розвитку усного мовлення може дозволити "приховати" прогалини в знаннях.	Оцінюються фактичні знання і вміння міркувати, вирішувати, а також вміння утримуватися в рамках завдання, розуміти формулювання.
Що впливає на оцінку?	Великий вплив роблять суб'єктивні фактори: контакт з екзаменатором, загальне враження і т.д	Оцінка максимально об'єктивна, так як виключений особистісний фактор.
Можливість виправити власну помилку	На усному іспиті легше помітити помилку за рахунок зворотного зв'язку від екзаменатора і можна її виправити під час розповіді або при відповіді на питання екзаменатора, на письмовому – при перевірці власної роботи	Можна помітити і виправити помилки при самоперевірці.
Хто оцінює?	Знайомі учневі люди.	Комп'ютер, незнайомі і невидимі експерти.
Коли можна дізнатися результати іспиту?	На усному іспиті – практично відразу, на письмовому – протягом декількох днів.	Протягом декількох тижнів
Зміст іспиту.	Учень повинен продемонструвати володіння певним фрагментом навчального матеріалу (певною темою, питанням і т.д.)	Іспит охоплює практично весь обсяг навчального матеріалу.

 

Крім когнітивної складової, випускний іспит має також особливий психологічний сенс. Психологічно період завершення навчання в школі представляє особливу складність для учнів тому, що це час першого дорослого випробування, яке показує, наскільки випускники підготовлені для дорослого, самостійного життя. Тому результати випускних іспитів мають для учнів особливе значення.

Можна виділити деякі найбільш значущі психологічні характеристики, які потрібні в процесі складання ЗНО:

• Висока мобільність.
• Чіткість і структурованість мислення.
• Високий рівень організації діяльності.
• Сформованість внутрішнього плану дій.
• Висока і стійка працездатність.
• Високий рівень концентрації уваги.

Таким чином, процедура проходження Зовнішнього незалежного оцінювання – справа не легка. Вона відрізняється від звичного досвіду учнів і пред'являє особливі вимоги до рівня розвитку психічних функцій.

 

2.2 Можливі психологічні труднощі

ЗНО має ряд особливостей, які можуть викликати у випускників певні труднощі. Розділимо їх на кілька груп, в залежності від того, з чим вони пов'язані, коротко їх охарактеризуємо і намітимо основні шляхи попередження.

Когнітивні труднощі.

Це труднощі, пов'язані з особливостями переробки інформації, зі специфікою роботи з тестовими завданнями. Не будемо зупинятися на змістовній проблемі – який обсяг знань засвоєний конкретним учнем і наскільки він упорядкований, – це більшою мірою педагогічна проблема. Припустимо, що учень в достатньому обсязі володіє навчальним матеріалом.

Перш за все, значні труднощі може представляти сама робота з тестовими завданнями. Хоча в даний час метод тестування все ширше застосовується для перевірки знань учнів, але реальність шкільної практики не встигає за змінами. У більшості випадків навчання проводиться традиційними методами. Разом з тим тестування передбачає формування особливих навичок: вміння виділяти суттєві сторони в кожному питанні і відокремлювати їх від другорядних, вміння оперувати фактами і положеннями, вирваними із загального контексту. Традиційне навчання на цьому, як правило, не загострює увагу. Навпаки, акцент робиться на зв'язності викладу, умінні вибудовувати взаємозв'язки в рамках окремої теми.

Для подолання когнітивних труднощів необхідно рухатися в двох напрямках: освоювати навички роботи з тестами та допомагати випускнику виробляти індивідуальну стратегію діяльності. І якщо навички роботи – це більшою мірою педагогічна задача, то вироблення індивідуальної стратегії – це завдання психологічне.

Особистісні труднощі.

Ці труднощі обумовлені особливостями сприйняття учнем ситуації іспиту, його суб'єктивними реакціями і станом.

Перш за все стресовою є сама ситуація. На іспиті учень повинен за обмежену кількість часу продемонструвати свої знання з певного питання або впоратися із запропонованими завданнями, причому результати цієї діяльності будуть оцінюватися. На іспиті учень показує, чого він насправді навчився, які в дійсності його знання. Традиційно в нашій шкільній системі іспити наділяються особливою значимістю, а успішність або неуспішність учня при здачі іспиту активно обговорюється батьками і педагогами. Іспит - це не просто рядова перевірка знань, це кульмінаційний момент, готуватися до якого починаються заздалегідь. Стрес на іспиті появляється через те, що ця процедура пов'язана з самооцінкою підлітка: наскільки я дійсно розумний, наскільки можу впоратися із запропонованими мені завданнями? Дефіцит часу значно підвищує тривогу учня, у нього з'являється страх «не встигнути».

Традиційно ситуація іспиту в школі багато в чому пом'якшується тим, що учнів оточують знайомі люди. Незалежно від того, як вчителі ставляться до підлітка, їх поведінка передбачувана, що багато в чому сприяє зниженню тривоги, яку відчуває учень.

При здачі ЗНО випускники позбавлені такої підтримки. Там все чуже-люди, учні, приміщення. Приймають і оцінюють результати іспиту незнайомі люди, що призводить до підвищення тривоги і недостатньої сконцентрованості на завданні.

Висновок до розділу

Підводячи підсумки, слід відзначити, що основний наслідок особистісних труднощів – це підвищений рівень тривоги, невпевненості учнів на іспиті, що призводить до дезорганізації їх діяльності, зниження концентрації уваги і працездатності. Тривога - це дуже енергоємне заняття. Чим більше дитина тривожиться, тим менше сил у неї залишається на навчальну діяльність. Тому подолання особистісних труднощів, перш за все, має бути спрямоване на зниження тривоги.

Тому психологічна підготовка до ЗНО необхідна. Для того щоб забезпечити повноцінну психологічну підготовку, дуже важливо об'єднати сили випускників, педагогів, батьків.

3. Система роботи школи та Зовнішнє незалежне оцінювання

3.1. Педагогічна складова

Шкільна математична освіта повинна бути спрямована в першу чергу на розвиток розумових здібностей школярів. Математика покликана вчити школярів вмінню міркувати і доводити, наводити приклади та контрприклади, використовувати методи індукції, дедукції, узагальнення та конкретизації і т.д. – всьому тому, без чого неможливий науково-технічний прогрес і без чого неможливо продовження освіти і отримання сучасних професій. При вирішенні цих найважливіших дидактичних проблем здійснюється підготовка учнів до здачі Зовнішнього незалежного оцінювання. Підготовка учнів до ЗНО – це один з нових інструментів формування не тільки математичної культури, а й забезпечення конкурентоспроможності учня.

Випускник школи повинен бути готовим:

Вивчати:

• власний і чужий досвід і отримувати користь з них;
• прийоми навчання, систематизувати і організовувати їх;
• методи постановки і вирішення проблем;
• методи самоорганізації та самоосвіти.

Шукати:

• необхідну інформацію в різних базах даних;
• необхідну інформацію, опитуючи оточуючих (товаришів, вчителів, фахівців);
• відповіді на важкі питання у експертів;
• прийоми і методи класифікації інформації.

Співпрацювати, тобто:

• вміти працювати в групах;
• вміти приймати розв’язок;
• вміти залагоджувати розбіжності і конфлікти;
• вміти домовлятися;
• вміти розробляти і виконувати договори.

Форми роботи з учнями старшої школи по математиці мають головні відмінності:

1. У старшокласників вже є стійкі інтереси до предметів і усвідомлені пріоритети. А значить, вибирати зміст, навіть способи його вивчення, рівень складності завдань необхідно з урахуванням запитів учнів. (Скажімо, в одному класі теорему Вієта для кубічного чотирьохчлена слід вивчати, а в іншому можна навіть і не згадувати.)

2. Підготовка повинна бути більш індивідуальною. У кожному класі стільки особистостей, скільки числиться учнів за списком. І кожна особистість зі своїми запитами і з обраним напрямком подальшої освіти, тому важливо враховувати запити кожного.

 

Відзначимо ще раз, що підготовка учнів до ЗНО не повинна бути самоціллю вчителя при роботі з одинадцятикласниками і, тим більше, не повинна зводитися тільки до неї. Вчити міркувати і доводити, правильно застосовувати необхідні і достатні умови, вчити індукції і дедукції, аналізу і синтезу, узагальненню і конкретизації, вмінню будувати приклади і приводити контрприклади, розвивати грамотну математичну мову, вивчати яскраві факти з історії математики і життя математиків, навчати дослідницькому підходу, самостійної дослідницької діяльності – як були, так і залишаються основними завданнями вивчення математики в старшій школі.

Коли учні добиваються хороших результатів у вивченні математики, то на роботу будь-який вчитель йде до своїх вихованців з радістю. Природним продовженням уроку стає спільне обговорення багатьох завдань, складання нових, а самим радісним і приємним стає не оцінка, а сам процес пізнання математики.

 

3.2 Розвиваюча складова

Процес пізнання і розвитку в школі не може обмежуватися рамками уроків, оскільки сама програма з шкільних предметів – мінімум з усього багатства світової науки і культури. Щоб найбільш ефективно сприяти розвитку здібностей і схильностей, врахувати особливості характеру і темпераменту, допомогти учням зорієнтуватися у виборі професії, розвинути психологічну основу для успішного навчання і продовження освіти, необхідні, по-перше, кваліфікована робота шкільного психолога; по-друге, продумана і налагоджена система позакласної роботи.

В даний час в різних школах дуже різноманітно будують позакласну роботу зі школярами. У деяких школах основний напрям відводиться на цікаве проведення дозвілля: художня самодіяльність, дискотеки, бальні танці, драматичні гуртки і т.д. в інших школах добре поставлена фізкультурно-оздоровча робота, військово-патріотичне виховання школярів. Є школи, де позакласна робота будується, в основному, на трудових справах, освоюванні основ конкретних професій.

Зупинимося на описі системи позакласної роботи школи, яка відводить першочергове завдання розвитку наукового світогляду школярів і більш глибокої підготовки учнів до подальшого навчання у вузах. Основна форма занять при цьому – предметні гуртки, олімпіади, творчі конкурси, інтелектуальні ігри, літні предметні табори, дистанційне навчання та дослідницька робота школярів.

4. Система роботи вчителя з підготовки учнів до успішної здачі ЗНО в сучасних умовах. (Практична частина)

4.1 Методичні рекомендації для підготовки учнів до виконання завдань бланку А

 

З введенням нової процедури атестації та проведення конкурсного іспиту до вузу перед учителем старших класів стоїть важливе завдання підготовки учнів до здачі ЗНО. При цьому їх потрібно не «натаскувати», а як вже говорилося навчити мислити, працювати самостійно.

Розглянемо деякі вправи, які потрібно опрацювати з учнями для успішної здачі ЗНО, так як таким завданням і методам їх розв’язання не завжди представлена достатня увага в сучасних підручниках для старшої школи.

 

Завдання 1. Спростити вираз .

1) 1; 2) 19; 3) 1; 4) 19.

Розв’язок. Крім традиційного способу – застосування основних тригонометричних тотожностей, для розв’язування даного завдання можливий і інший підхід.

Зауважимо, що жодна з відповідей не залежить від х, тому в початковий вираз замість х підставимо будь-яке «зручне» число. Нехай, наприклад, х=0. Тоді, підставляючи в початковий вираз, отримаємо:

Завдання розв’язане: тільки одна відповідь збігається з 1, тому вона і є правильною. Вірна відповідь - перша.

Завдання 2. Спростити вираз

1) ; 2) ; 3) ; 4) .

Перший спосіб. Нехай а=32 (2⁵), тоді значення виразу дорівнює . Тільки при підстановці в перший варіант відповіді а=32 ми отримаємо відповідь .

Другий спосіб. Позначивши . Тоді . Теперь 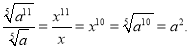Отже, вірна відповідь - перша

Завдання 3. Обчислити якщо

1) ;  2) -1;  3) 4;  4) .

Перший спосіб. Із умови знаходимо, що . Тоді

Другий спосіб Вірна відповідь - друга.

 

Завдання 4. Знайдіть всі корені рівняння

1) 2) 3) 4)

Перший розв’язок. Зауважимо, що та можна виразити через Отже, рівняння зводиться до найпростішого відносно. А якщо це так, то найбільш вірогідною є третя відповідь.

Другий розв’язок. Оскільки у всіх відповідях , то припустимо, що n=0. відповіді приймуть вигляд: 0; 0. Перша і четверта відпадають, оскільки при цих значеннях рівняння не визначено, а друга відповідь легко усувається перевіркою (ліва частина є ірраціональним числом, а права – раціональним). Вірна відповідь - третя.

Завдання 5. Вкажіть первісну функції .

1) ; 2) 3) 4)

Розв’язок. Це завдання простіше вирішувати диференціюючи функції, дані у відповідях. При диференціюванні не відбувається подвоєння аргументу, тому 1 і 3 відповіді відпадають. Четверта відповідь відпадає, оскільки похідна не збігається з. Залишається єдина відповідь - друга.

 

Розглянувши ці завдання можна зробити наступні висновки:

Дані розв’язки доступні для більшості учнів, тому стає очевидною необхідність і доцільність продумувати систему вправ, націлену на підготовку до успішного виконання подібних завдань всіма школярами. Відзначимо також, що ця робота не повинна здійснюватися тільки в 10-11 класах, як це робиться тепер через те, що змінилася система атестації. Необхідно починати з 7 класу. Скажімо, добре знання і застосування властивостей лінійної функції повинна забезпечувати програма 7 класу, а властивості квадратичної функції – програма 8 класу і т. д.

Наведемо приклади деяких вправ з різними способами розв’язування, які можна використовувати при роботі з учнями для підготовки до ЗНО.

Проведемо аналіз завдань за змістовно-методичними лініями.

Вирази і перетворення. У зв'язку з тим, що вирази і перетворення використовуються при вирішенні багатьох типів завдань, зупинимося тільки на декількох.

Завдання. Спростити вираз .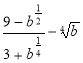

1) ; 2) 3; 3) 0; 4) .

Перший розв’язок. Послідовно перетворюємо:

.

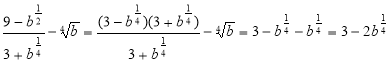Правильною є перша відповідь.

Другий розв’язок.  Нехай Тоді і вираз набуде вигляду

Третій розв’язок. Позначимо вихідний вираз через F (b).

1. Обчислимо значення виразу при b=1:

 

2. Відразу видно, що відповіді 2 і 3 не можуть бути вірними.

3. Тепер обчислимо значення першої та четвертої відповідей при b=1:

та

Звідси випливає, що правильною є перша відповідь.

Коментар.

Перше розв’язком зазвичай користуються школярі, які твердо засвоїли програму і вміють контролювати свої дії. Він аналогічний рішенню, яке виконують учні при написанні письмової контрольної роботи після вивчення теми. Якщо завдання буде дещо ускладнено (збільшено число елементів і їх різноманітність), то час виконання може серйозно зрости. Для реалізації такого розв’язку потрібно тверде знання формул скороченого множення і хороші навички виконання перетворень.

Другий розв’язок можна рекомендувати тим школярам, які допускають обчислювальні помилки і не завжди бачать «потрібні» формули. При збільшенні складності час виконання зросте незначно. Реалізація такого розв’язку передбачає вміння побачити потрібну заміну і використати відповідну формулу.

Третій розв’язок істотно відрізняється від перших двох. Він реалізується з урахуванням наступного міркування: якщо при якомусь допустимому значенні змінної значення вихідного виразу і відповіді відрізняються, то ця відповідь не є правильним. Звідси випливає, що якщо при якомусь значенні змінної всі значення відповідей, крім однієї, відрізняються від значення вихідного виразу, то правильним і буде та відповідь, значення якої дорівнює значенню вихідного виразу.

З приводу такого розв’язку можна висловити наступні міркування:

1. Це не зовсім математичне рішення, але в разі правильних обчислень, за правилами перевірки та оцінювання ЗНО, воно призведе до позитивної оцінки.

2. Після спеціальної підготовки (до прийняття рішень в певних умовах) такий розв’язок стає доцільнішим, тому що його реалізація призводить до серйозної економії часу.

 

Функції та їх властивості

Практично у всіх частинах ЗНО зустрічаються завдання, пов'язані з перевіркою властивостей функцій. Зрозуміло, що складність цих завдань дуже різна. Але сам факт включення завдань з функціями в різні розділи говорить про те, що вони є однією з найважливіших частин шкільної програми з математики. Отже підготовці до виконання завдань, пов'язаних з функціями, потрібно приділити особливу увагу. Розглянемо типове завдання, яке можна використовувати для підготовки до здачі ЗНО.

 

Завдання. Знайти найменше значення функції

Перший розв’язок. Так як функція може набувати лише невід’ємних значень, то змінні у та приймають найменші значення при одних і тих же значеннях змінної х. Знайдемо х, при якому приймає найменше значення: , де та . Так як та приймають найменше значення при х=0, то приймає найменше значення при х=0. Отже .

Відповідь: 2.

 Другий розв’язок. Відомо, що якщо a≥0, b≥0, то . При цьому рівність можна отримати лише в тому і тільки в тому випадку, якщо . Тоді . У нашому випадку рівність досягається тільки при х=0. В такому випадку функція приймає найменше значення. Звідси отримуємо, що найменше значення вихідної функції дорівнює 2 і досягається воно при х=0.

Третій розвязок. Перепишемо формулювання, яке задає функцію наступним чином: 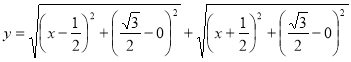. У декартовій системі координат розглянемо точки .

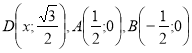Тоді 1)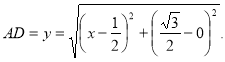

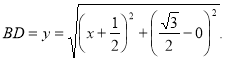
2) Точка D розташована на прямій .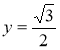

 

З) значення вихідної функції дорівнює сумі відстаней AD+BD.

В такому випадку все зводиться до вирішення відомої геометричної задачі: на прямій СD знайти таку точку D, щоб сума відстаней АD+ВD була найменшою.

Четвертий розв’язок. Для визначення найменшого значення застосуємо похідну:.

 

Знайдемо критичні точки: .

Розв’язуючи дане рівняння, отримуємо, що х=0. Дослідивши значення похідної, приходимо до висновку, що в цій критичній точці і є найменше значення функції.

Видно, що стандартне дослідження поведінки даної функції за допомогою похідної – досить складний процес. Тому підготовка учнів до ЗНО повинна передбачати навчання пошуку найбільшого і найменшого значень і без похідних (це повинно розглядатися в 8-10 класах).

 

4.2 Методичні рекомендації для підготовки учнів до виконання завдань бланку Б

 

Друга частина істотно відрізняється від першої. Основна відмінність полягає в наступному.

1. Пропонується завдання без варіантів відповіді. У кожному завданні слід її знайти і записати.

2. Завдання даної частини більш складні. Складність завдань пов'язана з тим, що розв’язок кожної задачі це, як правило, рішення двох - трьох стандартних завдань, об'єднаних одним формулюванням. Наприклад, пропонується не просто вирішити тригонометричне рівняння, а потрібно знайти кількість коренів на заданому відрізку (або їх суму).

З. Не всі завдання цієї частини рівноцінні. Але при їх виконанні не потрібно оформляти розв’язок і обґрунтовувати хід розв’язок, досить дати вірну відповідь.

4. При виконанні завдань другої частини можна використовувати будь-які факти, навіть маловідомі в шкільній практиці, сміливо користуватися ними для економії часу, не ризикуючи при цьому абсолютно нічим.

Наведемо факти, що дозволяють економити час виконання завдань другої частини.

1. Підібрати корінь многочлена F(х) і розділити многочлен на різницю отримавши його розкладання.

2. Знати і вміти застосовувати формулу складних відсотків.

3. Вміти вирішувати досить складну за формулюванням задачу графічно. При цьому допускаються готові шаблони. Наприклад, побудова графіка функції починати з побудови вертикальної і горизонтальної асимптот ( і відповідно).

4. Використовувати будь-які відомі формули, а не тільки ті, які представлені в підручнику.

 

Висновок

 

Щоб найбільш ефективно сприяти розвитку здібностей і схильностей, врахувати особливості характеру і темпераменту, допомогти учням зорієнтуватися у виборі професії, розвинути психологічну основу для успішного навчання і продовження освіти, необхідні:

по-перше, кваліфікована робота всього шкільного колективу, включаючи психолога;

по-друге, продумана і налагоджена система позакласної роботи.

З урахуванням цього були зроблені висновки про те, що робота вчителя не провинна зводитись лише на підготовку учнів до ЗНО. Вчити міркувати і доводити, правильно застосовувати необхідні і достатні умови, вчити індукції і дедукції, аналізу і синтезу, узагальненню і конкретизації, вмінню будувати приклади і будувати контрприклади, розвивати грамотну математичну мову, вивчати яскраві факти з історії математики і життя математиків, навчати дослідницькому підходу, самостійної дослідницької діяльності – як були, так і залишаються основними завданнями вивчення математики в старшій школі.

Якісна підготовка до ЗНО вимагає особливого повторення не тільки в 11 класі. Склад методичних засобів, підготовлених для навчання загальним методам, повинен включати такі компоненти:

• приклади завдань, які вирішуються цим методом;
• система вправ на засвоєння даного методу (для кожного класу, починаючи з 7-го, а в деяких завданнях і з 5-го);
• різні способи аналізу умов завдання, що приводять до правильного розв’язку;
• засоби самоконтролю діяльності з реалізації даного методу;
• евристики, що дозволяють визначити доцільність застосування методу;
• способи складання завдань, які можна вирішити вивченим методом.

Робота по підготовці до ЗНО буде ефективною, якщо в систему роботи школи і кожного класу окремо буде включено проведення, як мінімум, один раз на місяць тренінгів з подальшим якісним аналізом виконуваних робіт. Однак аналіз робіт учнів не повинен зводитися до виставлення балів і показу правильного розв’язку – він повинен включати всі можливі способи рішень кожного завдання і порівняння цих способів з урахуванням їх ефективності, естетики і тимчасових витрат. Особливо слід при цьому продумувати ті варіанти рішень, які не були реалізовані школярем, і розповісти їм про втрачені можливості.

 

 

Список літератури

 

1. Абдулханова-Славська К.А. Особистісні типи мислення // когнітивна психологія. М.: Наука. – 1986.
2. Айзенберг М.І. Навчання учнів методам самостійної роботи з підручником // Математика в школі. №6. – 1982.
3. Арутюнян Є.Б., Глазков Ю. А., Левітас Г. Г. Взаємне навчання школярів на уроках математики // Математика в школі. №4. – 1988.
4. Богоявленський Д. Н. Прийоми розумової діяльності та їх формування у школярів // Питання психології. №2. – 1969.
5. Гібш і.А. Розвиток мовлення в процесі вивчення шкільного курсу математики // Математика в школі. №6. – 1995.
6. Гузєєв В.В. Технологія проблемного семінару: синтез «мозкового штурму» і «творчої дискусії» // шкільні технології. №1. – 1998.
7. Гусєв В. А. та ін Позакласна робота з математики. - М.: Просвітництво. – 1977.
8. Дружинін В. Н. когнітивні здібності. Структура. Діагностика. Розвиток. М. – СПб: Per Se, Иматон. – 2010.
9. Л.О. Денищева, Ю. А. Глазков, К. А. Краснянська. Математика: збірник завдань. М.: Просвіта-2005.
10. Л.О. Денищева, Ю. А. Глазков, К. А. Краснянська та ін. Методика підготовки: книга для вчителя. М.: Просвіта-2005.
11. Зенкевич І. Г. естетика уроку математики. М.: Просвітництво-1981.
12. Колягін Ю.М., Ткачова М.И., Федорова Н. є. профільна диференціація навчання математики // Математика в школі. №4. – 1990.
13. Манвелов С. Г. завдання на розвиток самоконтролю учнів. М.: Просвітництво. – 1997.
14. Методика викладання математики в середній школі. Загальна методика / Упоряд. Р. С. Черкасов, А.А. Столяр. М.: Просвітництво. – 1985.
15. Смишляєв В. К. Практикум з вирішення завдань шкільної математики. М.: Просвітництво. – 1978.
16. Рижик В. І. 30000 уроків математики. М.: Просвітництво. – 2010.
17. Тализіна Н. Ф. управління процесом засвоєння знань. М.: Педагогіка. – 1975.