урок "Застосування інтеграла для обчислення площ плоских фігур"
11 клас
Тема. Застосування інтеграла для обчислення площ плоских фігур.
Мета уроку : узагальнення знань про інтеграли; навчитись обчислювати площу плоских фігур за допомогою інтеграла, за допомогою програми Gran1 навчитись будувати графіки, обчислювати інтеграли.
Хід уроку
І. Організаційний момент.
ІІ. Актуалізація опорних знань.
-Пригадаймо, який геометричний зміст інтеграла?(За допомогою інтеграла ми обчислюємо площу фігури, обмеженої контуром.)
-Запишіть формулу Ньютона-Лейбінца: 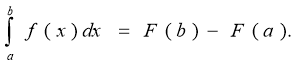
-За якою формулою обчислюється площа криволінійної трапеції на кожному малюнку?
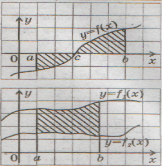
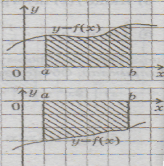
ІІІ. Формування вмінь учнів обчислювати площу криволінійної трапеції.
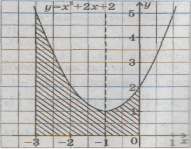
Завдання 1.Обчислити площу фігури, обмеженої лініями: у = х2 + 2х + 2, у = 0, х = 0, х = -3;
у - х2 +2х + 2 - квадратична функція, графік - парабола, вітки - вгору (а =1, а > О). Координати вершини параболи:хв=-1,ув=1
(-1;1) - вершина параболи, х = -1 - вісь симетрії.
Точки перетину параболи з осями координат: з Ох: у = 0, х2 + 2х + 2 =0;
D =1 -2 = -1, D<0; коренів немає.
Парабола з віссю Ох не перетинається.
З Оу: х = 0, у – 02 +2 . 0+2=2; (0;2).
у =О - вісь Ох; х = 0 - вісь Оу;
х = -3 - пряма, що проходить через -3 на осі Ох паралельно осі Оу.
а = 0, b=-3 - межі інтегрування.
![]() 0
0
![]() S=
S=![]() 2+2x+2)dx=
2+2x+2)dx=![]()
![]()
![]() = 0-(-9+9-6) = 6 ( кв.од.)
= 0-(-9+9-6) = 6 ( кв.од.)
Відповідь: 6 кв.од. -3
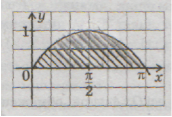
Завдання 2. Обчислити площу фігури, обмеженої синусоїдою
у=sin x і відрізком [0;П] осі ОХ
Спочатку побудуємо графік функції, зафарбуємо область інтегрування .
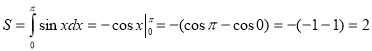 ( кв.од.)
( кв.од.)
Відповідь: 2 кв.од
А тепер давайте виконаємо наші завдання 1та 2 за допомогою комп’ютерної програми .
У вас на робочих столах є папка Gran1.
За допомогою програми Gran1 обчислимо цей самий інтеграл. Для обчислення інтеграла потрібно:
Ввести функцію( Об׳єкт/ Нова функція).
Вводимо функцію і задаємо область визначення.
Побудувати графік введеної функції (Графік/Побудувати).
Інтеграл(F10). Вводимо межі інтегрування, Enter.
На екрані з’являється заштрихована область, це та область, за якою обчислюється інтеграл.
Якщо вам функція вже не потрібна, то її можна вилучити (Об׳єкт/Видалити).
Якщо вам потрібно обчислити площу фігури, обмеженої кривими, то потрібно спочатку ввести ці функції й побудувати їх графіки.
IV . Практична робота.
Робота в парах
Обчислити площі плоских фігур, обмежених:
1)параболою у=х2 і прямою у= 4-х;
2)параболою у=х2 і прямою у=х.
3)параболою у=(х+1)2 і прямою у= х+2;
4)параболою у=х2 +2х-6 і віссю ОХ ;
5) у=соs(x+1); у=соs(x-1).
Учні спочатку обчислюють дані площі за допомогою інтеграла, а потім перевіряють правильність розв’язання за допомогою програми Gran 1.
Після того як завдання виконане, проводиться оцінювання.
v. Підсумок уроку.
Сьогодні на уроці ми вдосконалили свої вміння обчислювати площі плоских фігур, закріпили знання, отримані на минулих уроках.
Ми також ознайомилися та навчилися за допомогою програми Gran 1 будувати графіки і обчислювати інтеграли.
vІ. Домашнє завдання.
”Алгебра 11 в таблицях” С: №7, Д: №9 (а-г) В: №9 (г-ж)ст.66.
1


про публікацію авторської розробки
Додати розробку
