Презентація "Числа Фібоначчі" до проекту "Числові послідовності"

Роботу виконав учень 9-го класу ЗШ І-ІІІст. с. Червоне Карашевич Віталій2018р. Числа Фібоначчі

Мета: виявити застосування чисел Фібоначчі та показати зв’язок ряду чисел Фібоначчі з різними сферами нашого життя. Завдання: ознайомити з історичними даними;показати зв'язок математики з іншими науками;проілюструвати застосування математики в житті.

Леонардо із Пізи, відомий як Фібоначчі, був першим з великих математиків Європи пізнього Середньовіччя. Будучи народженим у Пізі в багатій купецькій сім'ї, він прийшов в математику завдяки суто практичної потреби встановити ділові контакти. У молодості Леонардо багато подорожував, супроводжуючи батька в ділових поїздках. Під час таких поїздок він багато спілкувався з місцевими вченими. Неможливо уявити сучасний бухгалтерський, і взагалі фінансовий, облік без використання десяткової системи числення і арабських цифр, початок використання яких у Європі було покладено Фібоначчі. У 1202 році він видав книгу «Книга абака», яка містила в собі сукупність знань того часу з арифметики і алгебри. Це була одна з перших книг в Європі, яка вчила вживати десяткову систему числення.    Історія чисел Фібоначчі

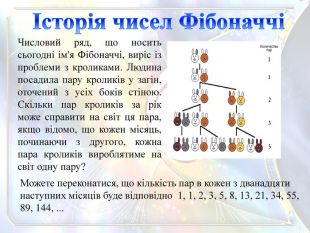
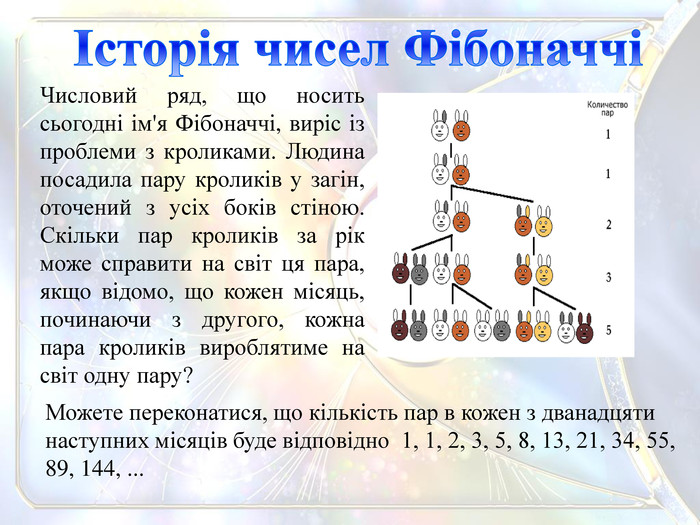
Можете переконатися, що кількість пар в кожен з дванадцяти наступних місяців буде відповідно 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... Історія чисел ФібоначчіЧисловий ряд, що носить сьогодні ім'я Фібоначчі, виріс із проблеми з кроликами. Людина посадила пару кроликів у загін, оточений з усіх боків стіною. Скільки пар кроликів за рік може справити на світ ця пара, якщо відомо, що кожен місяць, починаючи з другого, кожна пара кроликів вироблятиме на світ одну пару?

Фібоначчі склав такий ряд з натуральних чисел, який корисний в науці: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ... і т.д           Закономірність цього ряду проста. Перші два числа - одиниці, а потім кожний наступний член виходить шляхом складання двох безпосередньо йому передують. Наприклад: 2 = 1 + 1, 3 = 1 + 2, 5 = 2 + 3, 8 = 3 + 5 і т.д. Послідовність чисел Фібоначчі

1. Сума кожних двох попередніх дорівнює наступному числу2. Частка наступного і попереднього числа дорівнює 1, 618 (φ).3. Частка попереднього і наступного дорівнює 0,618(починаючи з п'ятого)4. Числа 0,618 і 1,618—обернені5. Кожне третє число — парне6. Кожне четверте — кратне 37. Кожне п'ятнадцяте закінчується нулем8. Кожні два сусідні числа послідовності взаємно прості9. Квадрат будь-якого числа Фібоначчі дорівнює добутку двох сусідніх (попереднього і наступного) чисел плюс чи мінус 1. Квадрати чисел Фібоначчі з непарними номерами (наприклад, 2, 5, 13) на 1 більше добутку двох сусідніх чисел з парними номерами. Квадрати чисел Фібоначчі з парними номерами (наприклад, 3, 8, 21) на 1 менше добутку двох сусідніх чисел з непарними номерами. Властивості чисел Фібоначчі

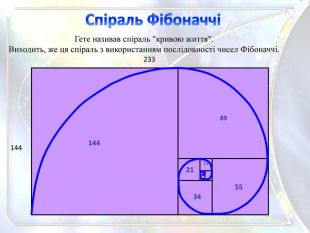
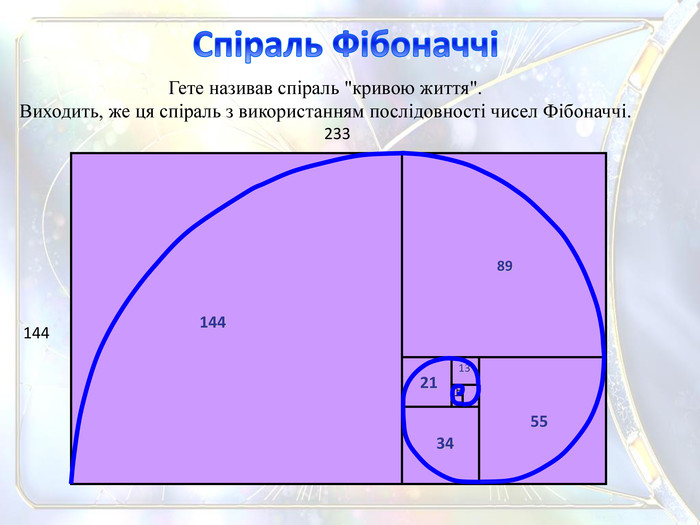
1442331442155348913 Гете називав спіраль "кривою життя". Виходить, же ця спіраль з використанням послідовності чисел Фібоначчі. Спіраль Фібоначчіstyle.colorfillcolorfill.typefill.onstyle.colorfillcolorfill.typefill.onstyle.colorfillcolorfill.typefill.onstyle.colorfillcolorfill.typefill.onstyle.colorfillcolorfill.typefill.onstyle.colorfillcolorfill.typefill.on

Важливо відзначити, що Фібоначчі як би нагадав свою послідовність людству. Вона була відома ще древнім грекам і єгиптянам. І дійсно, з того часу в природі, архітектурі, образотворчому мистецтві, математиці, фізиці, астрономії, біології і багатьох інших областях були знайдені закономірності, описувані коефіцієнтами Фібоначчі.  Однак не буде перебільшенням сказати, що це не просто гра з числами, а найважливіший математичний вираз природних явищ із всіх коли-небудь відкритих. Спіраль ФібоначчіПавук плете павутину спиралеподібно. Спіраллю закручується ураган. Перелякане стадо північних оленів розбігається по спіралі. Молекула ДНК закручена подвійною спіраллю.

Гете говорив про спіральністі навколишнього світу. Спіраль побачили в розташуванні насіння соняшнику, в шишках сосни, ананасах, кактусах і т.д.

Ще одним надзвичайно цікавим явищем є те, що послідовність чисел Фібоначчі можна розгледіти в спіральному розташуванні листя навколо стебла рослини (явище, зветься філлотаксіс). Ця спіральна форма добре помітна, якщо подивитися на стебло зверху і побачити кут розбіжності між листям. У кожному випадку кут розбіжності слідує по ряду чисел Фібоначчі. Таке розташування листя дозволяє кожному листочку отримати максимальну кількість сонячного світла і повітря, при цьому кожен листок не затінює і не стискає сусідні листя. У в’яза кут розбіжності між листям становить 1/2 повного оберту У груші і тополі кут розбіжності становить 3/8 повного оберту У мигдалю і верби кут розбіжності становить 5/13 повного оберту У сосни кут розбіжності становить або 5/21, або 13/34.

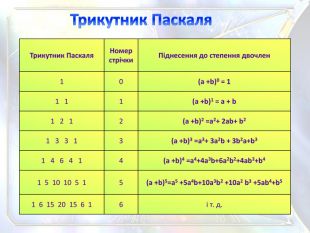
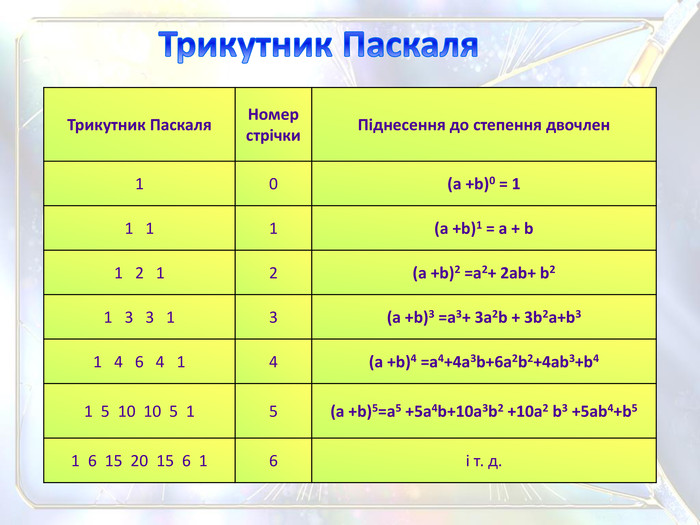
Трикутник Паскаля. Номер стрічки. Піднесення до степення двочлен10(a +b)0 = 11 11(a +b)1 = a + b1 2 1 2(a +b)2 =a2+ 2ab+ b21 3 3 13(a +b)3 =a3+ 3a2b + 3b2a+b31 4 6 4 14(a +b)4 =a4+4a3b+6a2b2+4ab3+b41 5 10 10 5 15(a +b)5=a5 +5a4b+10a3b2 +10a2 b3 +5ab4+b51 6 15 20 15 6 16і т. д.0 1 1 1 12 1 2 1 Трикутник Паскаля

0 1 1 1 12 1 2 13 1 3 3 14 1 4 6 4 15 1 5 10 10 5 16 1 6 15 20 15 6 17 1 7 21 35 35 21 7 1…………………………………1138251321 Трикутник Паскаля

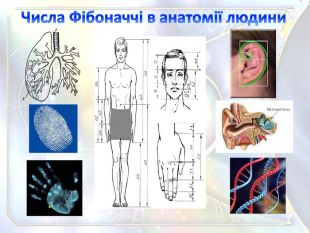
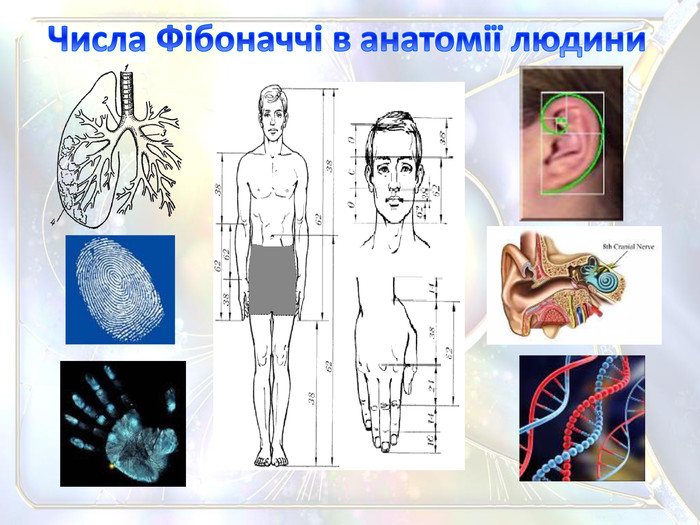
Якщо розглянемо частин людського тіла з боку інвентаризації, то матимемо: У нього один тулуб, одна голова, одне серце і т. д. Багато частини тіла і органи парні, наприклад, руки, ноги, очі, нирки. З трьох частин складаються ноги, руки, пальці рук. На руках і ногах по п'ять пальців, а рука разом з пальцями складається з восьми частин. У людини 12 пар ребер (одна пара атрофована і присутній у вигляді рудимента). Кисть складається з трьох основних частин: зап'ястя, п'ястка і пальців. До складу зап'ястя входить 8 кісточок, воно зчленовується з 5 кістками п'ястка, які складають основу долоні. Кожен палець складається з трьох фаланг: основних, середніх і нігтьових. Хребет людини складається з 34 хребців. Всі ці числа, є числами послідовності Фібоначчі. Числа Фібоначчі в анатомії людини

Числа Фібоначчі в анатомії людини

Фібоначчі ділять наше життя на етапи за кількістю прожитих років:0 - початок відліку - дитина народилася. У неї ще відсутні не тільки психомоторика, мислення, почуття, уява, але і оперативний енергопотенціал. Вона - початок нового життя, нової гармонії;1 - дитина опанувала ходьбу і знайомиться з найближчим оточенням;2 - розуміє мову і діє, користуючись словесними вказівками;3 - діє за допомогою слова, задає питання;5 - «вік грації» - гармонія психомоторики, пам'яті, уяви і почуттів, які вже дозволяють дитині охопити світ у всій його цілісності;8 - на передній план виходять почуття. Їм служить уява, а мислення силами своєї критичності направлено на підтримку внутрішньої і зовнішньої гармонії життя;13 - починає працювати механізм таланту, спрямований на перетворення набутого в процесі успадкування матеріалу, розвиваючи свій власний талант;21 - механізм творчості наблизився до стану гармонії і робляться спроби виконувати талановиту роботу; Числа Фібоначчі в психології

З історії астрономії відомо, що І. Тіціус, німецький астроном XVIII століття, за допомогою ряду Фібоначчі знайшов закономірність і порядок у відстанях між планетами сонячної системи. Числа Фібоначчі можна зустріти і в багатьох шкільних предметах: в хімії, фізиці, інформатиці, музиці за допомогою чисел Фібоначчі навіть можна проаналізувати літературні твори. Вчені продовжують активно розвивати теорію чисел Фібоначчі і золотого перетину. Золота пропорція активно використовується у мистецтві. Закономірність чисел Фібоначчі присутня і в літературі. Закон золотого перерізу найвиразніше проявляється в геніальних авторів, причому „переважно в епоху їхньої повної зрілості і головним чином у кращих, їхніх творіннях”. Дослідники звернули увагу на найвище піднесення поетичного переживання – своєрідну кульмінаційну віху, яка припадає саме на рядок, місцерозположення якого в творі відповідає числу φ

Роль числа φі в літературних творах1) служить моментом розподілу між головними частинами твору і тим самим установлює пропорційні розміри частин твору по відношенню до цілого; 2) підкреслює кульмінаційний пункт зростаючого за напругою очікування; 3) відзначає головну, основну думку твору, розташувавши її на такому помітному для безпосереднього чуттєвого сприйняття місці.

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}«Лісова пісня» Лесі Українки(дзеркальний перетин) 1. Драма-феєрія в 3-х діях2. СПИС ДІЯЧІВ «ЛІСОВОЇ ПІСНІ»3. ПРОЛОГ4. «Той, що греблі рве». Русалка.***1257. Мавко!1258. ти з мене душу виймеш!1259. М а в к а1260. Вийму, вийму!1261. Візьму собі твою співочу душу,1262. а серденько словами зачарую...1263. Я цілуватиму вустонька гожі,* * *2035. На устах застиг щасливий усміх.2036. Він сидить без руху.2037. Сніг шапкою наліг йому на голову, запорошив усю постать2038. і падає, падає без кінця... Дослідники творчості Т. Г. Шевченка, І. Франка,Л. Українки, О. Кобилянської, зауважили пропорційну узгодженість крупних шматків, де „золотий поділ” з постійним коефіцієнтом фі ≈ 0,62 припадає на рядки, в яких виявляється або переломний момент у змісті твору, або основний ідейний акцент.

В архітектурі пропорція є важливим і надійним засобом для досягнення рівноваги між цілим та його частинами. Наприклад, відношення висоти найкрасивіших будівель до їх довжини становить 0,618. Театр в ЕпідавріХрам Артеміди. Театр Діоніса в Афінах. Грецький Парфенон. Шедеври Древньої Еллади

Софія Київська. Спадщина Українських зодчих. Львівський оперний театр. Будинок з химерами, Київ

Золоті пропорції Старого Львова

Числа Фібоначчі в древньому Єгипті Піраміда побудована так, щоб площа кожної з її граней дорівнювала квадрату її висоти. 238,7 : 147,6 = 1, 618 Спостереження показують, що конструкція піраміди заснована на пропорції Ф=1,618.

Американський школяр з Нью-Йорка, Ейдан Дуайер, маючи певні знання про зв’язок ряду чисел Фібоначчі з розміщенням листя на деревах, вирішив підвищити ефективність сонячних електростанцій. Ейдан побудував на своєму задньому дворі дослідну установку з маленькими сонячними батареями замість листя і привів її в дію. Виявилося, що в порівнянні зі звичайною плоскою сонячною панеллю його «дерево» збирає на 20% більше енергії і на 2,5 години довше ефективно працює. Модель сонячного дерева Дуайера, побудовані школярем. Практичне використання чисел Фібоначчі у житті

У даній роботі було розглянуто та проаналізовано прояв чисел послідовності Фібоначчі в оточуючій нас дійсності. Ми переконалися, що у Природи є свої закони, виражені за допомогою математики. І математика - це дуже важливий інструмент для пізнання таємниць природи. Дійсність, яка нас оточує, побудована за гармонійним законом з математичною точністю. Все в світі продумано і прораховано найголовнішим нашим дизайнером - Природою! Усі завдання, які були поставлені - виконані, мета - досягнута. Висновок

Дякую за увагу!