Презентація до уроку засвоєння нових знань з теми "Неповні квадратні рівняння."
Про матеріал
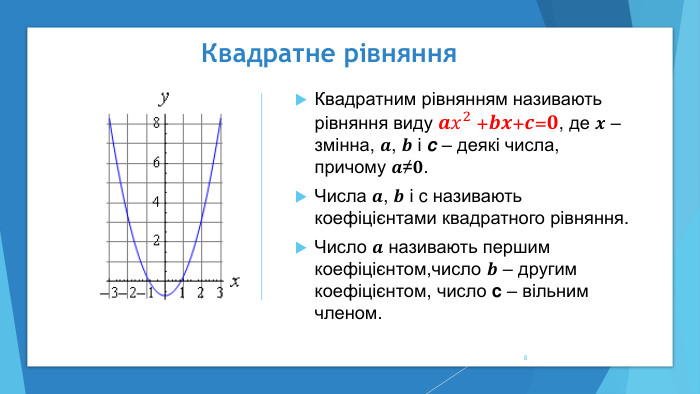
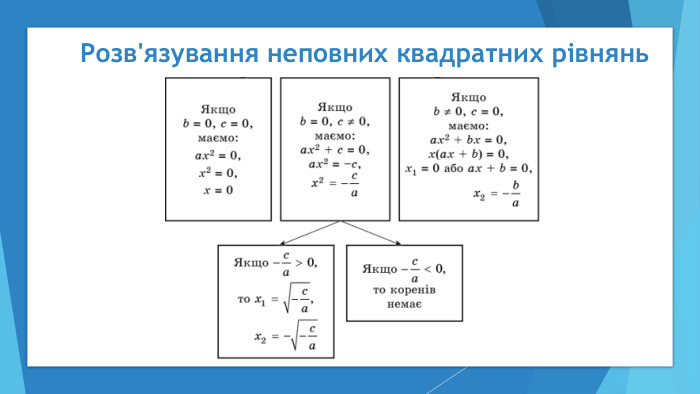
Дана презентація може бути використана при вивченні теми "Квадратні рівняння" у 8 класі для кращого засвоєння матеріалу та розвитку пізнавальної активності учнів.
Матеріал може бути використаний для очних і дистанційних уроків. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку