Творча робота учнів на уроках математики

 

 

 

Творча робота учнів на уроках математики

 

 

 

 

 

 

 

 

 

 

 

Підготувала

Боднар Ольга

 

 

 

 

 

 

 

 

2022

  Справжній скарб для людини – вміння трудитися.

                                                                                      Езоп.

           Серед методів активізації математичної діяльності учнів на уроці в процесі здобуття та закріплення нових знань,творчого застосування їх в різноманітних практичних ситуаціях самостійні письмові роботи з математики займають одне з чільних місць. На уроках математики учні виконують багато тренувальних  вправ, самостійних робіт на закріплення навичок розв’язування задач, прикладів, принципи розв’язку  яких їм уже зрозумілі, робіт, що мають на меті формування певного алгоритму дій  і перетворень,перевірку глибини і міцності знань. Проте всі ці роботи не виводять школяра за межі репродуктивного мислення, бо в більшості випадків він дотримується наведеного вчителем зразка. І тому нерідко буває, що учні, засвоївши лише форму розв’язку, навчившись швидко виконувати подану вчителем послідовність операцій,не до кінця розуміють зміст певного поняття. Ось чому на уроках  тренувальних вправ впроваджую якнайбільше творчих елементів.

           Творча  діяльність учня в процесі виконання таких робіт не обмежується тільки здобуттям, засвоєнням нового матеріалу, вона передбачає створення нового в процесі активної пошукової діяльності.

           Досвід показує, що спонукання школярів до самостійної  діяльності залежить, з одного боку, від цілеспрямованого добору  дидактичного матеріалу, а з другого – від застосування методів, форм роботи, що передбачають створення обставин, за яких кожен учень не тільки зацікавлений, а й поставлений перед необхідністю самостійно розв'язувати поставлену вчителем проблему.

 

 

 

 

 

 

 

 

                                                  I.   Складання рівнянь

         Під час вивчення лінійних рівнянь,нерівностей, систем рівнянь та нерівностей першого степеня з двома невідомими найдопитливіші з учнів часто замислюються над тим , звідки беруться такі рівняння,  нерівності, системи, хто їх складає. Чи змогли б вони самі скласти нове рівняння або систему, умову складної задачі.

        Щоб дати змогу учням самостійно відповісти на такі запитання, я в 7 класі наприклад, проводжу таку  підготовчу роботу.

        Поділивши дошку та відповідно сторінку зошита на дві частини, записуємо:

 

               Ствердження дій                                               Обґрунтування перетворень 

                                        

               Розв'язати рівняння                          

           + = +       * 24                                Умова рівняння

     Звільнимось від знаменників, що                  Властивості рівняння

 містяться   в членах рівняння:

         4(х+1) +3(2-х) = 6+2(х-3)

            Розкриваємо дужки:

               4х+4+6-3х=6+2х-6

    Перенесемо члени, що містять невідоме,       Знаки перенесених членів                                                                                           в ліву, а відомі в праву частину рівняння:        змінюються на протилежні.

         4х-3х-2х=6-6-4-6                                    Властивість рівняння.                                             

    Зведемо подібні доданки: Спрощення виразів.

                  -х = -10 

    Знайдемо значення змінної х                                  Властивість рівності.

                   х =10                                                         

                                                                            

 

         Кожна з операцій, що виконувалась нами в процесі розв’язування рівняння, була зворотна, тому останнє рівняння    х = 10 задовольняє його. В кінці робимо перевірку розв’язку.

        Виконання таких вправ сприяє виробленню навичок аналізу і синтезу. І тому  учні досить легко справляються із завданням: «Скласти рівняння, яке б мало корінь х = 2»

                   Учні записують      

Ствердження дій. Складання рівняння.                

                     х=2                                                               Найпростіше рівняння.

Помножимо обидві частини рівняння на  4             Властивість рівняння.

                      4х=8

Додамо до обох частин рівняння число  7:             Властивість рівняння.

                     4х+7=15

Перетворимо суму в лівій частині

                     (3х+4)+(х+3)=15

Помножимо кожний член рівняння на                          Властивість рівняння.

         +

   Віднімемо від обох частин    дріб                    Властивість рівняння.

  =                                                                      Одержане рівняння.

              Оскільки порядок  виконання перетворень у кожного учня може бути свій, то рівнянь дістаємо, як правило, кілька – тут у тій чи іншій мірі виявляється творчість,індивідуальні нахили, здібності та власний досвід семикласників.  Після складання рівняння учні розв’язують його і впевнюються в еквівалентності  перетворень, у  правильності розв’язку   х = 2.

              На такому уроці учні мають можливість працювати в групі (тобто мати колективну думку), і в парах (де сильніший допомагає слабшому), показати свою індивідуальність.

 

 

 

 

 

                                                  II.     Складання нерівностей.  9 клас.

              Вправи на складання нерівностей у поєднанні із звичайними вправами на розв’язування готових нерівностей дають змогу учням повніше і глибше усвідомити зміст даного поняття. 

              Нерівності першого степеня з однією змінною можна складати на основі послідовного застосування тотожних перетворень і властивостей нерівностей.

              Нехай треба скласти нерівність що має розв’язок     х Є (3;+∞)

 

              х > 3

              2х > 6                                                      Властивість нерівності(2).

              2х-3 > 3                                                      Властивість нерівності(1).

              -3(2х-3) < -9                                              Властивість нерівності(3). 

              12-3(2х-3) < 3

       Нехай треба скласти нерівність другого степеня, що має розв'язком проміжок

                                                                   х  Є  (-2;5)

                  - 2 < х < 5              (1)

                   х+2 > 0, х-5 < 0 (2)

        Перемноживши почленно нерівність (2), дістаємо шукану нерівність другого степеня  

                                 .

        Розв’язок    х  Є  (-2;5)    будуть мати також нерівності, одержані діленням однієї з нерівностей на іншу:

                          

 

 

 

 

 

 

 

                                         III.   Складання систем двох рівнянь з двома змінними.

       Учні   7  класу креслять прямокутну систему координат. Через певні точки, взяті на осях проводять дві довільні прямі,що перетинаються. Координати точки перетину дають розв’язок  системи. Учні за виглядом графіків складають систему, розв’язують її аналітично.

        Наприклад:

                                                     3х + у= 3;

                                                  х - 2у = - 2.     

            Легко зрозуміти, що учень, який складає систему двох лінійних рівнянь, психологічно відчуває необхідність її  перевірки. В цьому випадку функції контролю і розв’язування немов би міняються місцями. Справді, учневі відомий розв’язок  одержаної ним системи рівнянь, а для того щоб впевнитися у правильності складеної системи він не підставляє значення змінних х і у, а розв’язує систему і знаходить їх.

            Складання систем рівнянь та нерівностей:

                  ax =c;                                           ax c;

                    .                                  .  

      учні виконують,   виходячи з числових тотожностей та нерівностей, в яких потім змінюють відповідні однакові числа через х і у і дістають бажану систему.

           У 8 класі бажано складати квадратні рівняння.

           Наприклад:

                                       

                                      -5

           Замінивши відповідно 3 і 2 на  х, матимемо

                                       

                                      -5

           Залишається знайти другий корінь.

          Я, звичайно, не орієнтую учнів на складання складних рівнянь і нерівностей, систем рівнянь. Важлива основна мета – домогтися розуміння того, що властивості рівнянь і тотожних перетворень можуть бути використані двояко: як для розв’язування готових, так і для створення нових рівнянь.

 

                                               IV.     Складання задач.

 

Домашнє завдання.  5 клас  

                  1.Обчислити площу та периметр своєї кімнати. Скласти задачу.

           Наприклад:                                                                                                                                                                                           Довжина кімнати  4,8 м, а ширина на 0,3 м менша. Знайти площу та периметр кімнати.      

               Складаючи таку задачу, на мою думку, учень краще запам’ятає формули обчислення площі та периметра прямокутника.

                     2. Знайти об’єм своєї кімнати виконавши потрібні вимірювання                                                                                                                                                                                                     

                        V = a b c,   а = 4м,     b =5м,    с=3м.                              Виконання даних завдань вимагає від учня певних логічних кроків,дає можливість власного творчого підходу.                                                                                                  

                       В  5 – 6 класах практикую складання задач за малюнками

                                                                                                                                               

                  

              54 км/год.                                             60км/год.

        М                                                     О                                   

                                          

                                                  114

         Кожен  учень сам складає задачу і відповідно у нього виникає потреба розв’язати її.

                    Алгебра 8 клас.

I рівень.         Розгляньте рисунок.

                  V₁                                          V₂ 4 км /год. більше V₁  

           

                     240

                 Використовуючи рисунок, складіть задачу, якщо для її розв’язання складено рівняння

                              4(х+4)+4х=240

                 Розв’яжіть задачу.

                   II рівень.         Розгляньте рисунок.

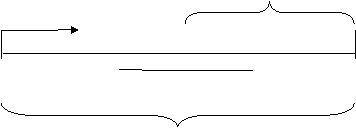                                                V₂ у 2 рази більше від  V₁  

        V₁

 

                                                         70 км. за  5 год. 

                                                                                                                

                  Використовуючи рисунок, складіть задачу, що містить питання: «скільки часу велосипедист затратив на останні 30?»  

                   Розв’яжіть задачу.

                                        III рівень.

              Складіть таку задачу, щоб для її розв’язання можна було використати рівняння :

                        

                  Розв’яжіть задачу.

                   Змініть умову задачі так, щоб для її розв’язання використати рівняння:

                          

 

                                        V.          Перетворення розв’язаних задач.

                Досвід показує, що ефект у розвитку математичного мислення учнів не велика кількість розв’язаних  ними задач,а вдумлива творча робота над обмеженою групою задач або навіть над однією – перетворення її умови,введення нових числових даних. Такі завдання здебільшого пропоную учням виконувати в дома як модифікацію задач, розв’язаних на уроці. Візьмемо як приклад задачу на складання рівняння у 8 класі.

                      Задача .

                Два комбайни можуть зібрати з поля урожай за 8 днів. Коли б один з них зібрав урожай з половини поля, а другий решту, то на збирання врожаю було б витрачено 15 днів. За який час кожний комбайн окремо зможе зібрати урожай з поля?

               Урізноманітнюючи умову, учні змінюють дані про продуктивність комбайнів, кількість комбайнів.

              Наприклад. Два комбайни можуть зібрати з поля урожай за 2 дні. Коли б перший з них зібрав урожай з третини поля, а другий – решту, то всього було б витрачено 9 днів. За який час кожний комбайн окремо зібрав би урожай з поля?

              Переможцями в таких математичних змаганнях виходять ті учні, які складуть найбільшу кількість змістовних модифікацій до умови даної задачі і розв’яжуть їх. Найбільш вдалі задачі записуємо на картки і пропоную слабкішим учням класу для розв’язування. Ефект дуже великий. Автори задач задоволені, що їхня праця потрібна, а слабші учні також з інтересом розв’язують задачі, складені однокласниками.

              Все це загалом дає можливість розвивати творчі здібності учнів, допомагає кожній дитині відчути власну гідність, повірити у свої сили.

              Пропоную вашій увазі приклади двох уроків, щоб продемонструвати описаний вище підхід у роботі з учнями.

       

 

 

 

 

 

 

 

 

 

 

                                                  Математика 5 клас.

 

Тема.   Додавання та віднімання звичайних дробів з однаковими знаменниками.

Мета уроку. Формувати в учнів навики виконання дій віднімання та додавання дробів з однаковими знаменниками; розвивати обчислювальні навики, кмітливість і старанність.

                                                Хід уроку.

I. Вступ.

         Дорогі діти! Сьогодні я вас запрошую в парк «Науки і відпочинку» - додавання і віднімання звичайних дробів з однаковими знаменниками. Я думаю, що ви подружили з дробами і тепер разом сміливо пройдетеся довгою доріжкою Дробових чисел, завітаєте у казкові будиночки.

II. Математична розминка.

        Ось ми бачимо на дверях одного з будиночку вивіску «математична розминка.» Загляньмо в будиночок і виконаємо такі вправи:

1. Як додають дроби з однаковими знаменниками?(віднімають)
2. Наведіть приклади мішаних чисел.
3. Формуйте правило додавання та віднімання дробів з однаковими знаменниками мовою математики.
4. Виконайте дії:

а) ,  , ;

б) 5 , 2 ,1- , 13- , 5 - 2 , 6 -

в)Знайдіть невідоме число:

       ,          .

 

 

 

 

 

г) Знайдіть   від суми цифр, з яких складено малюнок:

                                      

                                                       51

 

 

 

 

 

          

 

 

III. Гра  «Ланцюжок»

 Заходимо в інший будиночок. Нас запрошують пограти в гру «Ланцюжок». На кожну першу парту кожного ряду кладу аркуш паперу, на якому написано вправи на додавання і віднімання дробів з однаковими знаменниками. Кожен учень виконує лише одну вправу і, записавши результат, передає аркуш іншому, поки аркуш не дійде до останнього  учня, який передає його учителю. Який ряд перший виконає все завдання, той і переможе.

                                            

                                           

                                    

IV. Переходимо до іншого будиночку з вивіскою «Задачі і рівняння»

1. Складіть задачі за малюнками:

                               м

 

а)    4 м                                             

 

 

б)      

                                 

                                                                                 

                                                 13       

2. № 1034.Знайдіть корінь   рівняння.

    ,                    

( по одому завданню на кожен ряд)

           Двоє учнів розв’язують рівняння на планшеті,решта учнів виконують те саме завдання в зошитах. По закінчені роботи перевіряють свої розв’язки із   розвязками на планшеті.

3. Задача 1043 (з коментуванням)

4. Задача 1047^*(колективно)

             1) 22*200=4400(грн.) (сума вказаного платежу)

             2)  4400+22=4422(грн.)

V. Цікаві задачі.

Перед нами будиночок з вивіскою «Цікаві задачі.» 

Щоб розв’язати задачу, потрібно дуже уважно прочитати її умову.

1. У млині було шість мишей. Одну мишу кіт зловив. Яка частина мишей залишилась?
2. З V класу, якому 14 учнів, усіх учнів пішло в туристичний похід, а з VI класу стільки, скільки в V залишилося. Скільки всього учнів з цих двох класів пішли в похід?

VI. Самостійна робота.

Всі зручно влаштовуйтеся в останньому будиночку, адже нас чекають завдання на картках.

                                                              

Картка 1.

              Високий рівень.

1. Обчислити:

а)

б)

в)

2. Розв’язати рівняння.

 

Картка 2.

            Достатній рівень.

1. Обчислити:

а)           б)              в)

2. Розв’язати рівняння.

 

Картка 3.

            Середній рівень.

1. Обчислити:

а)                     б)             в)

2. Розв’язати рівняння.

 

VII. Підсумокуроку. Оцінювання учнів.

 VIII. Домашнє завдання.

     Скласти дві задачі на додавання і віднімання дробів з однаковими знаменниками.

Урок математики в 6 класі.

 

Тема. Пропорція. Основна властивість пропорції.

Мета уроку. Закріпити та поглибити знання учнів про відношення та їхні властивості, ввести поняття пропорції, розглянути її основну властивість, вчити застосовувати отриманні знання при розв’язуванні рівнянь, виховувати працьовитість в учнів.

Тип уроку. Урок засвоєння нових знань.

Хід уроку.

1. Актуалізація опорних знань.

Усні вправи ( з чітким коментуванням)

1. Чи можна назвати відношеннями:

24:12 ;   2:5;   7:2;  2,5:10,5?

6м :5;     10дм : 5дм;   7кг:5г;  8кг:8км? 

2. Скласти відношення двох чисел, щоб їхня частка набула значення:

3, 10,.

3. Чи вірні рівності:

26:13=14:7

6:18=5:15

4. Як зміниться відношення, якщо попередній член:

а) збільшити удвічі; збільшити в10 разів;

б) зменшити в 5 разів; зменшити утричі?

5. Як зміниться відношення, якщо наступний член:

а) збільшити утричі;збільшити в 25 разів;

б) зменшити в 4 рази; зменшити в 1,5 разу?

II.          Мотивація, повідомлення теми та матеріалу

              Ви вже знаєте, як часто у повсякденному житті ми зустрічаємось із відношенням (досить часто доводиться зіставляти дві величини, знаходити у скільки разів одна з них більша за іншу.). Але ще частіше ми зустрічаємось і зустрічатимемося надалі із так званими пропорціями. Ви напевно вже використовували їх при розв’язанні задач у молодших і особливо в п’ятому класах (задачі на дроби та відсотки, які тепер ви навчитеся розв’язувати набагато простіше за допомогою схем).

              Тож сьогодні ми починаємо вивчати пропорцію. Ми розглянемо значення пропорції її основну властивість та використання цієї властивості до розв’язання поки що простих вправ, рівнянь та задач, а на наступних уроках ми будемо поглиблювати свої знання та розв’язувати більш складні, але дуже цікаві рівняння та задачі.

III.          Сприймання і засвоєння навчального матеріалу.

       На дошці записані відношення. З даних відношень вибрати ті, які рівні між собою:

                   15:20            18:6           24:4          6:8

                    42:7               3:1            2:4          4:16

                                40:80                  1,4:5,6 

Ви побачили, що рівність двох відношень може бути вірною чи невірною.

     Рівність двох відношень називається пропорцією  

 Наведемо кілька прикладів пропорцій (учні записують у зошитах):

              2:1=10:5               2кг : 4кг = 30л : 60л

            0,5:2=0,75:3           17грн : 1,7грн = 1м : 10см          

За допомогою букв пропорцію можна записати так:

  а :b=c:d               або                      

     (На дошці крайні та середні члени пропорції виділяємо різними кольорами).

            У пропорції  а :b=c:d   числа а і d називають крайніми членами, 

     b і c – середніми членами.

-         Назвіть крайні та середні члени пропорцій:  12:4=27:9,   17:11=34:22, 12:32=6:16.

-         З даних відношень вибрати ті, з яких можна скласти пропорцію:

8:4         25:5      10:2    20:10      12:20

-                     Скласти пропорцію з таких чисел:

а)  9,3,21,7.             б) 100,80,4,5.    

-   Складіть пропорцію, крайні члени якої 2 і 16 а середні 8 і 4.

   2:8 = 4:16, 16:8 = 4:2,   2:4 = 8:16

      Знайдіть добуток крайніх і добуток середніх членів цієї пропорції. Порівняйте їх.

          2*16 = 8*4               16*2=8*4

     У всіх пропорціях добуток крайніх членів дорівнює добутку середніх. 

  Запишемо та запамятаєто: у  правильній пропорції добуток крайніх членів дорівнює добутку середніх членів.

                     а :b=c:d, то    а d= bc

     Це основна властивість пропорції.

IV. Закріплення вивченого матеріалу.

1) усні вправи:

Перевірити основну властивість пропорції:

1:3=6:18         6кг : 9кг = 4:6

2) замінити зірочку цифрою, щоб утворилась вірна рівність:

                                    25:5=35:*

                                    12:18=24:*

                                    15:*=20:8

3) завдання на картках. Запис учні роблять в зошитах (достатній та середній рівень)

Картка 1.

   Замінити зірочки числом:

 *:5=12:4                     8:*=24:6

7:8=14:*

Картка 2.

Перевірити за допомогою основної властивості, чи будуть правильними пропорції(записати у зошит, або – проти кожної з пропорцій):

9:15=3:5

12:7=6:2

5:10=25:8

28:7=24:6

Картка 3.

(достатній та високий рівень)

  Чи вірні відношення (поставте + або - )

5кг:7кг = 10м:14м

10%:100% = 14км:70км

5т:20%=15т:60%

 4) письмові вправи (коментовано на дошці)

   Основна властивість пропорції дає можливість розв’язати рівняння за допомогою основної властивості пропорції:

2:3=5:х,                                                                    

2х=3*5,                                                                      

2х=15,

х=15:2,

х=7,5.

 

24х=6*12,

24х=72,

х=72:24,

х=3.

5) Розв’язування вправ з підручника.

 а) № 667 ( учні записують складені пропорції в зошитах та на дошці)

2;6; 15;5.

2:6=5:15                15:5=6:2

б) № 668(робота в групах по рівнях)

в) №670 а, в. №672 а, б

(відповіді перевірити за розв’язками записаними на дошці).

V. Підсумок уроку. Оцінювання учнів.

  Що називають пропорцією?

Сформулюйте основну властивість пропорції.

Чи використовували ми сьогодні основну властивість пропорції?

VI. Пояснення домашнього завдання.

§4, п.23 № 669(а,б), 671(б,г), 673(а,б)

 

 

  

      

 

                 

     

 

 

 

 

 

 

Усні вправи з теми:

 «Подільність натуральних чисел»

Математика 6 кл

 

 

 

         

 

 

 

 

 

 

                                                      

                     

 

               Однією з ефективних форм організації роботи учнів на уроках математики є систематичне виконання усних вправ на всіх етапах навчання: під час вивчення нового матеріалу, систематизації   та узагальненою  вивченого матеріалу.

          Усні вправи розвивають в учнів уважність спостережливість, ініціативу, збуджують інтерес до математики. Виконуючи усні, вправи, учні не тальки набувають міцних обчислювальних навичок, а  насамперед закріплюють теоретичні знання, тренують увагу і пам'ять ,підвищують свою логічну й загально математичну культуру.

За допомогою усних вправ учитель налагоджує на уроці ефективний оперативний зворотній зв’язок з учнями, що дозволяє своєчасно контролювати процес оволодіня ними знаннями та вміннями.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 1.      Дільники натурального числа.

Актуалізація опорних знань.

1.Що означає поділити 72 на 9; 120 на 40?

2. Яке число потрібно зменшити в 6 раз, що б одержати 60?

3. Ділене 816, частка 8. Знайдіть дільник.

4. Дільник 3, частка 24. Знайдіть ділене.

5.Весьшлях турист пройшов однаковою швидкістю за 2 дні. Першого дня він був у дорозі 7 годин, а другого 4 год. Другого дня турист пройшов на 12 менше, ніж першого. З якою швидкістю йшов турист.

Систематизація та узагальнення вивченого матеріалу.

1.Яке число є дільником будь-якого числа?

2.Які з чисел 2;3;5;7;12;14;15 є дільником числа:

а) 16;                                  б )36.

3.Назвіть дільники числа 19.

4.Як користуючись ємностями 6 л і 8 л, набрати 4 л води?

 

 

 

 

 

 

 

 

 

 

 

 

Урок 2. Ознаки подільності на 2 , 5 і 10.

Актуалізація опорних знань.

1. З даних тверджень вибрати правильне:

а)5 є дільником числа 15;

б)7 є дільником числа 23;

в)16 є дільником числа 48;

г)12 є дільником числа 24;

д)13 є дільником числа 29.

       2. Координати  яких точок є дільниками числа 12 ?

 

О      А    Б     С      Д     Е     К     М   S Р    F     Е    Т

 •      •     •     •     •     •     •     •     •    •     •     •     •     •    

0      1     2     3     4     5     6     7     8      9    10   11  12   13  

 

        3. У хлопчика є 90 коп. Він хоче купити зошити. У магазині зошити коштують 30 коп.,35коп і 45 коп. за один.  Які з наявних зошитів може купити хлопчик за 90 коп. без здачі?

Систематизація та узагальнення вивченого матеріалу.

1. Мама купила 2 кг яблук. Чи може її покупка  коштувати  4 грн. 25 коп.? 4грн. 48 коп.? Пояснити.

2*. На дошці написане число *****7*. Михайлик  і  Віталій по черзі витирають будь-яку зірочку і на її місце записують деяку цифру. Якщо отримане число ділиться на 5,то перемагає Віталій . Чи зможе він перемогти,якщо починає гру ?

3.Чи ділиться сума чисел

                 2³+3³+15 на 10?

4.  Доведіть, що добуток чисел ділиться на 2, 5 і 10.

      42×43×44×45×46×47

 

 

 

 

Урок3. Ознаки подільності на 3 і 9.

Актуалізація опорних знань

1. Які з даних чисел

        172, 804, 901, 2203, 58, 111 не діляться на 2?

2. Переставте у даних числах

        3504; 579; 4008; 653

Цифри так, щоб кожне з них поділилося на 5; на 10.

3. Я хотів провідати хворого товариша і взяв його адресу в канцелярії школи – говорить  Поспішайко. Вулицю запам’ятав , а номер будинку забув. Пам’ятаю  тільки , що він не ділиться на 2. А тільки я його помножив на 5 ,так він і поділився на 2 . А як думаєте, ви діти?

4. Гра «Дільники»

               Учитель називає число і пропонує учням піднести картки із цифрами 2 , 5 і 10,якщо дане число має дільники 2 , 5 або 10. Якщо число має два дільники – підносять 2 картки , 3 – три картки .

Систематизація та узагальнення вивченого матеріалу.

1.Чи правильне твердження:

           якщо число ділиться на 3, то воно ділиться на 9. Сформулюйте правильне твердження.

2. Із чисел 144,676,5724,505 назвіть ті, які не діляться на 3.

3. Праворуч  і ліворуч до числа 18 потрібно дописати по одній цифрі так, щоб одержане число ділилося  на 9.

4.Яку з цифр 5, 8, 2, 1 треба поставити замість зірочки, щоб число 56*5 ділилося на 3 і на 9?

 

 

 

 

Урок  4.Розв’язування вправ на ознаки подільності.

1. Виконати дії та з’ясувати, який із одержаних результатів ділиться на 2, 3, 5, 9, 10.

    а) 0,35÷0,7+44,5;

    б) 1,75+52,25-4;

    в) 12,4×0,5×100;

   г) 8,4÷4+45,9.

2. Яке число ділиться на будь-яке натуральне число?

3. Число ділиться на 2 і не ділиться на 6. Чи  ділиться воно 3?

4. Андрійко знає тільки цифру 1. Доведіть, що він може записати число, яке ділиться на 3; на 9.

5. Назвіть число яке  ділиться на 9 і складається :

      а) тільки з цифр 2;

     б) тільки з цифр 3.

6. Скільки коштує килим? – запитав покупець у продавця.

Вартість його в гривнях - найбільше число першої сотні, яке ділиться на  2, 3 і 5. Яка вартість килима?

7. Як розрахуватись, якщо ти повинен заплатити в касу 19 грн., і в тебе банкноти по 5 грн., а в касира-тільки по  2 грн.?

 

 

 

 

   

 

 

 

 

 

Урок 5. Прості і складні числа.

Актуалізація опорних знань.

1. Число 204 – це добуток чисел 34 і 6. Чи є число 34 дільником числа 204? А число 6?

2.  Не виконуючи додавання, з’ясувати, чи ділиться сума:

                                                      а) 2594+132+476 на 2;

                                                      б) 971+1254+36890 на 5.

3. Назвати всі значення у, які діляться :

                                                      а) на 2 і задовольняють нерівність

                                                                     94 <у ≤102;

                                                     б)  на 9 і задовольняють нерівність

                                                                  115 ≤ у ≤ 128.

                        Систематизація та узагальнення вивченого матеріалу.

1.Не виконуючи дій, скажіть, якими числами: простими чи складними є значення  виразу:

                                                                   а) 13×11×4-4;

                                                                   б) 19×5×2+5.

2. Назвіть :

                 а) всі прості  числа, які більші від 12 менші 28; 

                 б) всі складні числа, які більші від 25 і менші від 35.

3*. Число 19 подайте через суму трьох різних чисел.

4. Яке з наступних тверджень є правильним:

                  а) кожне натуральне число є або простим  або складним;

                 б) якщо натуральне число не є простим, то воно складне;

                 в) якщо натуральне число не є простим і більше за 1, то воно складне;

                 г)якщо жодний з доданків не ділиться націло на деяке число, то їх сума теж не ділиться на це число.

 

 

Урок 6. Розкладання натуральних чисел на прості множники .

Актуалізація опорних знань.

Математичний диктант.

1. Заповнити пропуски в записах:

    а) простим називається натуральне число, яке має …  дільники ;

    б) складним називається натуральне число, яке має … ;

    в) число … не є ні простим, ні складним .

2. Записати всі дільники числа і визначити, яким є це число : простим чи складним

           25     17      18     59

3.Користуючись таблицею простих чисел  , серед  даних чисел підкреслити однією лінією прості  числа , двома лініями – складні:

          345; 603; 521;439; 153; 821;  983; 923; 233.

4.Пояснити, чи правильним є твердження, що всі парні числа складені.

                        Систематизація та узагальнення вивченого матеріалу.

1.Розкладом числа 12 на прості множники  є добуток:

   а) 2×2×3×3;   б) 2×6 ;  в) 2×2×3 ; г) 4×3.

2. Розкладіть на прості множники:

            9 ; 10 ; 16 ; 20.

3. Знайдіть числа , які представлені у вигляді добутку простих множників :

 а)2×3×7; б) 5×7×11.

4. Літак летить за вітром зі швидкістю 720 км/год.,а проти вітру такої самої сили – зі швидкістю 712км/год..Чому дорівнює  швидкість вітру ?

Урок 7. Найбільший спільний дільник. Взаємно прості числа.

Актуалізація опорних знань.

1.Знайти числа, які представлені у вигляді добутку простих множників

 

 

 

 

 

 

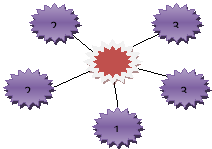
2.Скільки всього дільників має число а, якщо а=3×5×19.

3. Деяке число ділиться на 24 . На які ще числа ділиться це число.

4. На дошці зображено таблицю. Учні з місця називають потрібні числа, а вчитель вносить їх у таблицю.

Число	Дільники
16	1,2,4,8,16
24	1,2,3,4,6,8,12,24

 

5. До якого простого числа треба додати 2, щоб дістати також просте число. Знайдіть кілька таких чисел?

Систематизація та узагальнення вивченого матеріалу.

1. Назвати три числа, які діляться на обидва дані числа:

             а) 2 і 3 ; б) 2 і 5.

2. Знайдіть найбільший  спільний дільник чисел:

а) 15 і 25 ;б) 39 і 17 ; в) 18 і 36 г) m=2×5×7 ; n=2×3×7×11.

3.Чи є взаємно простими числа:

    5 і 15 ; 9 і 17; 14 і 21.

4. З даних пар чисел вибрати взаємно прості:

а) 2 і 8; б)4 і 9; в)49 і 10 ; г) 160 і 200.

5. У парку посадили каштани і дуби, причому на кожний каштан припадало 3 дуби. Скільки всього

дерев посадили  в парку, якщо дубів посадили 24 ?

Урок 8. Кратні натурального числа. Найменше спільне                    кратне.

Актуалізація опорних знань.

1. Дільники числа m : 1; 2; 3; 7; 14; 21. ;       n:1; 2; 3; 11; 22; 33 .

Назвіть спільні дільники  і найбільший спільний дільник.

2. Знайдіть найбільший спільний дільник:

а)       144  2        192  2                           б )          70  2     56  2

            72   2                                    96   2                                         35    5                               28  2

            36   2                                    48   2                                           7     7                               14  2

             18  2                                    24   2                                           1                                        7  7

              9   3                                    12   2                                                                                      1          

              3   3                                      6    2

              1                                            3   3

                                                            1

3.  Назвіть всі правильні  дроби зі знаменником  16, у яких чисельник і знаменник взаємно прості числа.

4. Число 16 подайте як суму дох взаємно простих чисел.

 Систематизація та узагальнення вивченого матеріалу.

1. Використовуючи по одному разу цифри 3, 4, 5 і 6. Складіть два різних трицифрових числа, кожне з яких кратне 3.

2. Чи є число  16 спільним кратним чисел: 4 і 8;  3 і 8.

3. Знайдіть найменше спільне кратне чисел:

а) 2 і 3 ;   б) 2 , 3 і 5 .

4.У скільки разів найбільший спільний дільник даних чисел менший від їх найменшого спільного кратного:

               28 2                                42  2

              14  2        21  3

                7   7                                7    7

                1         1

 

Урок 9. Розв’язування вправ на НСД і НСК.

1.Заповніть пропуски:

    а) кратним натуральному числу  а називається натуральне число, …  .

    б) найменшим спільним кратним  натуральних чисел  а і b називається …  натуральне число, яке … .

   в) найменше спільне кратне двох взаємно простих чисел дорівнює … цих чисел.

    г)       НСК (3, _ )=6

              НСК (4, _ )=12

              НСК (9, _ )=45

             НСД (14, _ )=7

2. Знайдіть найменше спільне кратне і найбільший спільний дільник чисел 8 і 12.

3. Яке з тверджень є правильним :

  1) число  45 – спільне кратне чисел 5 і 9;

  2) число  45 – найменше спільне кратне чисел  5 і 9;

  3) число  45 – спільне кратне чисел 3 і 15;

  4) число  45 – найменше спільне кратне чисел 3 і 15?

4. Записати, якщо це можливо, в кожну з клітинок таблиці по одному числу, яке задовольняє умову:

Число	Парне	Непарне	Кратне 2	Кратне 3	Кратне 5	Кратне 9	Кратне 10
Просте
Складне

 

5. Хлопці помітили: щоб назвати двоцифрове число, потрібна секунда. Петрик називає числа від 30 до 50 і пропускає числа кратні  3, а Сергійко називає числа від 51 до 70 і пропускає числа кратні 4.Скільки секунд витрачає кожний для називання чисел?  (14с. і 15с.)

      Вказівки до розв’язування вправ .*

   Урок 2

                  2*. Згідно з ознакою подільності  дане число ділиться на 5, коли запис числа закінчується цифрою 0 або 5. Тобто Віталію потрібно першим  ходом  останню зірочку замінити на 0 або 5. Тоді він переможе за будь – якої гри Михайлика.

   Урок 3.

                3.*Помилися. Якщо непарне число помножити на непарне, то дістанемо число непарне.

    Урок  4.

               7.* 5×5-3×2=19.

      Урок 5.

               3*19=3+5+11.