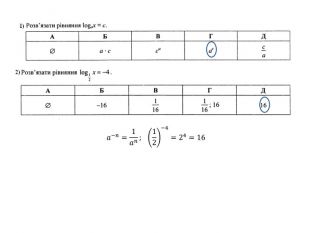
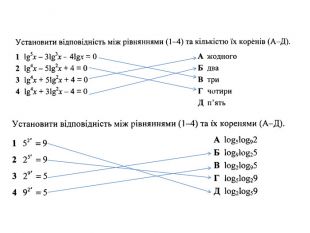
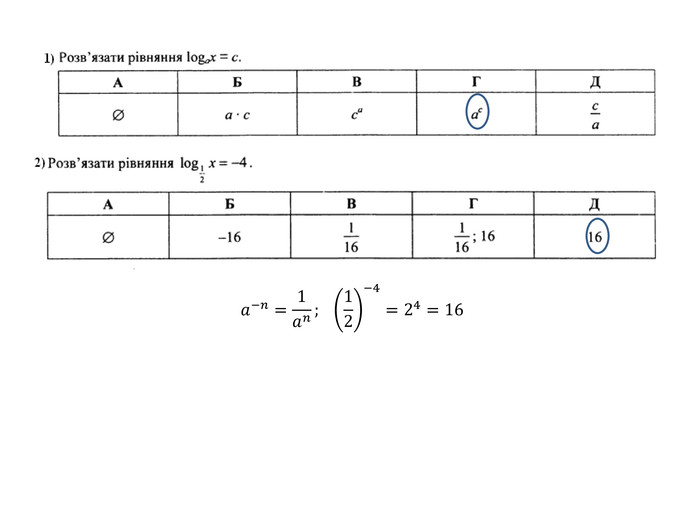
Презентація "Рівняння"

РІВНЯННЯКостюкевич П. П. НВК: ЗОШ №34 –економіко-правовий ліцей «Сучасник» м. Кропивницький

Цілі рівняння

2010. Тарас може доїхати на велосипеді від села до станції за 3 год, а пішки дійти за 7 год. Його швидкість пішки на 8 км/год менша, ніж на велосипеді. Знайдіть відстань від села до станції ( у км). X км/год – швидкість пішки; (x + 8) км/год – швидкість на велосипеді7𝑥=3(𝑥+8)4𝑥=24;𝑥=6𝑆=7∙6=42 

2006. Розв’яжіть рівняння: 𝑥2−𝑥−6=−2𝑥 . Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має декілька коренів, то запишіть їх добуток. Підносимо до квадрату: 𝑥2−𝑥−6=−2𝑥𝑥2+𝑥−6=0𝐷=1−4∙−6=25𝑥1=−1−52=−3𝑥2=−1+52=2 - не корінь, оскільки −2∙2<0 Зауваження. При розв'язанні ірраціональних рівнянь необхідно враховувати ОДЗ. Але шукати його не обов'язково, оскільки кількість розв’язків є обмеженою. Головне не забути зробити перевірку. При піднесенні до квадрату практично завжди отримаємо сторонні корені

2007. Розв’яжіть рівняння: 𝑥2−9−15+8𝑥−𝑥2=0. У відповідь запишіть суму коренів.𝑥2−9=0;𝑥−3𝑥+3=0𝑥1=3; 𝑥2=−3 – не є розв'язком, оскільки при підстановці в підкореневий вираз отримаємо від'ємне число −15+8𝑥−𝑥2=0 ∙(−1)𝑥2−8𝑥+15=0 Сума коренів 88 + 3 = 11 

2008. Розв’яжіть рівняння 𝑥−5+2𝑥2−14𝑥+13=0. Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток.2𝑥2−14𝑥+13=5−𝑥 (*)Підносимо до квадрату: 2𝑥2−14𝑥+13=(5−𝑥)22𝑥2−14𝑥+13=25−10𝑥+𝑥2𝑥2−4𝑥−12=0𝐷4=4+12=16𝑥1=2−4=−2𝑥2=2+4=6 – не корінь, бо при підстановці в (*) в правій частині отримаємо від'ємне число, а 𝑡≥0 

2010. Розв’яжіть рівняння. Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше одного кореня, то у відповідь запишіть добуток усіх його коренів. 2𝑥−1−3=5     2𝑥−1+3=5      2𝑥−3+1=52𝑥−1−3=−5 або 2𝑥−1−3=52𝑥−1=−2 або 2𝑥−1=8𝑥∈∅ 2𝑥−1=−8;2𝑥−1=8 𝑥1=−72;  𝑥2=92 𝑥1∙𝑥2=−7∙92∙2=−634=−1534=−15,75 

Раціональні рівняння

𝑥+2≠0;𝑥−3≠0⇒𝑥≠−2;𝑥≠32𝑥−2𝑥−3+𝑥+3𝑥+2−5𝑥+2𝑥−3=02𝑥2−8𝑥+6+𝑥2+5𝑥+6−5𝑥2+5𝑥+30=0−2𝑥2+2𝑥+42=0 :(−2)𝑥2−𝑥−21=0𝐷>0;𝑥=−2;𝑥=3 – не є коренями останнього рівняння. За теоремою Вієта: 𝑥1+𝑥2=1 

𝑥≠±22𝑥2−4𝑥+𝑥+2=42𝑥2−3𝑥−2=0𝐷=9−4∙2∙−2=25𝑥1=3−52∙2=−0,5𝑥2=3+52∙2=2 – не корінь 

𝑥≠0;𝑥≠±33(𝑥−3)(𝑥+3)−1𝑥−32−32𝑥𝑥+3=0 Спільний знаменник: 2𝑥(𝑥+3)(𝑥−3)23∙2𝑥𝑥−3−2𝑥𝑥+3−3∙𝑥−32=0𝑥2−6𝑥−27=0𝑥1=−3 – не корінь𝑥2=9  

54𝑥2+𝑥+1−3𝑥𝑥−1𝑥2+𝑥+1−12𝑥−1=0 Спільний знаменник: 4𝑥−1𝑥2+𝑥+1;𝑥≠15𝑥−1−12𝑥−2𝑥2+𝑥+1=02𝑥2+9𝑥+7=0𝐷=81−4∙2∙7=25𝑥1=−9−54=−72=−3,5≠1𝑥2=−9+54=−1≠1𝑥1<𝑥2 

𝑥2+𝑥−5𝑥=𝑡;𝑡+3𝑡+4=0 ∙𝑡;𝑡2+4𝑡+3=0𝑡1=−1; 𝑡2=−3𝑥2+𝑥−5=−𝑥; 𝑥2+2𝑥−5=0𝑥1∙𝑥2=−5 (Важливо: корені 𝑥1; 𝑥2 не перетворюють на нуль знаменники даного рівняння)2) 𝑥2+𝑥−5=−3𝑥; 𝑥2+4𝑥−5=0; 𝑥3∙𝑥4=−5𝑥1∙𝑥2∙𝑥3∙𝑥4=−5∙−5=25 

𝑥2+2𝑥−3=0⇒𝑥2+2𝑥−8=𝑡−524𝑡−5−15𝑡−2=0 (𝑡≠0;𝑡≠5)24𝑡−15𝑡+75−2𝑡2+10𝑡=02𝑡2−19𝑡−75=0𝐷=(−19)2−4∙2∙−75=361+600=961=312𝑡1=19−314=−3; 𝑡2=19+314=252 Маємо два квадратні рівняння: 𝑥2+2𝑥=0 та𝑥2+2𝑥−3−252=0 , корені яких не перетворюють на нуль знаменники даного рівняння. Сума коренів (теорема Вієта): −2−2=−4 

𝑥+12𝑥−12=𝑡≥0; 𝑡2−8𝑡−9=0𝑡1=−1<0; 𝑡2=9𝑥+12𝑥−1=−3;𝑥+1=−6𝑥+3;7𝑥=2𝑥+12𝑥−1=3;𝑥+1=6𝑥−3;5𝑥=4;𝑥=0,8 Корінь першого рівняння 27 не може бути записаний у відповідь в принципі (мова йде про завдання другої частини ЗНО). Некоректно з точки зору математики як науки, але корисно з точки зору «НЕЗАЛЕЖНОГО оцінювання»  

𝑥 км/год та (𝑥+20) км/год – швидкості автобуса й автомобіля відповідно. Тоді витрачений час: 60𝑥 та 60𝑥+20 (час в годинах)Автомобіль витратив на 20 + 10 = 30 хвилин менше. Необхідно (!!!) хвилини записати в годинах: 30 хв= 12 год60𝑥−60𝑥+20=0,5120𝑥+120∙20−120𝑥=𝑥2+20𝑥𝑥2+20𝑥−2400=0;𝐷4=100+2400=2500𝑥1=−10−50<0; 𝑥2=−10+50=40 

𝑛 – кількість деталей за планом; 272𝑛 - кількість днів за планом. Понад норму бригада працювала 272𝑛−11 днів10𝑛+272𝑛−11𝑛+4=280 ∙𝑛10𝑛2+272−11𝑛𝑛+4−280𝑛=0𝑛2+52𝑛−4∙272=0𝐷4=262+1088=1764=422𝑛1=−26−42<0; 𝑛2=−26+42=16 

𝑡1∙𝑡2𝑡1+𝑡2 - час сукупної роботи𝑥 годин – час роботи першої труби𝑥(𝑥+5)2𝑥+5=6𝑥2−7𝑥−30=0𝐷=49+120=169𝑥1=7−132<0; 𝑥2=7+132=10 

2013. Розв’яжіть рівняння: 2𝑥𝑥+2=5(𝑥+2)СКОРОЧЕННЯ – це ПОМИЛКА2𝑥𝑥+2−5𝑥+2=02𝑥−5𝑥+2=0𝑥1=2,5; 𝑥2=−2 

2017. Автобус вирушив з міста А до міста В, відстань між якими становить 150 км. Через 30 хв із міста А до міста В тією самою дорогою вирушив автомобіль, швидкість якого в 115 раза більша за швидкість автобуса. Скільки часу (у год) витратив на дорогу з міста А до міста В автомобіль, якщо він прибув до міста В одночасно з автобусом? Уважайте, що автобус та автомобіль рухалися зі сталими швидкостями.𝑥 км/год – швидкість автобуса; 115𝑥 км/год – швидкість автомобіля. Час: 150𝑥 та 15065𝑥=125𝑥 для автобуса і автомобіля відповідно (вимірюється в годинах). 30 хвилин = 0,5 години150𝑥−125𝑥=0,5;0,5𝑥=25;𝑥=50 (швидкість автобуса), тоді витрачений час автомобіля: 12550=2,5  

2018. У майстерні мали виготовити 240 стільців за n днів, причому щодня планували виробляти однакову кількість стільців. Однак, на прохання замовника, завдання виконали на 2 дні раніше запланованого терміну. Для цього довелося денну норму виготовлення збільшити на 4 стільці. Визначте n.240𝑛−2−240𝑛=460𝑛−60𝑛+120=𝑛(𝑛−2)𝑛2−2𝑛−120=0𝐷4=1+120=121𝑛1=1−11<0;𝑛2=1+11=12 

Показникові та логарифмічні рівняння

4)

Рівняння квадратне відносно 2𝑥>0 Необхідно, щоб 𝐷=(𝑎+1)2−1=𝑎2+2𝑎>0𝑎∈(−∞;−2)∪(0;∞)2𝑥=−𝑎−1−𝑎2+2𝑎22𝑥=−𝑎−1+𝑎2+2𝑎2 Перше рівняння сукупності при 𝑎∈(0;∞) розв’язків немає𝑎=−3:2−3>0 Відповідь: −3 

Підстановка: 2𝑥=𝑡>04𝑡+2−1𝑡−3=24𝑡−12−𝑡−2=2𝑡2−𝑡−62𝑡2−5𝑡+2=0𝐷=25−4∙2∙2=9𝑡1=5−34=12⇒2𝑥=2−1;𝑥1=−1𝑡1=5+34=2⇒2𝑥=21;𝑥2=1𝑥1+𝑥2=0 

81𝑥=9𝑥2; 64𝑥=8𝑥2; 72𝑥=9𝑥∙8𝑥Розділемо дане рівняння на 8𝑥2>08∙982𝑥−17∙98𝑥+9=0 – квадратне рівняння відносно 98𝑥 має корені 1 та 9898𝑥=1; 𝑥1=0;98𝑥=98; 𝑥2=1𝑥1+𝑥2=1 

𝑐𝑜𝑠2𝑥=2𝑐𝑜𝑠2𝑥−112∙22𝑐𝑜𝑠2𝑥−3∙2𝑐𝑜𝑠2𝑥+4=0 – рівняння квадратне відносно 2𝑐𝑜𝑠2𝑥=𝑡𝐷=9−4∙12∙4=1𝑡1=3−12∙12=2; 2𝑐𝑜𝑠2𝑥=2; 𝑐𝑜𝑠2𝑥=1;𝑥=𝜋𝑛,𝑛∈ℤ𝑡2=3+12∙12=4; 2𝑐𝑜𝑠2𝑥=4; 𝑐𝑜𝑠2𝑥=2;𝑥∈∅Найменший додатний корінь отримаємо при 𝑛=1𝜋𝜋=1 

7−20𝑥+1=7∙72−5𝑥Нехай 7−5𝑥=𝑡>07𝑡2−50𝑡+7=0𝐷4=252−7∙7=625−49=576=242𝑡1=25−247=17⇒7−5𝑥=7−1⇒𝑥∈∅𝑡1=25+247=7⇒7−5𝑥=71⇒−5𝑥=1;𝑥=−0,2 

2007. Розв’яжіть рівняння: 38𝑥=2∙32 2008. Розв’яжіть рівняння: 3𝑥=2362010. Якому проміжку належить корінь рівняння: 2𝑥=18 А (-6; -4] Б (-4; -2] В (-1; 1] Г (2; 4] Д (7; 9]2011. Якому з наведених нижче проміжків належить корінь рівняння 5𝑥+2=1125𝑥А (-3; -2] Б (-2; -1] В (-1; 0] Г (0; 1] Д (1; 3] 

2015. Розв’яжіть рівняння: 4𝑥=82017. Розв’яжіть рівняння: 22𝑥=123 2013. 3𝑥∙4𝑥=12𝑥+1512𝑥=125𝑥+5𝑥=5𝑥+5−4𝑥=5𝑥=−54=−114=−1,25 

𝑎−𝑛=1𝑎𝑛;   12−4=24=16 

1−𝑙𝑔5=𝑙𝑔10−𝑙𝑔5=𝑙𝑔105=𝑙𝑔2 𝑙𝑔𝑥2−𝑥=𝑙𝑔2⇒𝑥2−𝑥−2=0; 𝑥1=−1;𝑥2=2 

(2010) Якому з наведених проміжків належить корінь рівняння 𝑙𝑜𝑔3𝑥=2?(-4; -1] (-1; 2] (2; 5] (5; 8] (8; 11](2018) Яке з наведених чисел є коренем рівняння 𝒍𝒐𝒈𝟒𝒙−𝟏=𝟑?4 13 63 65 82 𝑥−1=43=64;𝑥=64+1=65 

𝑙𝑜𝑔2𝑙𝑜𝑔3𝑙𝑜𝑔4𝑥=0⇒𝑙𝑜𝑔3𝑙𝑜𝑔4𝑥=20=1⇒ ⇒𝑙𝑜𝑔4𝑥=31=3⇒𝑥=43=64 

𝑥1 та 𝑥2 - корені рівняння, тоді   𝑙𝑜𝑔2𝑥1+𝑙𝑜𝑔2𝑥2=𝑙𝑜𝑔2𝑥1𝑥2 𝑥1∙𝑥2=2−коефіцієнт перед 𝑙𝑜𝑔2𝑥 

𝑙𝑜𝑔7𝑥−2+𝑙𝑜𝑔72𝑥−7=𝑙𝑜𝑔77+𝑙𝑜𝑔7(𝑥+2)𝑙𝑜𝑔72𝑥2−11𝑥+14=𝑙𝑜𝑔7(7𝑥+14)2𝑥2−11𝑥+14=7𝑥+142𝑥2−18𝑥=0;2𝑥𝑥−9=0𝑥1=0 – сторонній корінь𝑥2=9  

𝑙𝑜𝑔5(𝑥−5)(𝑥−5)(𝑥+5)𝑥+5=0𝑙𝑜𝑔5(𝑥−5)2=0;(𝑥−5)2=1𝑥−5=1;𝑥=6𝑥−5=−1;𝑥=4 – стороній корінь, оскільки 4−54+5<0 

𝑙𝑔2𝑥4=𝑙𝑔𝑥42=4lg⁡|𝑥|2=16𝑙𝑔2|𝑥|𝑙𝑔𝑥14=14lg⁡|𝑥|lg𝑥=𝑡;16𝑡2−14𝑡−2=0;8𝑡2−7𝑡−1=0𝑡1=1;lg𝑥=1;𝑥=10;𝑥1=−10; 𝑥2=10𝑡2=−18;lg𝑥=−18;𝑥=1810<10  

𝑙𝑔2−𝑥−8lg−𝑥+16=0lg−𝑥−42=0−𝑥=104; 𝑥0 :1000=−10 

1+𝑙𝑔𝑥+10−2𝑙𝑔𝑥=5−𝑙𝑔𝑥1+𝑙𝑔𝑥 𝒍𝒈𝒙≠𝟓;𝒍𝒈𝒙≠−𝟏𝑙𝑔2𝑥−5𝑙𝑔𝑥+6=0𝑙𝑔𝑥=2;𝑥1=100𝑙𝑔𝑥=3;𝑥2=1000𝑥1−𝑥2=𝑥2−𝑥1=900 

𝑙𝑔2100𝑥=2+𝑙𝑔𝑥2=4+4𝑙𝑔𝑥+𝑙𝑔2𝑥𝑙𝑔210𝑥=1+𝑙𝑔𝑥2=1+2𝑙𝑔𝑥+𝑙𝑔2𝑥𝑙𝑔1𝑥=𝑙𝑔1−𝑙𝑔𝑥=−𝑙𝑔𝑥2𝑙𝑔2𝑥+7𝑙𝑔𝑥−9=0𝑙𝑔𝑥=1;𝑥=10𝑙𝑔𝑥=−4,5 

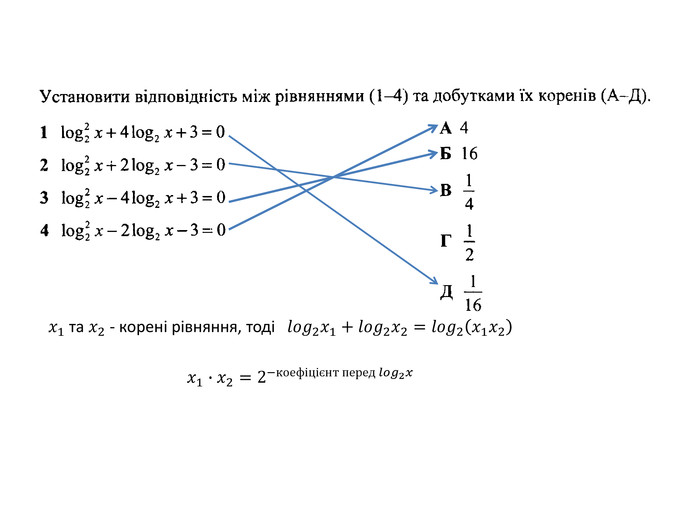
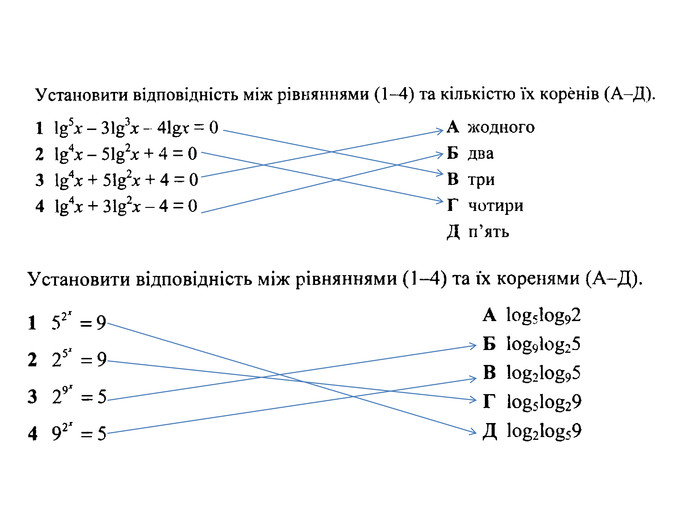
Знайдіть усі значення параметра а , при яких добуток коренів рівняння 𝑙𝑜𝑔22𝑥−2𝑎2−𝑎𝑙𝑜𝑔2𝑥+1−2𝑎=0 дорівнює 8. Якщо таке значення одне, то запишіть його у відповідь. Якщо таких значень більше одного, то у відповідь запишіть найменше з них. Нехай 𝑡=𝑙𝑜𝑔2𝑥⇒𝑥=2𝑡. Якщо 𝑥1 та 𝑥2 – корені даного рівняння, то 𝑥1∙𝑥2=2𝑡1∙2𝑡2=8⇒𝑡1+𝑡2=3. Для квадратного рівняння 𝑡2−2𝑎2−𝑎𝑡+1−2𝑎=0 за теоремою Вієта маємо: 𝑡1+𝑡2=2𝑎2−𝑎=3 2𝑎2−𝑎−3=0⇒𝑎1=−1;𝑎2=32 Перевірка: 1) 𝑡2−3𝑡+3=0⇒𝑡∈∅ 2) 𝑡2−3𝑡−2=0⇒𝑡1+𝑡2=3, 𝑥1∙𝑥2=8 Відповідь: 1,5 

(2006) Задано рівняння: 1) 𝑙𝑜𝑔2𝑥−𝑙𝑜𝑔2𝑥−2=1; 2) 𝑐𝑜𝑠𝑥=1−3 ; 3) 𝑥+2=−34) 𝑠𝑖𝑛𝑥+𝜋3=−𝜋 . Вказати ті, що не мають коренів 

(2007) Знайдіть найменше ціле значення параметра 𝑎, при якому рівняння 𝑙𝑜𝑔8𝑥+2=𝑙𝑜𝑔8(2𝑥−𝑎) має корені. 𝑥+2=2𝑥−𝑎⇒𝑥=𝑎+2𝑎+4>0;𝑎>−4; 2𝑎+2−𝑎=𝑎+4;𝑎>−4  −3 

(2009) Розв’яжіть рівняння: 𝑙𝑜𝑔6𝑥−3+𝑙𝑜𝑔6𝑥−8=2. Якщо рівняння має один корінь, то запишіть його у відповідь; якщо воно має два корені, то у відповідь запишіть їх суму.𝑙𝑜𝑔6𝑥2−11𝑥+24=2𝑥2−11𝑥+24=36𝑥2−11𝑥−12=0 𝑥1=−1 – не корінь, бо −1−3<0𝑥2=12 

(2013) Знайдіть значення параметра 𝑎 , при якому корінь рівняння lg𝑠𝑖𝑛5𝜋𝑥=16+𝑎−𝑥 належить проміжку 32;2. lg𝑠𝑖𝑛5𝜋𝑥≤𝑙𝑔1=0;16+𝑎−𝑥≥0⇒ ⇒𝑠𝑖𝑛5𝜋𝑥=116+𝑎−𝑥=0⇒𝑥=110+25𝑛,𝑛∈𝑍𝑎=𝑥−16 32<110+25𝑛<2⇒72<𝑛<194⇒𝑛=4 𝑥=110+85=1710=1,7⇒𝑎=1,7−16=−14,3 Відповідь: - 14,3 

(2014) Розв’яжіть рівняння: 𝑙𝑜𝑔0,45𝑥2−8=𝑙𝑜𝑔0,4(−3𝑥). Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має декілька коренів, то у відповідь запишіть їх суму.5𝑥2−8=−3𝑥5𝑥2+3𝑥−8=0𝑥1=1 – не корінь, бо −3<0𝑥2=−85=−1,6 

(2015) Розв’яжіть рівняння: 𝑙𝑜𝑔52𝑥+𝑙𝑜𝑔5𝑥=2 (𝑙𝑜𝑔52𝑥−𝑙𝑜𝑔5𝑥=2; 𝑙𝑜𝑔52𝑥−2𝑙𝑜𝑔5𝑥=3)  . Якщо рівняння має один корінь, запишіть його у відповідь. Якщо рівняння має декілька коренів, то запишіть у відповідь їх суму. Якщо рівняння не має коренів, то у відповідь запишіть число 100.𝑙𝑜𝑔52𝑥+𝑙𝑜𝑔5𝑥−2=0𝑙𝑜𝑔5𝑥=1;𝑥1=5𝑙𝑜𝑔5𝑥=−2;𝑥2=5−2=125𝑥1+𝑥2=5+125=5,04