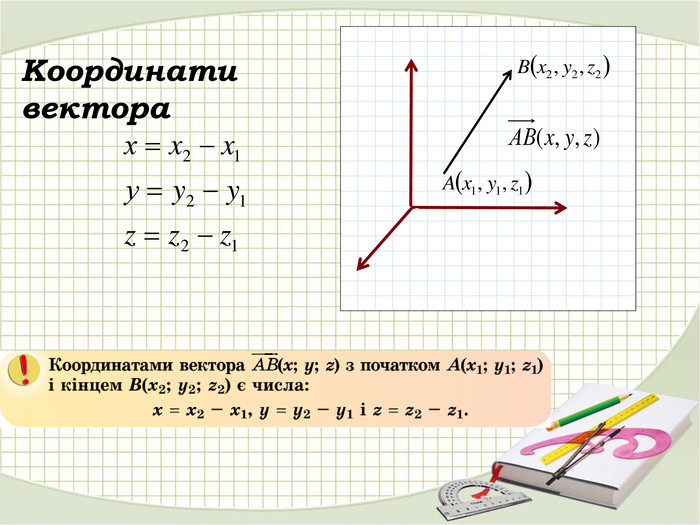
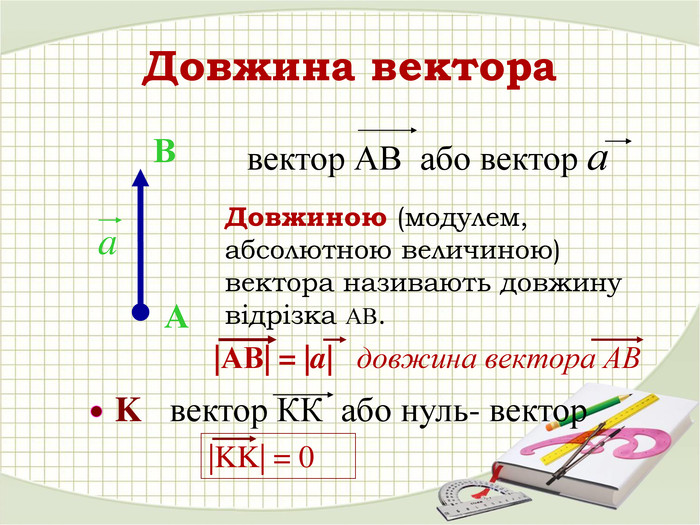
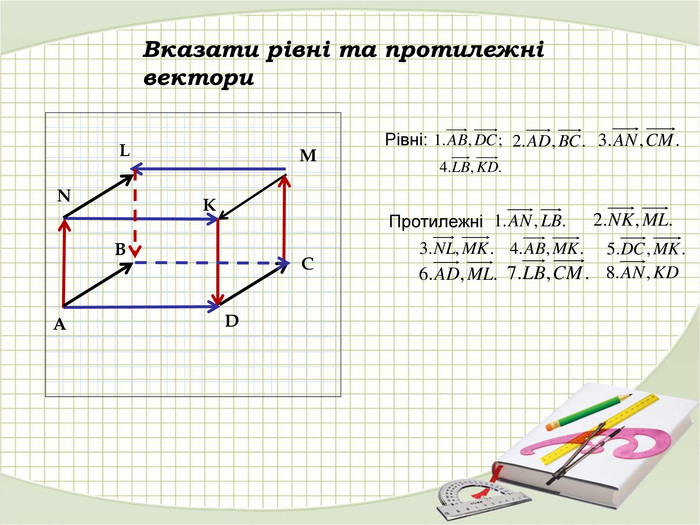
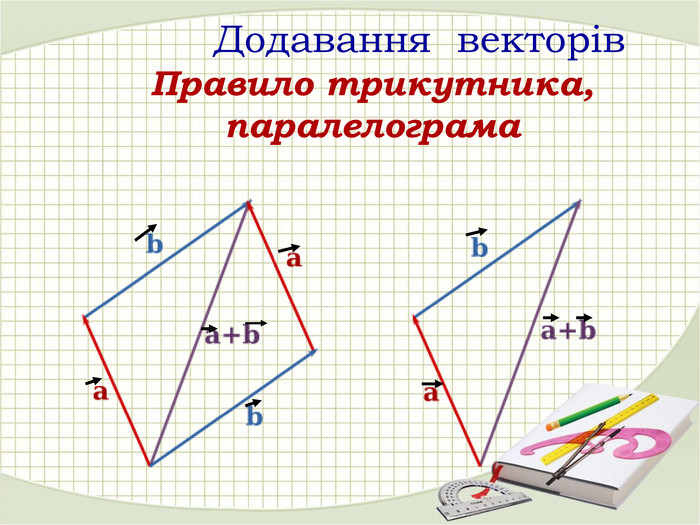
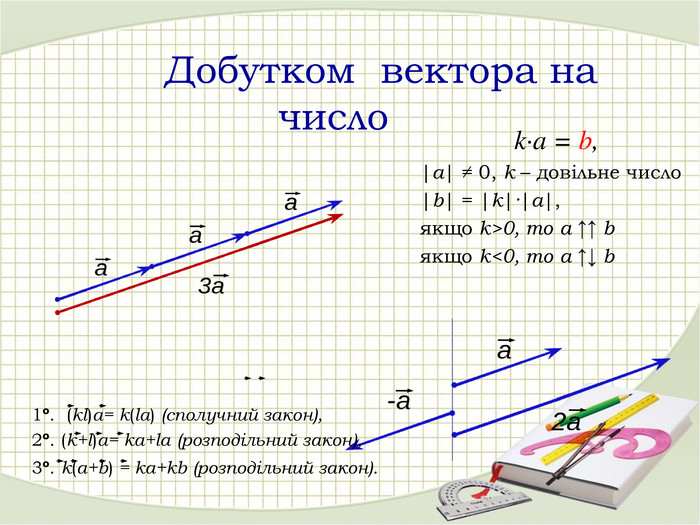
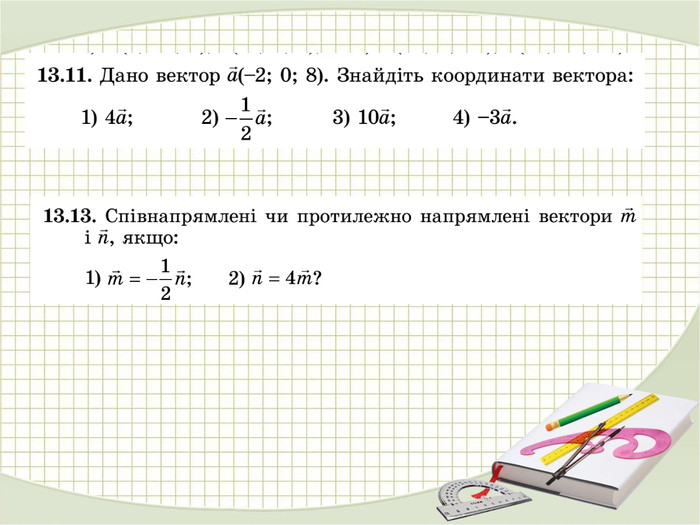
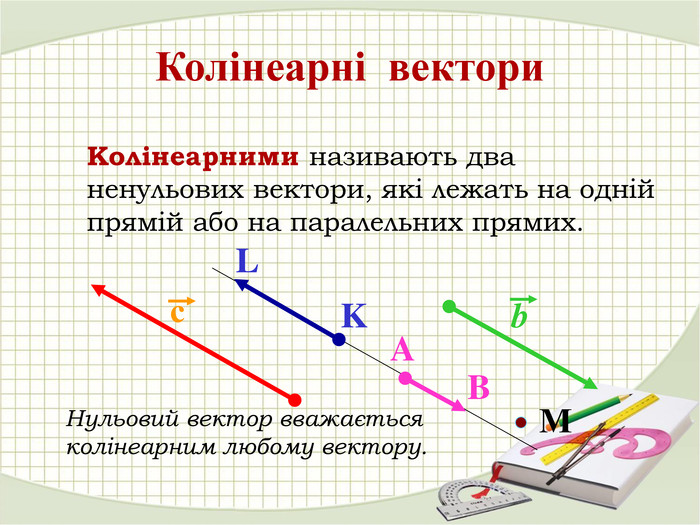
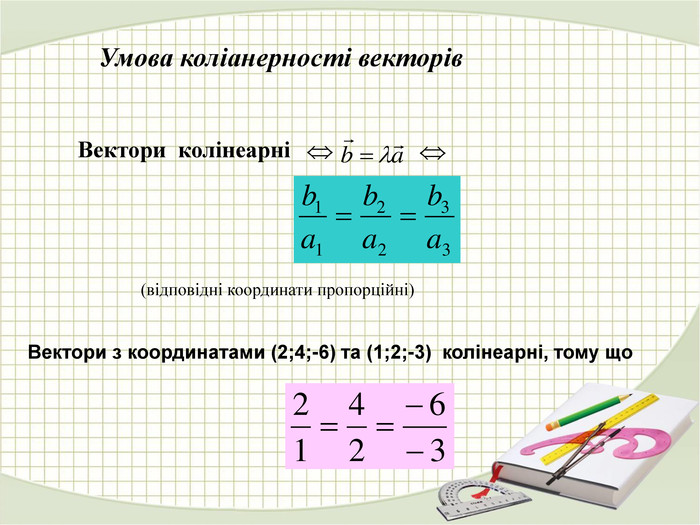
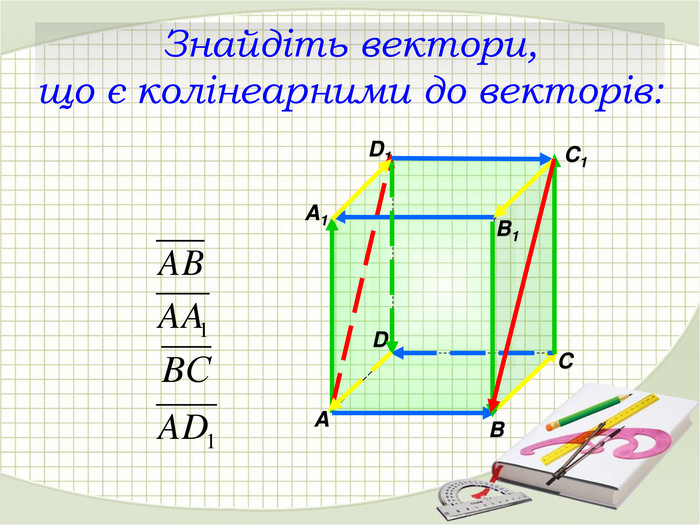
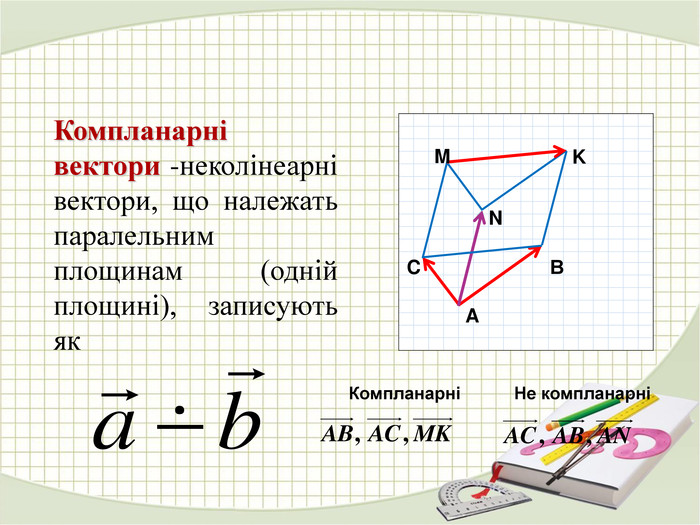
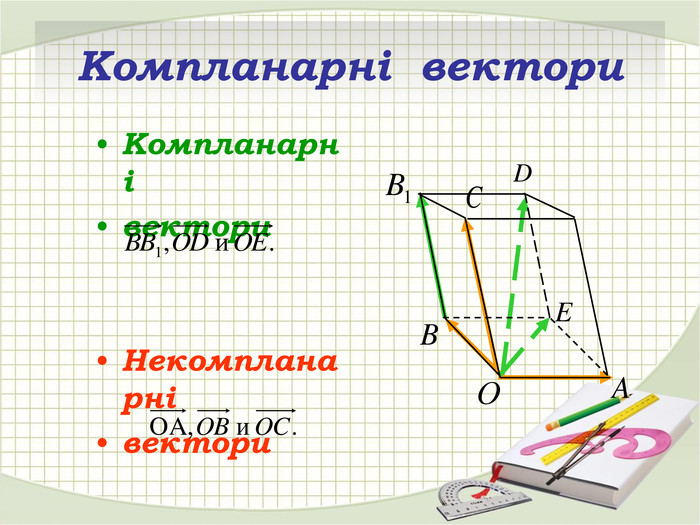
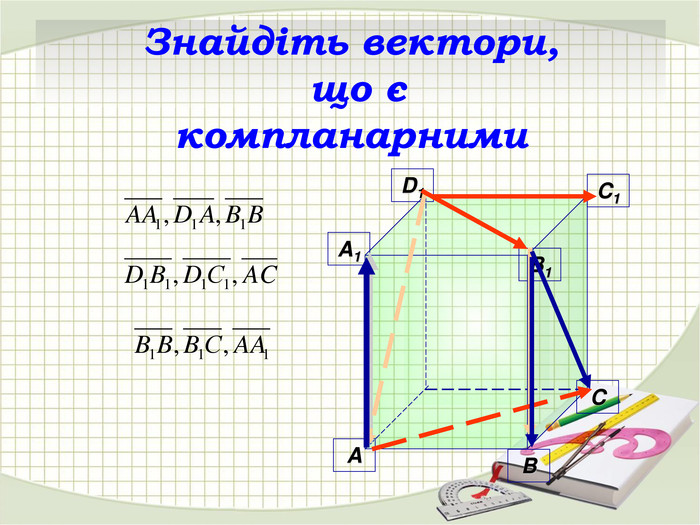
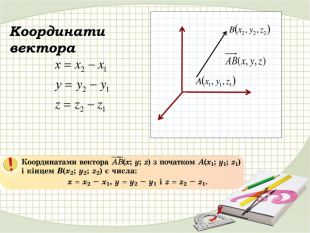
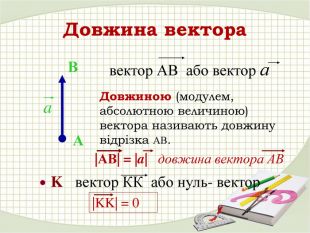
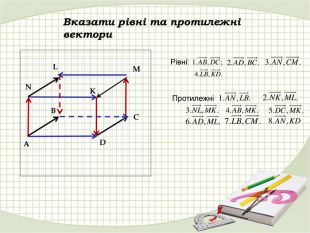
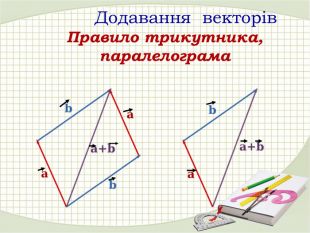
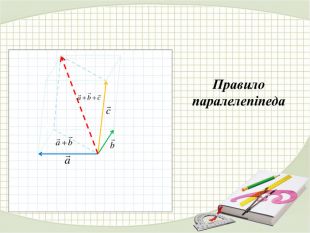
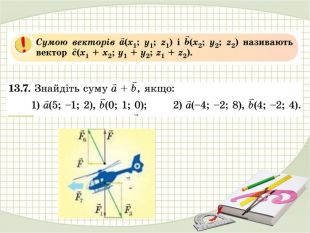
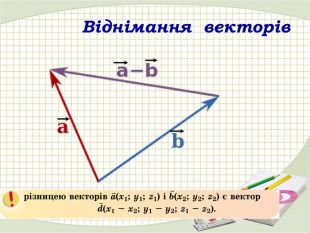
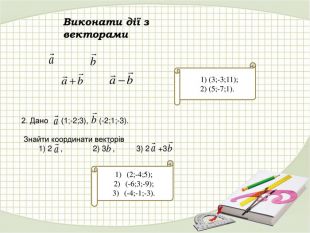
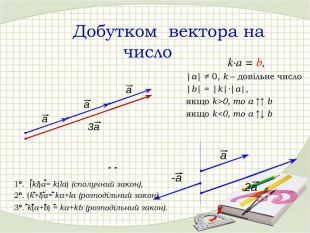
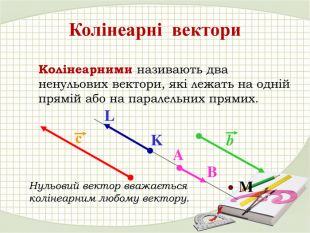
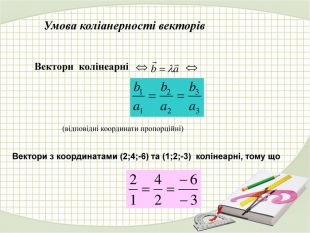
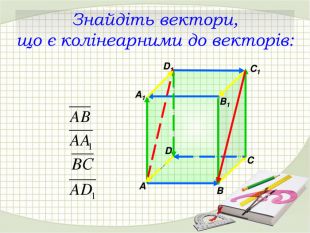
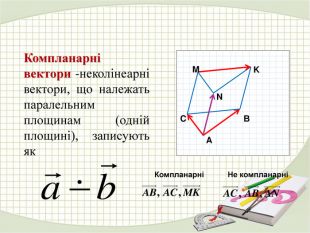
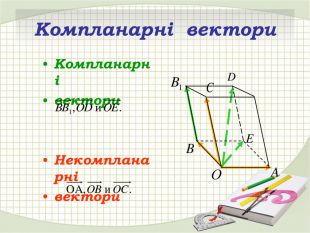
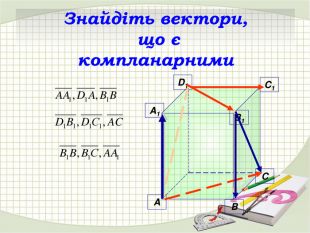
Презентація "Координати вектора. Дії над векторами, які задано координатами."
Про матеріал
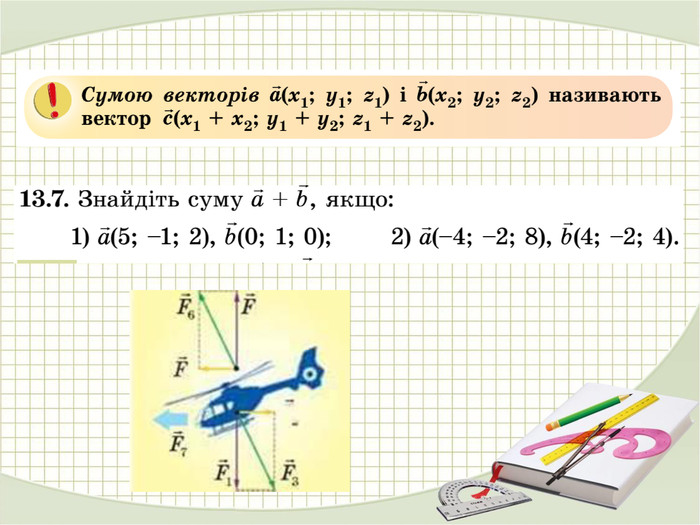
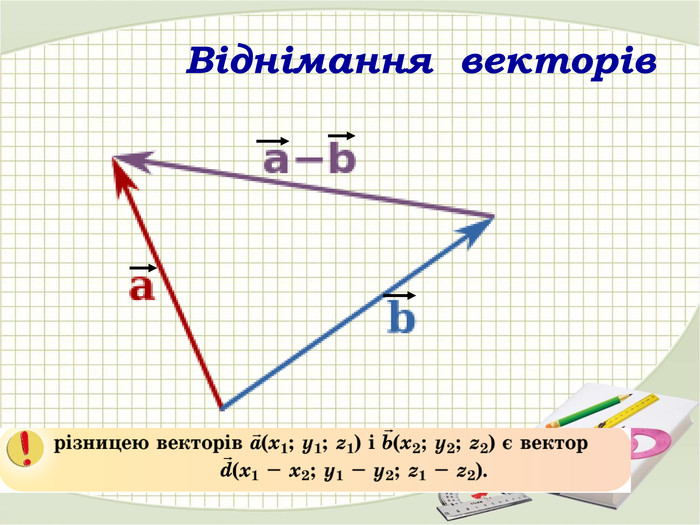
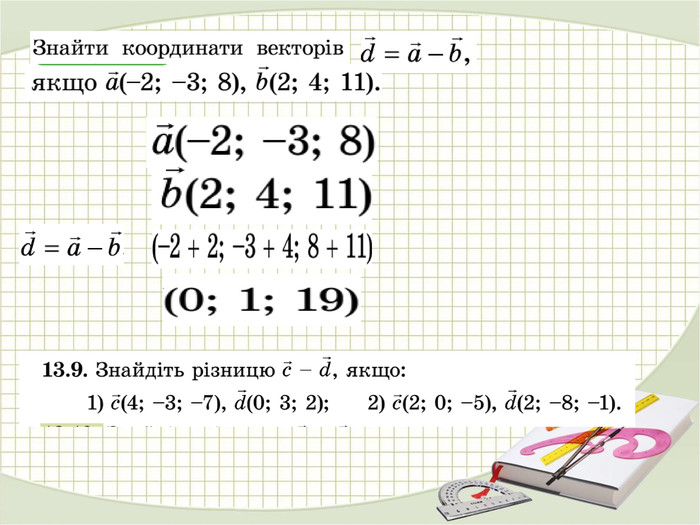
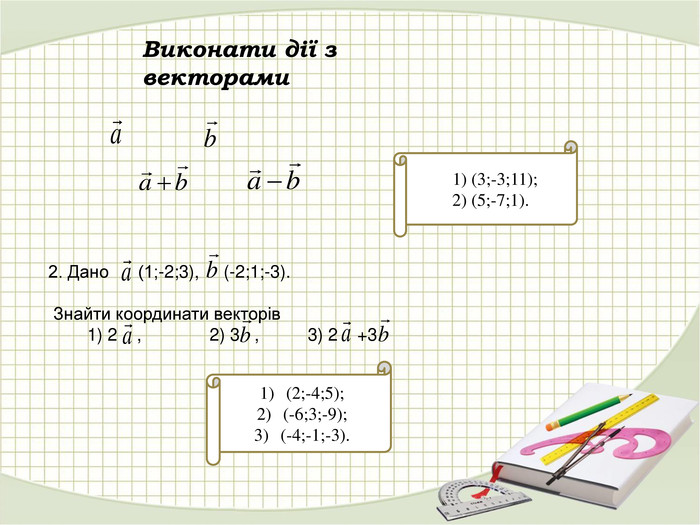
Матеріали презентації "Координати вектора. Дії над векторами, які задано координатами." приведені у відповідність до п. 13. підручника "Математика. Алгебра і початки аналізу та геометрія. 10 клас. Рівень стандарту." ( О. С. Істер). Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку