Презентація. Лінійна функція

Лінійна функція, пряма пропорційність у курсі математики основної школи

Мета: Сформулювати означення лінійної функції та прямої пропорційності, графіка лінійної функції, області визначення та області значення функції; Навчити учнів розрізняти функціональні залежності, лінійні функції; Навчити учнів будувати графіки лінійних функцій та розв’язувати задачі за допомогою графіків; Формувати вміння учнів використовувати знання про лінійну функцію, пряму пропорційність, графік лінійної функції під час розв’язування задач , показати практичне застосування лінійної функції в різних галузях.

х Приклад 1 Периметр квадрата у зі стороною х знаходиться за формулою у = 4х Fтяж Приклад 2 Сила тяжіння, що діє на тіло, прямо пропорційна масі тіла m , визначається за формулою: де - коефіцієнт, який у фізиці називається прискоренням вільного падіння Мотивація вивчення теми: при вивченні інших предметів ми часто маємо справу з лінійними функціями.

Лінійна функція Графік лінійної функції Пряма пропорційність Незалежна змінна (аргумент) Множина значень Область визначення Залежна Змінна (функція) Кутовий коефіцієнт Основні поняття теми:

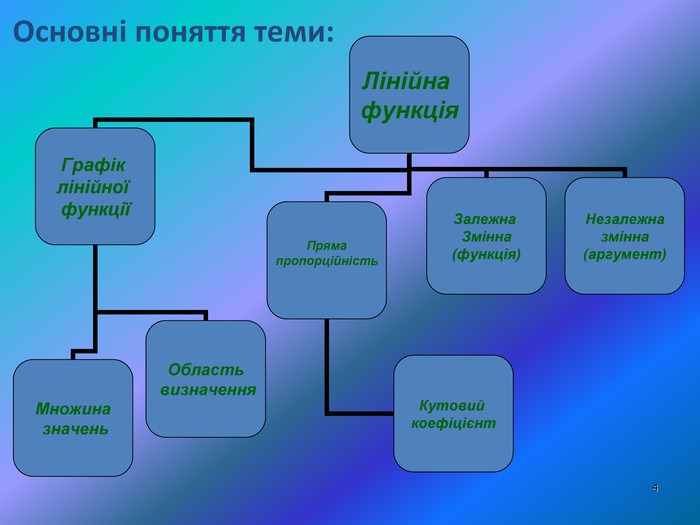
Лінійною функцією називається функція, яку можна задати формулою y=kx + b, де k і b – деякі числа, а x – незалежна змінна. у – залежна змінна (функція), х – незалежна змінна (аргумент). Графіком лінійної функції є пряма. Область визначень – множина всіх дійсних чисел. Множина значень – множина всіх дійсних чисел, якщо k≠0; якщо k=0, то число b. Функція y=kx при k≠0 називається прямою пропорційністю. k – кутовий коефіцієнт.

1) при b=0 (y=kx) – пряма, що проходить через початок координат; 2) при b≠0 (y=kx + b) – пряма, що не проходить через початок координат (яку отримали з прямої y=kx за допомогою паралельного перенесення вздовж осі Оу на b одиниць). 5. Графіком лінійної функції є пряма. k – кутовий коефіцієнт прямої 1) при k>0 функція зростає на всій області визначення; 2) при k<0 функція спадає на всій області визначення; 3) при k=0 функція стала. 4. Зростання і спадання 1) при k≠0, у=0 – точка перетину з віссю Ох; 2) k=0, тоді у= b – пряма, паралельна осі Ох перетинає Оу в точці (0; b) і збігається з віссю Ох при b=0; 3) у=b, х=0 – точка перетину з віссю Оу, тобто (0; b) . 3. Точки перетину з осями координат 1) при k≠0; у – будь-яке дійсне число; 2) при k=0; у=b. 2. Множина значень х – будь-яке дійсне число . 1. Область визначення Значення змінних Властивості Лінійною функцією називається функція, яку можна задати формулою y=kx + b, де k і b – деякі числа, а x – незалежна змінна.

Учень повинен: Наводити приклади функціональних залежностей, лінійних функцій; Пояснювати поняття: область визначення функції, область значення функції, графік функції; Формулювати означення понять: функція, лінійна функція, пряма пропорційність; Називати і характеризувати способи задання функції; Описувати побудову графіка функції, заданої таблично або аналітично; Розв’язувати вправи, що передбачають: - знаходження області визначення функції; - знаходження значення функції за даним значення аргументу; - побудову графіка лінійної функції; - з’ясування окремих характеристик функції за її графіком (додатні значення, від’ємні значення, нулі).

Кросворд Незалежна змінна. Початок координат. Фігура, яка задається двома координатами. Вісь Ох. Наочне зображення залежності. Графік лінійної функції. Ф Г А Ч А Я К А А У Ь А Т У Н К Ц І Р Г М Е Н Л Т О Б С И С Р А Ф П Р М Методичні прийоми

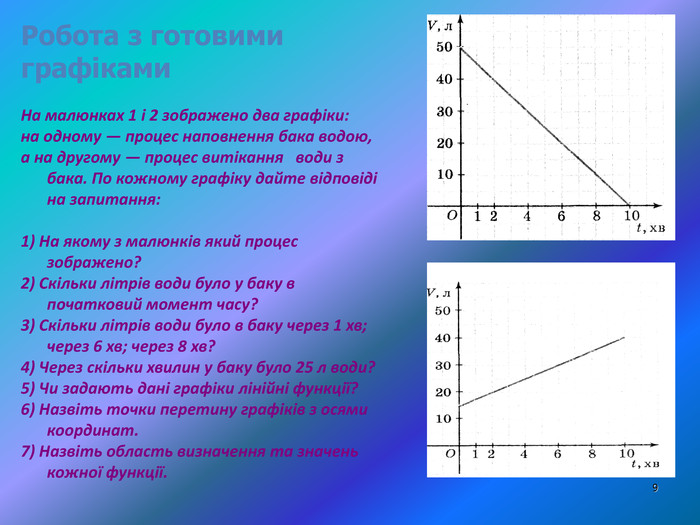
Робота з готовими графіками На малюнках 1 і 2 зображено два графіки: на одному — процес наповнення бака водою, а на другому — процес витікання води з бака. По кожному графіку дайте відповіді на запитання: 1) На якому з малюнків який процес зображено? 2) Скільки літрів води було у баку в початковий момент часу? 3) Скільки літрів води було в баку через 1 хв; через 6 хв; через 8 хв? 4) Через скільки хвилин у баку було 25 л води? 5) Чи задають дані графіки лінійні функції? 6) Назвіть точки перетину графіків з осями координат. 7) Назвіть область визначення та значень кожної функції.

Основні базові задачі Дано функцію. Знайти значення функції за заданим аргументом; значення аргументу, що відповідає значенню функції. Побудувати графік даної функції. Не виконуючи побудову, визначити, графіку якої з даних функцій належить дана точка. З поданих функцій вибрати зростаючі і спадні. Не виконуючи побудову, знайти координати точок перетину графіка даної функції з осями координат. Не виконуючи побудову, знайти координати точки перетину графіків функцій. Задати формулою лінійну функцію, графік якої проходить через дані точки. Виразити формулою залежність змінної х від змінної у, якщо залежність змінної у від змінної х виражається даною формулою.

Приклад 2: Побудувати графіки даних функцій в одній системі координат і записати координати точки їх перетину: у=-2х+1 і у=х-2. Розв’язання: 4х-3=2х+12; 4х-2х=12+3; 2х=15; х=7,5; у=2∙7,5+12=27; Точка перетину графіків – (7,5;27). Побудова: у=-2х+1; х=0, у=-2∙0+1=1; А(0;1); х=2, у=-2∙2+1=-3; В(2;-3); у=х-2; х=0, у=0-2=-2; С(0;-2); х=2, у=2-2=0; Д(2;0). Е(1;-1) – точка перетину. Приклад 1: Не виконуючи побудову, знайти координати точки перетину графіків функцій: у=4х-3 і у=2х+12.

Розв’язати задачу: Автомобіль, рухаючись зі швидкістю 72 км/год, проходить за t годин відстань S км. Виразити формулою залежність S від t. Побудувати графік функції: А) у=2х; Б) у=6; В) у=4х+1; Г) у=-4х+1; Д) у=-6. Не виконуючи побудови графіка, знайти координати точок перетину з осями координат графіка функції: А) у=9-3х; Б) у=5х+2; В) у=-х+6; Г) у=2х+4. Знайти координати точок перетину графіків функції: А) у=2х+1 та у=7х-9; Б) у=-3х+6 та у=5х-2; В) у=4х+3 та у=3х-5. Задачі

Написати рівняння прямої, яка проходить через точку А(х;у) і паралельна заданій прямій: А) А(2;11) у=-4х-1; Б) А(2;5) у=2х-1; В) А(1;4) у=2х. Графік лінійної функції у=kx+b перетинає осі координат в точках А і В, які задані своїми координатами. Знайти k і b. А) А(2;0) В(0;2); Б) А(1;0) В(0;-1); В) А(-1;0) В(0;3). Розв’язати задачу: Сплав складається з трьох металів, вміст яких в ньому пропорційний числам 10,6; 14; 25,4. Скільки кожного металу міститься в 96 кг сплаву? Побудувати графік функції у=-7х. Знайти за графіком: А) значення у, відповідне х, який дорівнює -1;0;1,5. Б) значення х, при якому значення у дорівнює -5;2;5. В) множину значень х, при яких значення змінної у додатні, від’ємні.

Тема: Лінійна функція та її графік Мета: сформувати свідоме розуміння учнями взаємозв'язку між вза­ємним розташуванням графіків двох лінійних функцій та співвідношенням їх кутових коефіцієнтів; виробити вміння: за даними рівняннями лінійних функцій робити висновки щодо взаємного розташування графіків; знаходити аналітичним способом координати точки перетину графіків двох лінійних функцій. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент Перевірка готовності учнів до уроку. Учні-консультанти повідомляють про стан виконання домашнього завдання. II. Перевірка домашнього завдання (зібрати зошити) Бліцтест Яка з формул задає лінійну функцію: 1) у = 7х – 0,5; 2) ; 3) ; 4) у = 7х; 5) у = 7х2 + 2. Варіанти відповіді: А. 1; 2; 3; 4. Б. 1; 3; 4. В. 1; 3; 4; 5. Г. Усі. Графік лінійної функції проходить через точку (0; 0) та точку . Задайте її формулою. Варіанти відповіді: А. у = -27х. Б. у = 27х. В. у = 3х. Г. у = -3х. Яким з рівнянь може бути задана лінійна функція, графік якої зображено на рисунку: Варіанти відповідіі: А. у = х - 2. Б. у = х + 2. В. у = 2х. Г. у = 2. В яких точках перетинає графік у = х – 7: а) вісь Оу; б) вісь Ох? Варіанти відповіді: A. а) (0; 7); б) (7; 0). Б. а) (0; -7); б) (-7; 0). B. а) (0; 7); б) (-7; 0). Г. а) (0; -7); б) (7; 0). Фрагмент уроку на тему “Лінійна функція та її графік”

III. Робота з випереджальним домашнім завданням Організуємо так: 1) перевіряємо, які графіки побудували учні (учні «презентують» свої роботи; коригують їх); 2) за алгоритмом порівняння здійснюємо порівняння ( а) формул, б) графіків ) та робимо висновки щодо виконаних завдань та формулюємо загальну гіпотезу. IV. Формулювання мети й завдань уроку Учитель разом з учнями формулює навчальну мету уроку (див. мета). V. Актуалізація опорних знань Виконання усних вправ Розв'яжіть рівняння: 1 + x = 1 - х; 9х – 4 = 9x + 5; 3x + 1 = 1,5 – х. Що можна сказати про прямі т і п (див. рис), якщо кути α і β: а) рівні; б) нерівні? Чи проходить графік функції у = -0,25х + 4 та у = х – 1 через точку А(4; 3)? Що можна сказати про взаємне розташування цих графіків? VI. Вивчення нового матеріалу Основну мету уроку — формування свідомого розуміння змісту взаємозв'язку між співвідношенням коефіцієнтів k1 і k2 у рівняннях лінійних функцій y = k1x + b1 та y = k2x + b2, ми проводимо індуктивним методом (випереджальне домашнє завдання тому підтвердження), тому ця частина зводиться до перекладу висновків, здобутих під час перевірки виконання домашнього завдання математичною мовою, а саме: 1) якщо лінійні функції y = k1x + b1 та y = k2x + b2 мають k1 = k2,а b1 ≠ b2, то графіки цих лінійних функцій паралельні; 2) якщо в рівняннях y = k1x + b1 та y = k2x + b2, що задають лінійні функції k1 ≠ k2, то графіки таких лінійних функцій перетинаються. Єдине, на що треба звернути увагу — як знайти точку перетину гра­фіків двох лінійних функцій. Для усвідомлення відповідного алгоритму, проведемо бесіду за планом: 1) Що означає вислів «Дві прямі перетинаються»? Що можна сказати про точку перетину? 2) Якщо y = k1x + b1 —лінійна функція і координати точки А(хА; уА) перетворюють це рівняння на правильну рівність, що це означає? А якщо координати цієї ж самої точки перетворюють рівняння y = k2x + b2 на правильну рівність, що це означає? 3) Точка А(хА; уА ) належить графікам y = k1x + b1 та y = k2x + b2. Яких значень будуть набувати вирази (k1x+b1) та (k2x+b2), якщо х = хА? 4) Відомо, що y = k1x + b1 та y = k2x + b2 — лінійні функції, графіки яких перетинаються в даній точці. Яких значень набувають ці функції при значенні аргументу, що дорівнює абсцисі цієї точки? Як це записати мовою математики? Після такої бесіди більшість учнів усвідомлює зміст переходу від геометрично заданих функцій (функції як прямі) до аналітичного змісту умови перетину їх графіків. Результати обговорення бажано записати в зошити.

VI. Первинне закріплення знань. Вироблення вмінь Виконання усних вправ Чи перетинаються графіки функцій? Чому? 1) у = 8х – 11; у = 5х – 10; 2) у = 8х – 11; у = 5х – 11; 3) у = 8х – 11; у = 8х – 10; 4) у = 8х; у = -8х. Серед функцій: у = x + 0,5; у = -0,5х + 4; y = 5x – 1; y = 0,5x + 1; виділіть ті, графіки яких паралельні графіку функції у = 0,5х + 4. Яка лінійна функція має графік, що паралельний до графіка функції у = 1,3х – 7 і проходить через початок координат? Виконання письмових вправ Знайдіть координати точок перетину графіків функцій: 1) у = 10х – 8; та у = -3х + 5; 2) у = 14 – 2,5х та у = 1,5х – 18; 3) у = 20х – 70 та у = 70х + 30; 4) у = 37х – 8 та у = 25х + 4; 5) у = 14х та у = х + 26; 6) у = -5х + 16 та у = -6. Дано лінійну функцію .у = 2,5х+4. Задайте формулою таку лінійну функцію, щоб її графік: 1) був паралельний до графіка цієї функції; 2) перетинав графік цієї функції і проходив через початок координат; перетинав графік цієї функції в точці перетину даного графіка з віссю Оу. Покажіть схематично взаємне розташування на координатній площині графіків функцій: у = 17х та у = 17х – 20; у = -30х та у = -30х + 8; 3) у = 3х – 2 та у = -3х – 2. VII. Підсумок уроку («Аукціон» або вікторина) На рисунку зображено графіки 2-х лінійних функцій (І, II). Які висновки щодо k та b ви можете зробити? VIII. Домашнє завдання № 1. Повторіть зміст основних понять теми (див. конспект). Складіть питання до вікторини за темою «Функція». № 2. Чи перетинаються графіки функцій: 1) у = 6х + 9 та у = 2х – 7; 2) у = -0,5х + 2 та у = 2,5х – 10; 3) у = 0,2х – 9 та у = х + 1; 4) у = х та у = -3х + 3,4? Для графіків, що перетинаються, знайдіть координати точки перетину. № 3. Задайте формулою лінійну функцію, графіком якої є пряма, що проходить через точку А (2; 3) і паралельна до графіка функції у = 1,5х – 3. Побудуйте її графік.

1м тканини коштує 120:5=24 грн у=24х х=2,5 => у=60 2,5 м тканини коштує 60 грн Прикладні задачі Задача1. Побудувати графік залежності вартості тканини (в гривнях) від її кількості (в метрах), знаючи, що 5 м тканини коштують 120 грн. Визначити за графіком, скільки коштує 2,5 м тканини?

Задача2. Шнур розрізали на три частини, довжини яких пропорційні числам 5,7,13, причому довжина більшого відрізка шнура перевищує довжину меншого на 2,88 см. Знайти довжину кожної частини шнура. а:в:с як 5х:7х:13х с-а=2,88 13х-5х=2,88 8х=2,88 х=0,36 а=5*0,36=1,8 в=7*0,36=2,52 с=13*0,36=4,68

В-2 9 балів 7 балів В-2 В(2;-16) А(-0,5;4) В(-11;22) А(1,5;-3) 3. Графік прямої пропорційності проходить через точку В, чи проходить цей графік через точку А, якщо: у=1/5х-2/7 у=3/8-2/3х 2. Знайти координати точок перетину графіка функції з осями координат у=5-0,2(х-4) у=7-0,5(х+1) 1. Побудувати графік функції 12 балів В-1 D(7;21) С(40;-20) В(-40;-40) А(400;200) Чи належить цьому графіку точка? у=0,3х у=-Ѕх у=-х у=2х 3. Побудувати графік функції у=2(х+3)-5 та у=3х-8 у=3(х-1)+2 та у=-3х-1 у=6х-11 та у=8-10х у=-х+4 та у=4х-8 2. Не виконуючи побудови графіків функцій, знайти координати точок їх перетину у=7-2х у=-4х+6 у=х+3 у=2х-1 1. Побудувати графік функції В-2 В-1 В-1 Самостійна робота. Лінійна функція. Пряма пропорційність

Математичний диктант Назвіть кутовий коефіцієнт функції у=-2х+3. Скільки точок графіка лінійної функції потрібно знайти, щоб побудувати її графік? Гострий, тупий чи прямий кут утворює графік функції у=3х-1 з додатним напрямком осі Ох? Функція задана формулою у=2х-6 . Чи проходить графік цієї функції через точку А (2; -2)? Знайдіть значення функції у=4-3х, якщо значення аргументу дорівнює -1 ? Знайдіть нулі функції у=15-3х.