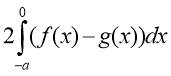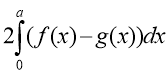знаходження площі плоскої фігури за допомогою інтеграла
Тема. Обчислення площі плоскої фігури за допомогою інтеграла.
Мета.
навчальна: формувати в учнів вміння застосовувати інтеграл до знаходження площ плоских фігур;
розвиваюча: розвивати логічне мислення, пам'ять, увагу, математичну грамотність, уміння лаконічно й чітко формулювати думку.
виховна: виховувати акуратність, наполегливість, толерантність, інтерес до вивчення математики.
Тип уроку: формування вмінь і навичок.
Обладнання та наочність: презентація « Обчислення площ плоских фігур»,
Хід уроку.
І. РОЗМИНКА.
Переконана, що для кожнонг, хто тут присутній, незаперечним фактом є те, що для пізнання нового використовують відомості, уміння, навички попередні. А в математиці – особливо. Тому пропоную пригадати терміни, поняття, що згадувались на попередніх уроках, за допомогою ХМАРИ СЛІВ, яку ви маєте завантажено на ваших гаджетах. (Учні називають і коментують). - Чи є серед даних понять те, що ми ще не згадували?(площа плоскої фігури)
Так дійсно, саме з цим поняттям ми сьогодні ознайомимось.
Запишемо тему: Знаходження площі плоскої фігури, обмеженої лініями, за допомогою інтеграла
І пропоную спочатку розглянути ваше домашнє завдання.
В домашньому завданні вам потрібно було знайти площі деяких фігур.
Д/З. перевірка (слайд 1)
На рис. зображено графіки функцій ![]() (пряма РК) і х = - 3 (пряма РМ). Установіть відповідність між фігурами (1-4) і числовими значеннями їх площ (А-Д).
(пряма РК) і х = - 3 (пряма РМ). Установіть відповідність між фігурами (1-4) і числовими значеннями їх площ (А-Д). 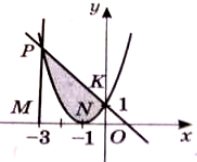
- МРКО А. 4
- NOK Б. 4,5
-
MNP B.
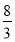
-
PKN (затушована) Г.
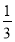
Д. 7,5
Запитання до класу:
- Чи усі фігури є криволінійними трапеціями? ( остання ні)
- Як ви знайшли площу зафарбованої фігури? (як різницю між першою і сумою другої і третьої)
- Чи не задовгий шлях?
- Чим обмежена дана фігура? Чи замітили ви різницю між криволінійною трапецією і фігурою , що не нею?
ІІ. ОБГРУНТУВАННЯ НАВЧАННЯ
Давайте розглянемо подібні фігури у загальному вигляді і спробуємо скласти формулу для знаходження її площі, використовуючи відомі нам знання – площу криволінійної трапеції.
(слайд 2)
Запитання
- Що спільного у всіх малюнках? Що відмінного?
А) 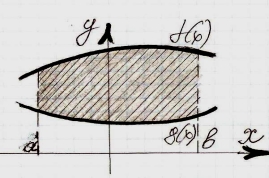 Б)
Б) 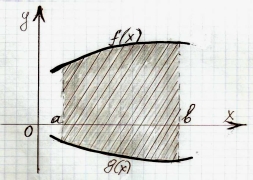
В) 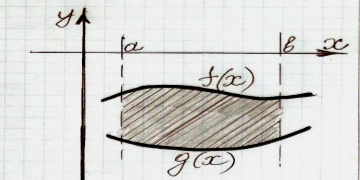
А) S=Sf-Sg = 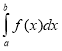 --
-- 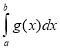 =
=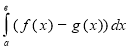
Б) S=Sf+Sg = 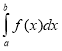 + (-
+ (-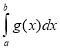 ) =
) = 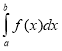 -
- 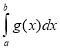 =
=![]()
В) S=Sg-Sf =(-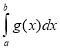 ) – (-
) – (-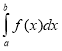 ) =
) = 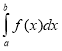 -
- 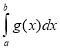 =
=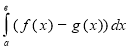
Отже, формула S= дає можливість знаходити площі
дає можливість знаходити площі
плоских фігур, що не є криволінійними трапеціями і обмежені лініями, за допомогою інтеграла.
 І давайте повернемось до домашнього завдання. Знайдемо площу замальованої фігури за отриманою формулою.( слайд 3) На рис. зображено графіки функцій
І давайте повернемось до домашнього завдання. Знайдемо площу замальованої фігури за отриманою формулою.( слайд 3) На рис. зображено графіки функцій ![]() (пряма РК) і х = - 3 (пряма РМ).
(пряма РК) і х = - 3 (пряма РМ).
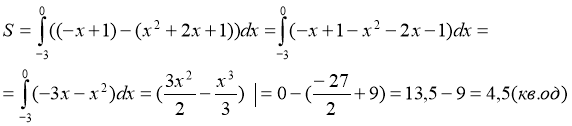
![]()
ІІІ. УСВІДОМЛЕННЯ ЗМІСТУ.
ЗАВДАННЯ 1.
(Слайд 4). Записати формулу знаходження площі зафарбованої фігури.
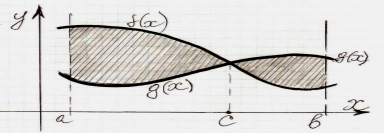
Запитання до класу:
- Як знайти значення с, якщо б не було задано?
- Як знайти точку перетину двох графіків функцій?
ЗАВДАННЯ 2.
(Слайд 5). Вибрати правильну відповідь

|
А |
Б |
В |
|
|
|
|
ЗАВДАННЯ 3.
 (Слайд 6). Знайти площу фігури, обмежену лініями
(Слайд 6). Знайти площу фігури, обмежену лініями ![]()
Запитання:
- де і яка функція зображена?
- Які межі інтегрування?
- Як знайти межі інтегрування? (прирівняти дві функції і розв’язати рівняння)
Учні знаходять межі, записують формулу для знаходження площі фігури і обчислюють інтеграл.
Сформулюємо алгоритм знаходження площі фігури, обмеженої лініями:
1.Знайти точки перетину графіків ( їх абсциси є межами інтегрування).
2. побудувати графіки даних функцій і замалювати фігуру.
3. знайти площу за допомогою інтеграла.
ЗАВДАННЯ 4. Підручник № 11.10 (11) авт.. Мерзляк, Полонський
Знайти площу фігури, обмеженої лініями у=х2 і у=х3.
ПІДСУМОК.
З чим ознайомились?
Що вчились робити?
Що склали? (алгоритм)
Прошу прорангувати складність виконання кроків алгоритму по складності саме для вас. (проговорюємо найважчий крок)
Д / З. Розв’язати № 11.10 (1,2), виконати вправу за посиланням
Повернемось до слів В. Кілпатріка
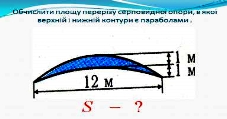
Поставимо перед собою завдання розв’язати задачу практичного характеру: Обчислити площу перерізу серповидної опори, в якої верхній і нижній контури є параболами. Серповидна опора задовольняє початковим умовам: (слайд 10)
Розв'язання

1. Перенесемо рисунок задачі в декартову систему координат (слайд 11)
2. Згідно умови переріз опори є параболічний сегмент. Отже потрібно задати формули парабол, які обмежують даний сегмент: (слайд 12)
![]() - загальний вигляд контурів опори. Причому, використовуючи теорію перетворення та умову задачі можемо записати, що рівняння набуває вигляду
- загальний вигляд контурів опори. Причому, використовуючи теорію перетворення та умову задачі можемо записати, що рівняння набуває вигляду ![]() ,
, ![]() Залишається знайти значення коефіцієнта аi: за побудовою графіки проходить через точку
Залишається знайти значення коефіцієнта аi: за побудовою графіки проходить через точку ![]() . Отже, координати цієї точки повинні задовольняти рівнянням обох парабол: Знайдемо рівняння, яке задає нижній контур:
. Отже, координати цієї точки повинні задовольняти рівнянням обох парабол: Знайдемо рівняння, яке задає нижній контур: ![]() . Отже нижня опора задається рівнянням
. Отже нижня опора задається рівнянням ![]() .
.
- Знайдемо рівняння верхньої опори.
![]() . Отримали, що верхня опора задається рівнянням:
. Отримали, що верхня опора задається рівнянням: ![]()
- Чи є побудована фігура криволінійною трапецією? ( Відповідь: ні)
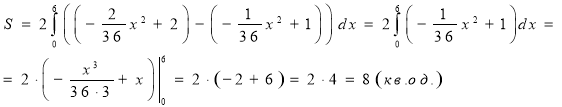
КОМЕНТАР. Від площі перерізу опори звичайно залежить міцність опори, площа опори впливає на її об’єм , а об’єм такої фігури також знаходиться за допомого інтеграла. Але про це ми поговоримо на наступних уроках.
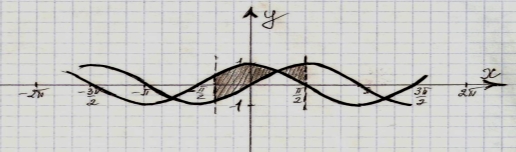
(Слайд 14). Записати формулу площі зафарбованої фігури та знайти площу.
1


про публікацію авторської розробки
Додати розробку