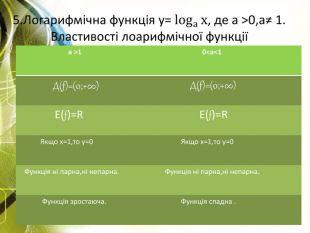
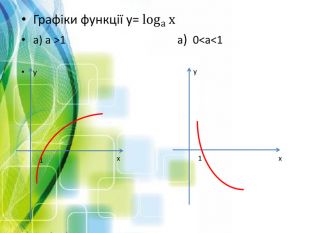
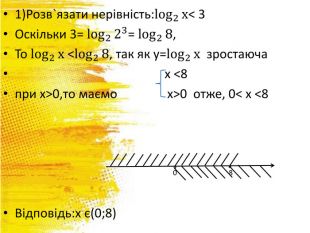
Презентація Логарифмічна функція
Про матеріал
Зміст презентації складається із теоретичної частини та розв'язку логарифмічних рівнянь та нерівностей. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку







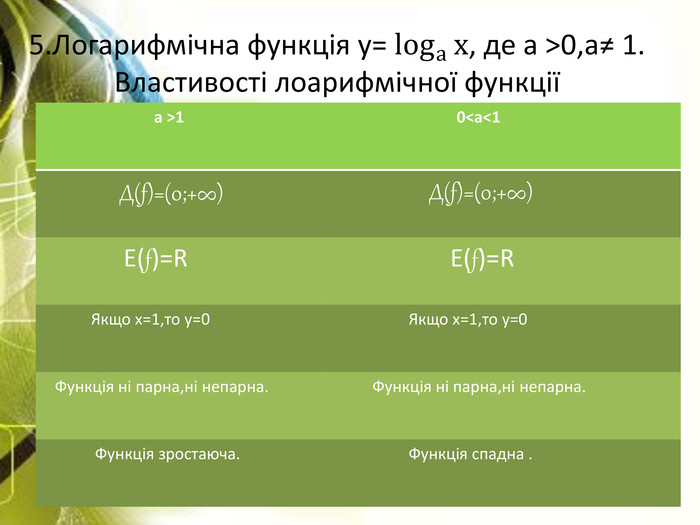









![3)Розв`язати нерівність графічно:log3х≤4-х. Будуємо графіки функцій у= log3х і у=4-х в одній системі координат. Графіки перетинаються в точці з абцисою х=3. Із рисунку видно,що множина розв`язків нерівності log3х≤4-х є проміжок (0;3]Відповідь:х є(0;3] ух3401 3)Розв`язати нерівність графічно:log3х≤4-х. Будуємо графіки функцій у= log3х і у=4-х в одній системі координат. Графіки перетинаються в точці з абцисою х=3. Із рисунку видно,що множина розв`язків нерівності log3х≤4-х є проміжок (0;3]Відповідь:х є(0;3] ух3401](/uploads/files/461847/112283/119831_images/18.jpg)