Презентація "Логарифмічні рівняння з параметром"
Про матеріал
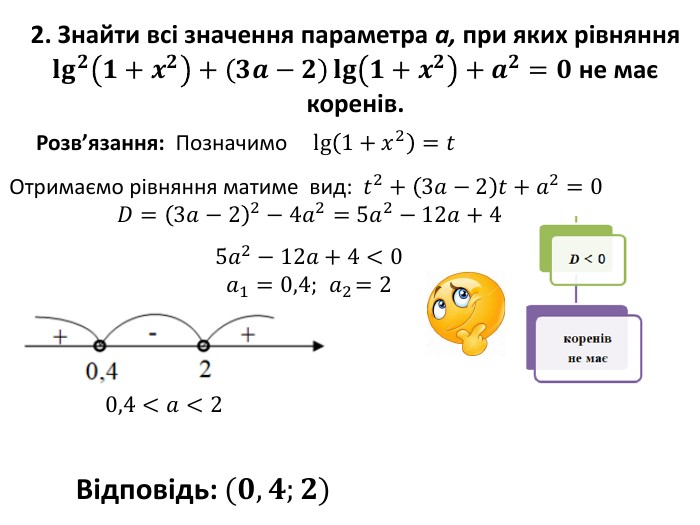
Презентація "Логарифмічні рівняння з параметром" за допомогою цього матеріалу можна підготувати дітей до НМТ та ЗНО. У даній презентації містяться рівняння різної складності з параметрами з розв'язком для зручності пояснення матеріалу Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку