Презентація "Математика в професійній діяльності кравців"

Кравець. Закрійник.

Задачі: Дві диванні подушки-валики одягаються в чохли. Довжина 1 валика в 2 рази більше другого, але радіус його основи вдвічі менше другого. На який чохол пішло більше тканини? У швацьку майстерню надали заказ на виготовлення чохлів до диванних валиків, довжина валика 80 см, а діаметр 24 см. Скільки квадратних метрів меблевої тканини потрібно для пошиву 10 чохлів, якщо на за­лишки від крою відходить 15% тканини? Знайти висоту та радіус циліндричної частини капелюха, який має найбільшу площу бокової поверхні, якщо периметр осьового перерізу дорівнює 2 р. Скільки шкіри піде на покриття футбольного м'яча радіусом 10 см? (На шви додати 8% від площі поверхні м'яча)Із прямокутного шматка тканини розміром 5 дм х 8 дм потрібно зшити косметичку найбільшого об'єму. Якої довжини повинна бути сторона квадратних куточків на викройці?

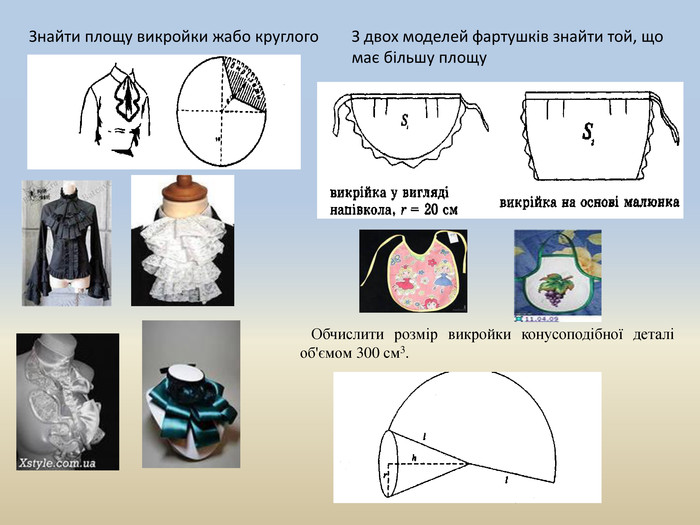
Які основні варіанти прямого силуету ви можете виділити з умовою їх подібності з геометричними фігурами?Відповідь: конструкція виробів із квадратною проймою;силует у вигляді трапеції, що припускає розширену лінію плеча і звужування форми донизу або навпаки: звужену лінію плеча і розширену форму донизу;конічна форма спідниць типу «сонце» і «напівсонце»; манжети, форми зрізаного конуса;прямокутник із різним ступенем свободи облягання. При розкрої спідниць типу «сонце» і «напівсонце» лишаються шматочки тканини у вигляді кола і на-півкола. Вирізати з них прямокутники максимальної площі для використання розкрою дрібних деталей прямокутної форми.

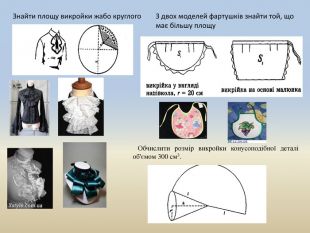
На малюнках костюми клоуна та сніговика. Завдання: Назвіть форму капелюшка. Зробіть малюнки викройок капелюха. Скільки квадратних метрів потрібно для пошиву капелюха карнавального костюма?Примітка: Для обчислення обрати розміри: розмір капелюха - 54 см; висота капелюха - 20 см; значення взяти за 3.

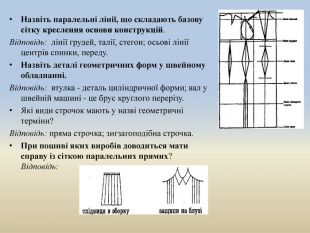
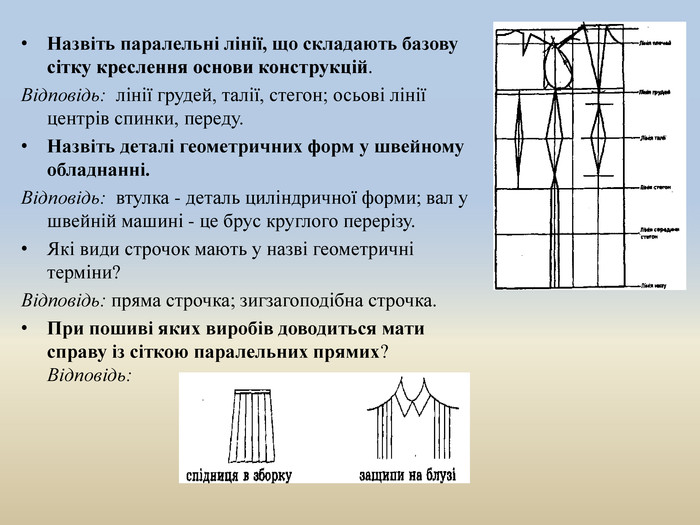
Назвіть паралельні лінії, що складають базову сітку креслення основи конструкцій. Відповідь: лінії грудей, талії, стегон; осьові лінії центрів спинки, переду. Назвіть деталі геометричних форм у швейному обладнанні. Відповідь: втулка - деталь циліндричної форми; вал у швейній машині - це брус круглого перерізу. Які види строчок мають у назві геометричні терміни?Відповідь: пряма строчка; зигзагоподібна строчка. При пошиві яких виробів доводиться мати справу із сіткою паралельних прямих?Відповідь:

Яку форму має прямий рукав у зшитому вигляді?Відповідь: циліндр, де окат рукава - переріз циліндра під кутом до основи. Назвіть вирізи горловин геометричної форми. Відповідь: У скільки квадратних метрів наметової тканини необхідно для пошиву намету діаметром основи 4 м і висотою 3,5 м? Відповідь. 25 м2. Які розрахунки необхідно знати для крою деталей сумки-боченка? Оберіть їх самі і знайдіть витрату тканини в кв. метрах. Потрібний чохол на подушку у вигляді півкулі об'ємом V. Визначте діаметр. На малярний валик діаметром 8 см і довжиною 25 см потрібно зшити шубку. Скільки потрібно тканини, якщо напуск на шов 1 см?

Знайти площу викройки жабо круглого. З двох моделей фартушків знайти той, що має більшу площу. Обчислити розмір викройки конусоподібної деталі об'ємом 300 см3.

ПРОБЛЕМНА ЗАДАЧА. У швейному цеху є в наявності 164 м тканини, з якої треба пошити халати та піжами. На пошиття халата витрачається 3 м тканини, а піжами -4 м. Скільки потрібно виготовити халатів і піжам для одержання найбільшого прибутку від їх реалізації, якщо вартість халата а гривень, а вартість піжами складається з добутку вартості халатів і їх кількості?І Дискусія до розв'язання задачі: Які змінні величини ми маємо? (Кількість піжам і халатів)Відокремте відомі дані з умови задачі. До чого зводиться розв'язання задачі?Найраціональніший варіант розв'язання.ІІ Розв'язання задачі . Відповідь. Піжам потрібно пошити 20, а халатів - 28. 

ЗАДАЧА: При розкроюванні залишалася тканина у формі ромбу з діагоналями 2а і 2 Ь, які можуть бути використані для розкрою дрібних деталей прямокутної форми. Знайти розміри прямокутника, вписаного в даний ромб так, що залишки від ромба будуть мінімальними. Дискусія до умови задачі:- Які дрібні деталі прямокутної форми може мати та чи інша модель?(Кишені, листочки, клапани, погони, хлястик, пати, манжети, невелика петля)- Яким передбачається бути прямокутник, щоб залишки від ромба були мінімальними?(Найбільшої площини)- Що необхідно скласти для вирішення задачі?(Функцію)- Який оптимальний вибір наданих для складання функції?- Назвіть варіанти планів наступної роботи для розв'язання задачі.- Назвіть формули площ ромба і прямокутника. Розв'язання задачі

В городе Бердичиве живет трое портных, и все на одной улице. У первого вывеска: “Лучший портной в городе”. У второго — “Лучший портной в мире”. У третьего — “Лучший портной на этой улице”. Все три вывески лгут. Вопрос: к кому лучше идти шить костюм?Задача - головоломка

Золотий переріз у дизайніДля дизайнерів одягу, найважливішим є розібрати пропорції фігури людини. Треба зауважити, людина здатна інтуїтивно відчувати пропорції золотого перерізу. Працюючи над картиною, вишивкою або костюмом, сам того не знаючи, дизайнер закладає золоті пропорції в свої творіння. Нічого дивного, адже золота пропорція у нас завжди перед очима, у вигляді самих себе.

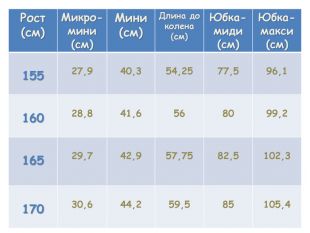
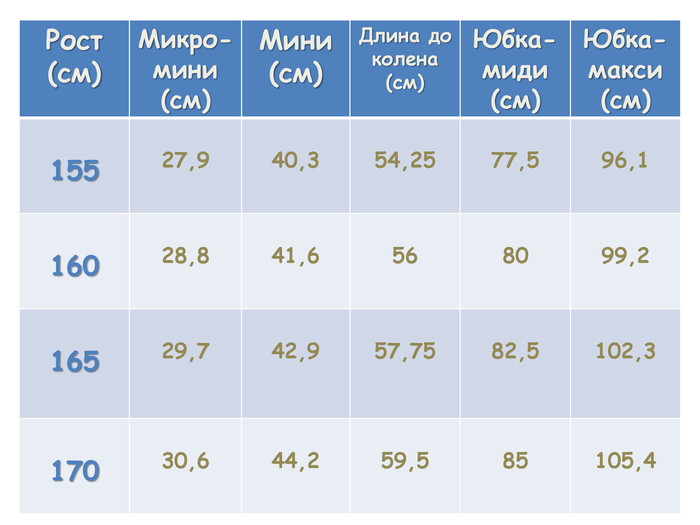
О выборе длины юбки. Длину юбки можно рассчитать по следующим формулам: Микро-мини: ДИ =  0,18 * Р Мини: ДИ =  0,26 * РГруппа мини-юбок довольна широка, поэтому выбор нужной длины можно делать в диапазоне - от 0,22 * Р до 0,3 * Р. Длина до колена: ДК = 0,35 * Р ДИ = ДК – 3 Юбка-миди: ДИ= 0,5 * РДлину "миди" можно выбирать из диапазона - от 0,4 * Р до 0,55 * РЮбка-макси: ДИ = 0,62 * РВсе приведенные выше формулы разработаны на основе Золотого сечения и позволяют создавать модели поясной группы, идеально подходящие любой девушке.*ДИ – длина изделия; ДК – уровень колена; Р - рост

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Рост(см)Микро-мини(см)Мини(см)Длина до колена(см)Юбка-миди(см)Юбка-макси(см)155 27,9 40,3 54,25 77,5 96,1 16028,8 41,6 56 80 99,2 16529,7 42,9 57,7582,5 102,3 17030,6 44,2 59,5 85 105,4

Функції в одязі

Геометрія ліній

Геометрія побуту

Промислова швейна машинка складається із головки машини, промислового стола, індивідуального приводу. Промисловий стіл (верхня частина) – це платформа, що має форму призми, стійка рукава - зрізана піраміда на призмі ( платформі), махове колесо кріпиться гвинтом на головному валу ( комбінації циліндра, зрізаного конуса, циліндра).

Деталі та механізми швейної машинки. Ви бачите різноманітні геометричні фігури - циліндри, конуси, призми. Комбінації цих геометричних фігур приводять у рух механізми швейної машини. Ці механізми – дві або більше з’єднаних між собою ланок, які не мають жорсткого скріплення і можуть здійснювати під дією прикладених сил цілеспрямовані рухи. Механізм приводить в дію основні робочі деталі машини – голку, човник, ниткопритягувач і т. д. Для перетворення обертового руху головного вала в поступальний рух застосовують кривошип, ексцентрики, шатуни, повзун, зубчасті шестерні, гвинти. В сукупності всі ці елементи є комбінаціями циліндрів, конусів, призм.

Механізм голки. Головний вал обертається у втулках. На правому кінці головного валу гвинтами закріплено махове колесо, на лівому кінці головного валу гвинтом закріплений кривошип з противагою. В отвір кривошипа вставлений подвійний палець, який закріплений гвинтами. На палець надіта верхня головка шатуна. В отвір нижньої головки шатуна вставлений палець, який лівою частиною спрямований до поводка голковода, а на праву частину цього пальця надітий повзун. Голковід переміщується у двох втулках. Внизу на голководі кріпиться дротяний нитконаправлювач, гвинтом у голководі закріплена голка. При обертанні головного валу кривошип і його подвійний палець з допомогою шатуна обертальний рух перетворюють у зворотно-поступальний рух голковода і голки.

1. Головний вал – циліндр.2. Кривошип – комбінація циліндра з призмою.3. Шатун – комбінації призм циліндра.4. Повзун – призма.5. Нижня головка шатуна, яка надіта на палець- комбінація циліндра іпризми.6. Поводок голковода – комбінація двох циліндрів і призми.7. Втулка – комбінація двох циліндрів.8. Гвинт кріплення – циліндр в комбінації з призмою.9. Втулка – комбінація циліндрів.10. Палець – призма у циліндрі.

ЗАДАЧІCкільки квадратних метрів наметової тканини необхідно для пошиву намету діаметром основи 4 м і висотою 3,5 м? Які розрахунки необхідно знати для крою деталей сумки - боченка? Оберіть їх самі і знайдіть витрату тканини в кв. метрах. Потрібний чохол на подушку у вигляді півкулі об'ємом V. Визначте діаметр. На малярний валик діаметром 8 см і довжиною 25 см потрібно зшити шубку. Скільки потрібно тканини, якщо напуск на шов 1 см?Розкрій елегантного модного пончо являє собою в основі 2 великих півкола. Скільки кв. м тканини потрібно у чистому вигляді на пончо довжи­ною 0,7 м? Припуск на підгин та шви - 5 см. На прямокутну нашивку спортивної куртки потрібно прикріпити лейбл такої ж форми, відступивши зверху і знизу нашивки по З см, а з боків по 2 см. Якими повинні бути найбільш вигідні розміри нашивки, якщо взяти до уваги економію тканини? Площа нашивки 150 см2

Тема: Похідна та її застосування. ПРОБЛЕМНА ЗАДАЧА. При розкроюванні залишалася тканина у формі ромбу з діагоналями 2а і 2 Ь, які можуть бути використані для розкрою дрібних деталей прямокутної форми. Знайти розміри прямокутника, вписаного в даний ромб так, що залишки від ромба будуть мінімальними. Дискусія до умови задачі: Які дрібні деталі прямокутної форми може мати та чи інша модель?(Кишені, листочки, клапани, погони, хлястик, пати, манжети, невелика петля) (Показ цих деталей на слайдах моделей). Яким передбачається бути прямокутник, щоб залишки від ромба були мінімальними? (Найбільшої площини)Що необхідно скласти для вирішення задачі?(Функцію)Який оптимальний вибір наданих для складання функції?Назвіть варіанти планів наступної роботи для розв'язання задачі. Назвіть формули площ ромба і прямокутника. Розв'язання задачі

Тема. Застосування похідної. Мета. Застосувати похідну для економічного розкрою тканини. Проблема. Які оптимальні розміри низу клина спідниці при заданій ширині тканини? Зміст роботи. Оформлення ескізу креслення. Виконання розрахунків. Моделювання клина спідниці. Виконання зарисовок моделей спідниць в клини. Запитання для підготовки до роботи: Яку кількість клинів може мати спідниця? (4, 5, 8)Які мірки необхідно знати для пошиву спідниці? (Обхват талії, стегон і довжина спідниці)Що означає економічно розкроїти тканину? (Використати площу тканини максимально)Які шляхи вирішення поставленої проблеми? (Оптимальний варіант: з'ясувати, при якій ширині низу клина в розкрої залишки тканини будуть мати максимальну площу)Вказівки до роботи: Ескіз і розрахунки виконувати для половини кількості клинів, тому що друга половина повторює першу. Ескіз і малюнки виконувати в довільному форматі. Завдання. Економічно розкроїти деталі спідниці в клини шириною тканини 90 см за умови, що довжина спідниці повинна бути не менше трикратної ширини низу клина спідниці.І варіант - спідниця у 6 клинів, розмір 88/96, напівобхват талії - 33 см.ІІ варіант - спідниця у 8 клинів, розмір 92/100, напівобхват талії - 36 см.

Постановка перед учнями проблемних ситуацій та вибір оптимальних шляхів до їх вирішування. У швацькому виробництві застосовуються обкантувальні стрічки, скісні бейки, найрізноманітніші види тасьми, а також рулони тканин, флизеліну, синтепону, ватину. Всі вони мають якісну характеристику на довжину, ширину та інше. Після того як ці матеріали побували у роботі, може виникнути необхідність знати залишок метражу в котушці чи рулоні. Замір вручну шляхом перемотки неможливий. Проблема: як бути? (Шляхи вирішування: тут ми маємо справу з циліндром. Зробити заміри зовнішнього та внутрішнього радіусів, висоти та обчислити різницю об'ємів. Знаючи об'єм, товщину, зможемо знайти площу, а знаючи ширину, знайдемо довжину, тобто метраж)Задача. Скільки метрів обкантувальної стрічки в котушці, якщо висота і радіус відповідно 2 см, 5 см, 12 см?При виготовленні м'яких іграшок, чохлів, валиків, подушок, пошиві сумок, циркових і новорічних костюмів виникають задачі на обчислення розмірів викрійок, що мають форму циліндра, конуса, часток кулі, а також треба вирішувати задачу про найменшу площу необхідної тканини на розкрій. Проблема: із обміру задано тільки об'єм деталі. Чи достатньо цього? Якщо ні, як бути? Як обчислити мінімальний крій?(Шляхи вирішування: одного об'єму недостатньо. Встановити самостійно ще якийсь замір (радіус чи висоту) нераціонально, тому що важливо мати загальне рішення. Значить треба обрати якусь залежність між радіусом та висотою. Щоб знайти мінімум площі тканини, допоможе похідна)