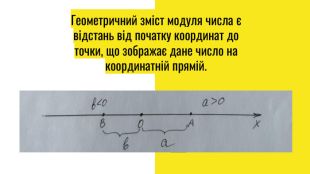
Презентація: Модуль дійсного числа
Про матеріал
Узагальнення знань учнів про модуль дійсного числа.Формувати вміння знаходити модуль дійсного числа. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






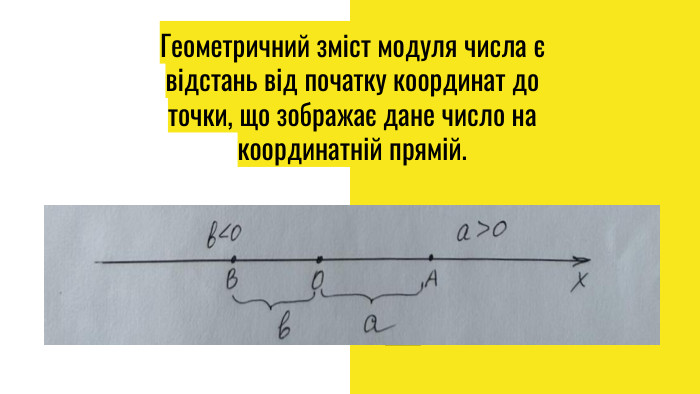


![Розглянемо приклади:1. Розв'язати рівняння |x| = 5x ]=5 означає геометрично, що відстань х до початку координатдорівнює 5, x = 5 або x = - 5 Відповідь: x = +/- 52. Розв'язати рівняння |x + 3| = 2 . Запишемо |x - (- 3)| = 2 , це геометрично означає, що відстань від точки -3 до точки x = 2 Відклавши від точки -3 на координатній прямій відрізок довжиною 2 (праворуч і ліворуч) одержимо x = - 1 або x = - 5 . Відповідь: -1; -5. Розглянемо приклади:1. Розв'язати рівняння |x| = 5x ]=5 означає геометрично, що відстань х до початку координатдорівнює 5, x = 5 або x = - 5 Відповідь: x = +/- 52. Розв'язати рівняння |x + 3| = 2 . Запишемо |x - (- 3)| = 2 , це геометрично означає, що відстань від точки -3 до точки x = 2 Відклавши від точки -3 на координатній прямій відрізок довжиною 2 (праворуч і ліворуч) одержимо x = - 1 або x = - 5 . Відповідь: -1; -5.](/uploads/files/1043864/441173/502282_images/9.jpg)