Урок-презентація "Алгебра. Застосування похідної,10"
Про матеріал
Розробка уроку у вигляді презентації з алгебри на тему " Застосування похідної" для учнів 10 класу Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





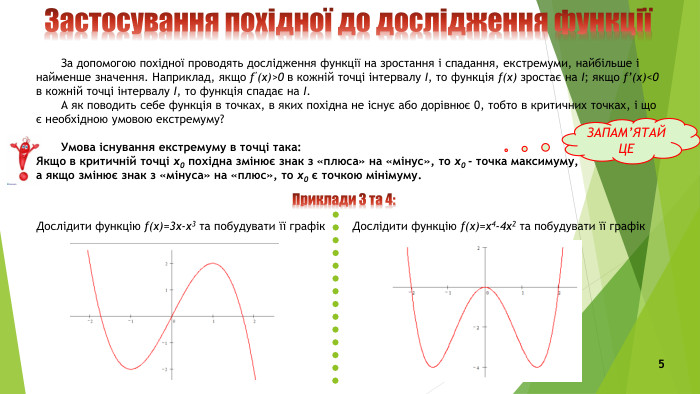
![Найменше і найбільше значення функції. Задача Дідони Фінікійська царівна Дідона, рятуючись від переслідувань свого брата, відправилася на захід вздовж берегів Середземного моря, де шукала собі пристановища. На узбережжі Туніської затоки вона почала вести переговори з Ярбом про купівлю для себе землі. І попросила в нього зовсім мало – стільки, скільки можна «обгородити шкірою з бика». І коли Дідона і Ярб дійшли згоди, Дідона порізала шкіру бика на тоненькі смужки, зв’язала їх і обгородила ними велику територію, чого Ярб не чекав. На ній Дідона побудувала фортецю, а поблизу неї – місто Карфаген. Поміркуємо, яку найбільшу кількість землі можна обгородити шкірою з бика? Або, мовою математики, яка із замкнених кривих, що має задану довжину, може охопити найбільшу площу? Принцип розв’язування задачіФактично, нам треба знайти найбільше значення деякої неперервної функції на відрізку [a; b]. А для цього слід: 1) знайти критичні точки функції;2) обчислити значення функції в критичних точках, що належать відрізку, та на кінцях відрізку;3) вибрати серед усіх обчислених значень функції найбільше. Цю класичну задачу сама Дідона розв’язала правильно. А кривою, що охоплює найбільшу площу, є круг – найдосконаліша, на думку Піфагора, плоска фігура.5 Приклад 5: Серед прямокутників, вписаних у коло, знайти прямокутник найбільшої площі. Найменше і найбільше значення функції. Задача Дідони Фінікійська царівна Дідона, рятуючись від переслідувань свого брата, відправилася на захід вздовж берегів Середземного моря, де шукала собі пристановища. На узбережжі Туніської затоки вона почала вести переговори з Ярбом про купівлю для себе землі. І попросила в нього зовсім мало – стільки, скільки можна «обгородити шкірою з бика». І коли Дідона і Ярб дійшли згоди, Дідона порізала шкіру бика на тоненькі смужки, зв’язала їх і обгородила ними велику територію, чого Ярб не чекав. На ній Дідона побудувала фортецю, а поблизу неї – місто Карфаген. Поміркуємо, яку найбільшу кількість землі можна обгородити шкірою з бика? Або, мовою математики, яка із замкнених кривих, що має задану довжину, може охопити найбільшу площу? Принцип розв’язування задачіФактично, нам треба знайти найбільше значення деякої неперервної функції на відрізку [a; b]. А для цього слід: 1) знайти критичні точки функції;2) обчислити значення функції в критичних точках, що належать відрізку, та на кінцях відрізку;3) вибрати серед усіх обчислених значень функції найбільше. Цю класичну задачу сама Дідона розв’язала правильно. А кривою, що охоплює найбільшу площу, є круг – найдосконаліша, на думку Піфагора, плоска фігура.5 Приклад 5: Серед прямокутників, вписаних у коло, знайти прямокутник найбільшої площі.](/uploads/files/5540379/438668/493999_images/6.jpg)