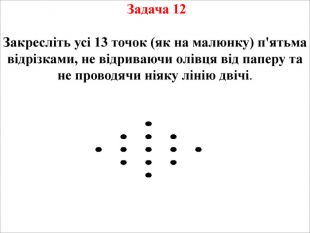
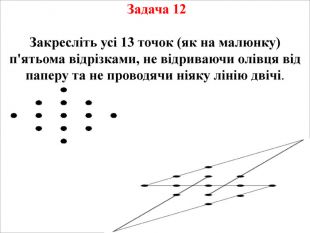
Презентація на тему "Логічні задачі"

ЛогічніЗадачі

Про математику і логіку. Той факт, що вся математика – це символічна логіка, є одним з найбільших відкриттів нашого часу, і як тільки цей факт установлено, дальше дослідження принципів математики полягає в аналізі самої символічної логіки. Б. Рассел. Математика і логіка розвивались останнім часом паралельно; логіка стала математичнішою, а математика – логічнішою. Внаслідок цього тепер стало зовсім неможливо провести лінію поділу між ними; фактично вони стали одним цілим. Вони відрізняються як дитина і доросла людина: логіка – це юність математики, а математика – зрілий вік логіки …Б. Рассел

Задача 1 У закритій кімнаті є 3 лампочки розжарювання. Кожна лампочка має свій вимикач. Вимикачі є в другій кімнаті. Як при допомозі користування вимикачами при одному заході в кімнату можна встановити, який вимикач відповідає якій лампочці?

Задача 1 У закритій кімнаті є 3 лампочки розжарювання. Кожна лампочка має свій вимикач. Вимикачі є в другій кімнаті. Як при допомозі користування вимикачами при одному заході в кімнату можна встановити, який вимикач відповідає якій лампочці?Розв’язок: Лампочки: 1; 2; 3 Вимикачі: А; Б; В Включити один із вимикачів А або Б або В і через певний час виключити. - Включити інший вимикач і залишити включену лампочку- Зайти у кімнату з лампочками і визначити: лампочка, що горить відповідає другому вимикачеві; лампочка, яка є теплою відповідає першому вимикачеві; холодна лампочка відповідає третьому вимикачеві.

Задача 2 У приватну гостинницю приїхав мандрівник. Грошей для розрахунку він не мав, але мав золотий ланцюжок, у якому було 6 кілець, з’єднаних послідовно. Господар погодився на розрахунок кільцями. Одна доба - одне кільце. Розрахунок кожного дня. Крім цього господар погодився розрізати лише одне кільце. Як вдалося мандрівнику прожити 6 днів?

Задача 2 У приватну гостинницю приїхав мандрівник. Грошей для розрахунку він не мав, але мав золотий ланцюжок, у якому було 6 кілець, з’єднаних послідовно. Господар погодився на розрахунок кільцями. Одна доба - одне кільце. Розрахунок кожного дня. Крім цього господар погодився розрізати лише одне кільце. Як вдалося мандрівнику прожити 6 днів?Розв’язок. Першого дня мандрівник розраховується одним розрізаним кільцем; другого – подвійним кільцем і повертає собі розрізане кільце; третього – потрійним кільцем і повертає собі подвійне; четвертого – розрізаним кільцем; п’ятого – подвійним кільцем і повертає собі розрізане кільне; шостого – розрізаним кільцем

Задача 3 Діаметр глибокого озера 200 м. На березі росте дуб. В центрі озера на невеличкому острові також росте дуб. Туристу, який має шнур довжиною у 200 м. потрібно перебратись з берега на цей острів. Плавати турист не вміє і нічого іншого не має. Як туристу перебратися?Кріплення у загальну довжину не враховується.

Задача 3 Діаметр глибокого озера 200 м. На березі росте дуб. В центрі озера на невеличкому острові також росте дуб. Туристу, який має шнур довжиною у 200 м. потрібно перебратись з берега на цей остів. Плавати турист не вміє і нічого іншого не має. Як туристу перебратися?Розв’язок. Закріпити шнур до дуба, який росте на березі. Обійти озеро по берегу. Закріпити другий кінець шнура до цього ж дуба на березі. Середина шнура закріпиться самостійно до дуба у центрі озера. Перебратись до центра озера по шнуру.

Задача 4 Один біолог відкрив дивовижний різновид амеб. Кожна з них через хвилину ділиться на дві. У пробірку біолог кладе одну амебу, і через годину вся пробірка виявляється заповненою амебами. Скільки треба було б часу, щоб уся пробірка заповнилася амебами, якби в неї спочатку поклали не одну амебу, а дві?

Задача 4 Один біолог відкрив дивовижний різновид амеб. Кожна з них через хвилину ділиться на дві. У пробірку біолог кладе одну амебу, і через годину вся пробірка виявляється заповненою амебами. Скільки треба було б часу, щоб уся пробірка заповнилася амебами, якби в неї спочатку поклали не одну амебу, а дві?Розв’язок. Оскільки кожної хвилини амеби діляться на дві і заповнення пробірки здійснюється через 60 хв., то якщо початок поділу здійснюється з двома амебами, тобто з другої хвилини. Отже, заповнення колби здійсниться через 59 хв.

Задача 5 Дано 2 бікфордових шнури різної довжини і різної швидкості горіння. Кожен шнур згоряє рівно за 1 год, проте його горіння не рівномірне (наприклад: 3/4 шнура може горіти 5 хв, а решту - 55 хв.) Як за допомогою горіння шнурів можна встановити 45 хв. горіння?

Задача 5 Дано 2 бікфордових шнури різної довжини і різної швидкості горіння. Кожен шнур згоряє рівно за 1 год, проте його горіння не рівномірне (наприклад: 3/4 шнура може горіти 5 хв, а решту - 55 хв.) Як за допомогою горіння шнурів можна встановити 45 хв. горіння?Розв’язок. Підпалюємо обидва шнури, причому один з них із двох сторін. Як тільки згорить той, що підпалено із двох сторін, пройшло 30 хв. Підпалюємо інший з другої сторони. Оскільки він уже горів 30 хв, то буде горіти тільки 30/2=15 хв. Маємо 45 хв, починаючи з моменту підпала.

Задача 6 Чоловік знаходиться на острові, який розміщений посередині річки Ніл. В річці багато крокодилів. Острів загорівся. Полум’я велике, не перестрибнути. Утікати нікуди. Як спастись туристу (не загинути)?

Задача 6 Чоловік знаходиться на острові, який розміщений посередині річки Ніл. В річці багато крокодилів. Острів загорівся. Полум’я велике, не перестрибнути. Утікати нікуди. Як спастись туристу (не загинути)?Розв’язок Вирвати шмут високої трави. Запалити його і запалити острівок біля річки в напрямку поширення полум’я. Коли вигорить цей острівок, пререйти на цей згорений острівок. Поширення великого вогню не перейде на невеличкий острівок. Спасіння.

Задача 7 Як відміряти 15 хвилин, маючи семи- й одинадцяти хвилинні пісочні годинники?

Задача 7 Як відміряти 15 хвилин, маючи семи- й одинадцяти хвилинні пісочні годинники?Розв’язок. Запускаю 7-хвилинний і 11-хвилинний годинники. Після 7 хвилин перевертаю його. Разом з 11-хвилинним годинником 7-хвилинний сипле пісок 4 хвилини. Після завершення пересипання 11-хвилинного годинника знову повертаю 7-хвилинний, у якому є 4 хвилини піску. 11+4=15

Задача 8 Як із 100 м висоти, маючи шнур, довжиною 75 м і ніж спуститись вниз? Посередині висоти є перекладина, до якої можна закріпитьи шнур. Шнур можна розрізати. Закріплення шнура у загальну довжину не входить.

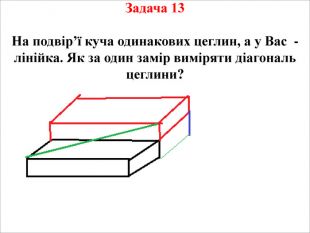
Задача 8 Як із 100 м висоти, маючи шнур, довжиною 75 м і ніж спуститись вниз? Посередині висоти є перекладина, до якої можна закріпитьи шнур. Шнур можна розрізати. Закріплення шнура у загальну довжину не входить. Розв’язок. Шнур розрізати на довжини 25 м. і 50м. Шнур довжиною 25 м. закріпити до балки А і зробити петлю в другому кінці шнура. Опуститись на 25 м. Шнур довжиною 50 м. зігнути наполовину і опуститись на ньому наступні 25 м. Зняти шнур у 50м., прикрапити його до балки С та опуститись на наступні 50 м.

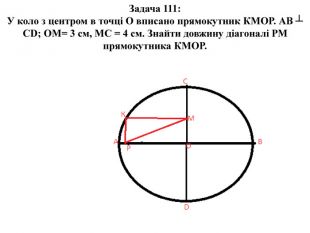
 Задача 110. В одному буддійському храмі на висоті 100 метрів до стелі прироблені два золоті канати, довжиною по 100 метрів кожний. Обидва канати звисають до підлоги. Вони висять на близькій відстані, наприклад, - півметра. У храм заходить Злодій - спритний акробат, що вміє лазити по канатах і відрізати їх. Якщо Злодій звалиться на землю з висоти менше 10 метрів, то він задоволений. Якщо з більшої висоти – вмирає (лікування йому вже не допоможе). Як йому вдалося забрати з храму не менше 190 метрів золотого канату, а не лише 110? (канати вважати легкими).

 Задача 110. В одному буддійському храмі на висоті 100 метрів до стелі прироблені два золоті канати, довжиною по 100 метрів кожний. Обидва канати звисають до підлоги. Вони висять на близькій відстані, наприклад, - півметра. У храм заходить Злодій - спритний акробат, що вміє лазити по канатах і відрізати їх. Якщо Злодій звалиться на землю з висоти менше 10 метрів, то він задоволений. Якщо з більшої висоти – вмирає (лікування йому вже не допоможе). Як йому вдалося забрати з храму не менше 190 метрів золотого канату, а не лише 110? (канати вважати легкими).  Розв’язок: Залазить по одному з канатів на висоту 95 метрів і відрізає від іншого 95 метрів. Частину в 5 метрів, що залишилася висіти, прив'язує до першого канату в точці поділу на 5 й 95 метрів. Виходить, петля створена зв'язаними 5 метрами першого канату й 5 метрами другого канату. Після чого Злодій спускається в низ і зв'язує 95 метрів другого канату, що впав, з ще висячим першим. Після чого, вільний кінець отриманого 195 метрового канату пропускає через петлю. Угорі він ріже перший канат у точці 5 й 95 метрів. Виходить, що через петлю 10 метрів звисає канат довжиною 190 метрів. Злодій спускається униз і забирає 190 метрів.

Задача 111  Як, маючи в наявності тільки креслярський косинець і олівець, точно визначити центр кола (у цьому випадку колеса)?

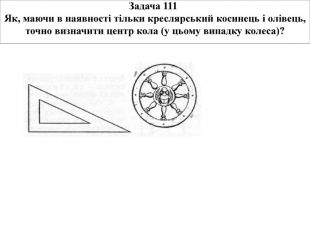
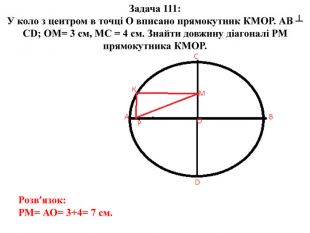
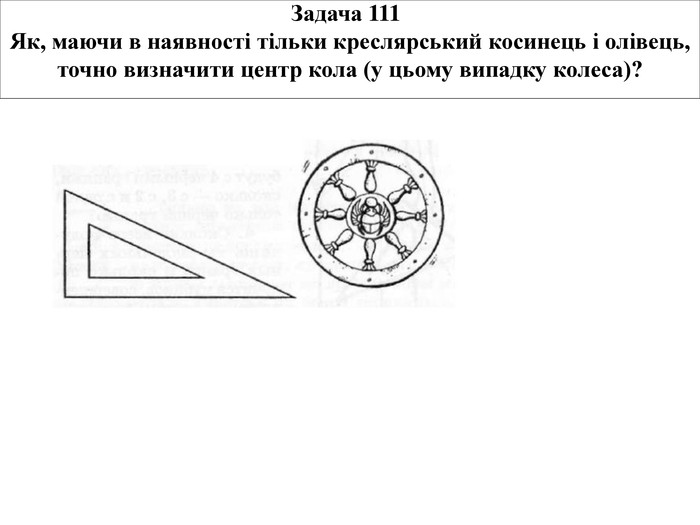
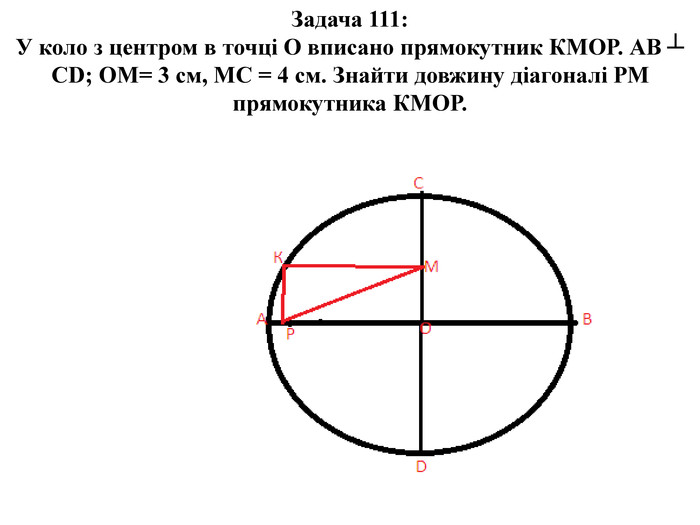
Розв’зок задачі 111 Вписаний кут - це такий, вершина якого лежить на окружності. А по величині він дорівнює половині тієї дуги, на яку опираються його кінці. І якщо вписаний кут опирається на діаметр, то дуга між його кінцями - рівно половина окружності, або 180 градусів, а сам кут - половина цієї дуги, тобто 90 градусів, або прямий.  Потрібно покласти креслярський косинець на колесо - так, щоб вершина його прямого кута виявилася на ободі. Тепер потрібно помітити, де перетинають обід обидва катети косинця. Через ці дві точки провести пряму й одержати перший діаметр (він прокреслений пунктиром). Потім точно так само провести й інший діаметр. А де перетинаються всі діаметри? Звичайно ж, у центрі!

Задача 105 Три хлопчика ділять 24 яблука. Поки у них є три купки: 11, 7 і 6 яблук відповідно, але вони хочуть поділити їх порівну. Один з них запропонував двом іншим таке парі: - Ви повинні будете зрівняти кількість яблук в купках, але строго по моїй системі: з однієї купи берете стільки яблук, скільки їх у тій купці, куди ви додавати збираєтеся. Але зробити це ви повинні строго за 3 перекладання. Вкладетеся - всі яблука ваші, немає - вони мої. - Давай! - погодилися двоє. Подумали з хвилинку і виграли суперечку. Питання: як вони це зробили? 

Задача 105 Три хлопчика ділять 24 яблука. Поки у них є три купки: 11, 7 і 6 яблук відповідно, але вони хочуть поділити їх порівну. Один з них запропонував двом іншим таке парі: - Ви повинні будете зрівняти кількість яблук в купках, але строго по моїй системі: з однієї купи берете стільки яблук, скільки їх у тій купці, куди ви додавати збираєтеся. Але зробити це ви повинні строго за 3 перекладання. Вкладетеся - всі яблука ваші, немає - вони мої. - Давай! - погодилися двоє. Подумали з хвилинку і виграли суперечку. Питання: як вони це зробили? Розв’язок: Початок: 11-7-6/ 1-й хід: 11-1-12 // 2-ий хід: 10-2-12/// 3-ій хід: 8-4-12//// Підсумок: 8 8 8або. Початок: 11-7-6//1-й хід: 4-14-6///2-ий хід: 4-8-12//// Підсумок: 8 8 8/

Задача 104. На стоянці місця для автомобілів пронумеровано. Під яким номером стоїть автомобіль?

Задача 104. На стоянці місця для автомобілів пронумеровано. Під яким номером стоїть автомобіль?Розв’язок:87; дзеркальне відбиття

Задача 107. Фермерка принесла на базар качани капусти і продала трьом покупницям. Перша взяла половину всіх качанів і ще півкапустини. Друга купила половину качанів, що залишились і ще півкапустини. Третя покупниця взяла останній качан. Скільки качанів капусти винесла на базар колгоспниця?

Задача 107. Фермерка принесла на базар качани капусти і продала трьом покупницям. Перша взяла половину всіх качанів і ще півкапустини. Друга купила половину качанів, що залишились і ще півкапустини. Третя покупниця взяла останній качан. Скільки качанів капусти винесла на базар колгоспниця?Розв’язок: Розв’язуватимемо задачу з кінця. Третя покупниця взяла останній качан. Якби вона взяла ще півкачана замість другої покупниці, то це було б половина решти. Отже решта: (1+0.5)*2=3. Якби перший покупець не брав ще півкачана, то залишилася б половина від всіх качанів. Отже, всіх качанів було: (3+0.5)*2=7. Відповідь: 7 качанів

Задача 113: Дано кут 54 градули. При допомозі циркуля і лінійки поділити цей кут на 3 частини.

Задача 113: Дано кут 54 градули. При допомозі циркуля і лінійки поділити цей кут на 3 частини. Розв’язок: 54*2= 108; 108-90= 18. Будую кут двічі кут 54 градуси. Отримаємо кут 108 градусів. Віднімаю від нього кут 90 градусів. Утворився кут 18 градусів. Проводжу бісектрису кута 54-18= 36 градусів.

Задача 9 Рівність зображена на малюнку невірна, перекладіть один сірник так, щоб вона виконувалося з точністю до 0.001.

Задача 9 Рівність зображена на малюнку невірна, перекладіть один сірник так, щоб вона виконувалося з точністю до 0.001. Розв’язок22/7=Пі (3,14)

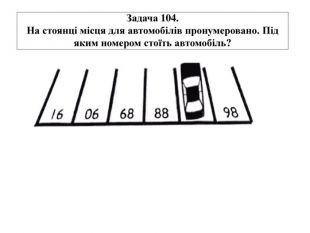
Задача 10 Через міст треба перейти чотирьом туристам. Через 17 хвилин міст впаде у пропасть. Туристи можуть перейти (якщо йдуть по одному) через: перший - 1 хв, другий - 2 хв, третій - 5 хв, четвертий - 10хв. Через міст може пройти лише два туристи. Ніч. Повна темнота. Ліхтар один. Міст драбинний. Щаблі розміщені не однаково. Без ліхтаря пройти по мосту не можна. Як перейти усім через міст за 17 хвилин.

Задача 10 Через міст треба перейти чотирьом туристам. Через 17 хвилин міст впаде у пропасть. Туристи можуть перейти (якщо йдуть по одному) через: перший - 1 хв, другий - 2 хв, третій - 5 хв, четвертий - 10хв. Через міст може пройти лише два туристи. Ніч. Повна темнота. Ліхтар один. Міст драбинний. Щаблі розміщені не однаково. Без ліхтаря пройти по мосту не можна. Як перейти усім через міст за 17 хвилин. Розв’язок

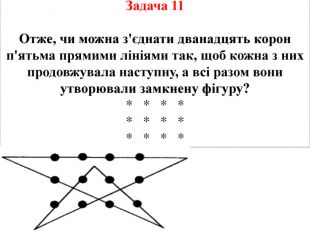
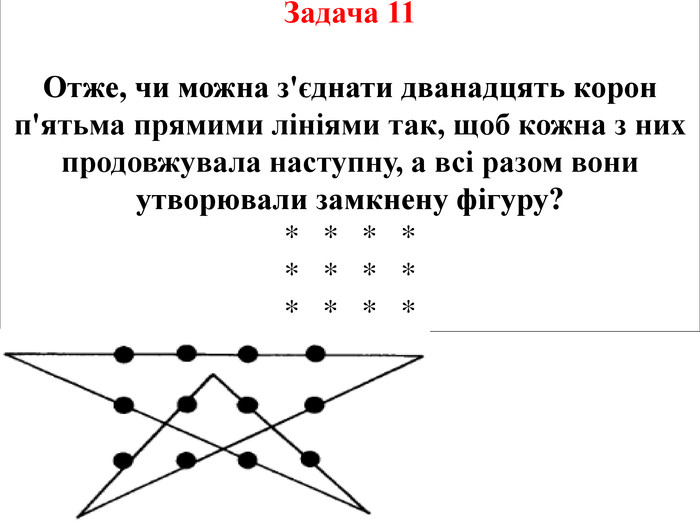
Задача 11 Фермер мав репутацію досить ексцентричного джентльмена. Складаючи план будівлі нових загонів для своїх дев'яти телиць-рекордсменок, він велів своїм працівникам побудувати чотири загони, причому в кожному з них повинна розташовуватися непарна кількість тварин. Цікаво, чи вдалося працівникам виконати умову причепливого хазяїна?

Задача 11 Фермер мав репутацію досить ексцентричного джентльмена. Складаючи план будівлі нових загонів для своїх дев'яти телиць-рекордсменок, він велів своїм працівникам побудувати чотири загони, причому в кожному з них повинна розташовуватися непарна кількість тварин. Цікаво, чи вдалося працівникам виконати умову причепливого хазяїна?Розв’язок

Задача 13 На подвір’ї куча одинакових цеглин, а у Вас - лінійка. Як за один замір виміряти діагональ цеглини?

Задача 13 На подвір’ї куча одинакових цеглин, а у Вас - лінійка. Як за один замір виміряти діагональ цеглини?

Задача 14 На плиті можна розмістити 2 коржі. Печеться один корж з одного боку 1 хв. Як спекти 3 коржі за 3 хвилини з двох боків?

Задача 14 На плиті можна розмістити 2 коржі. Печеться один корж з одного боку 1 хв. Як спекти 3 коржі за 3 хвилини з двох боків?Розв’язок11/ 12, 21/ 22, 31/ 3211 і 21 - 1 хв12 і 31 – 1 хв22 і 32 – 1 хв

Задача 15 О третій год дня годинник б’є за 6 с. Скільки часу годинник буде бити опівночі?

Задача 15 О третій год дня годинник б’є за 6 с. Скільки часу годинник буде бити опівночі?Розв’язок. Між кожними ударами годинника є 3 сек., а не 2 сек. Опівночі буде таких проміжків буде 11, а не 12, оскільки перший урар не має проміжку. 11*3=33 (сек).

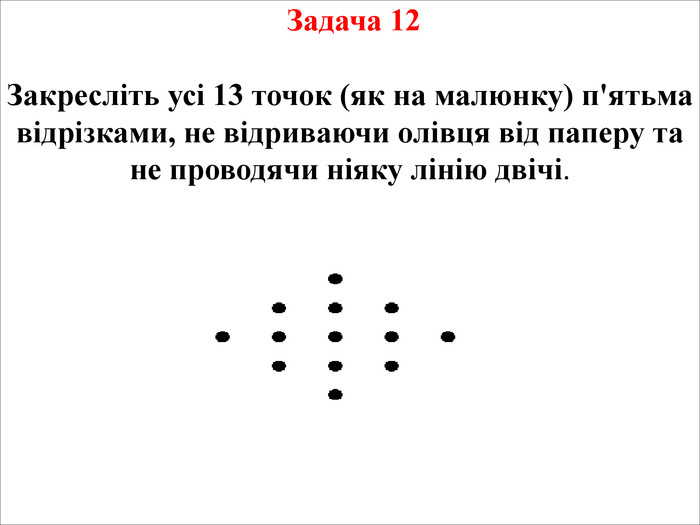
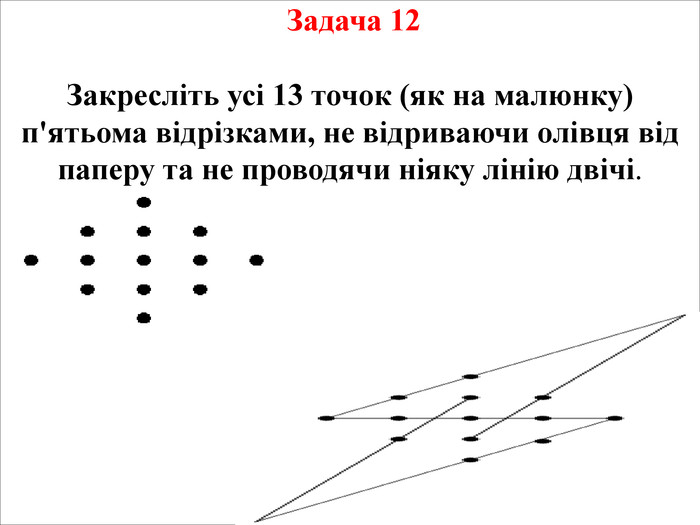
Задача 16 Ви захворіли, пішли до лікаря котрий дав вам по три пігулки у баночках А та В. Пігулки ідентичні зовні, але мають різний ефект. Ви повинні кожен день випивати разом пігулку із баночки А та пігулку із баночки В, так протягом трьох днів. Рецепт не можна порушувати. Але вранці після першого дня ви побачили, що на столі лежать три пігулки, баночка В порожня, а в баночці А лише одна пігулка. Як вам діяти, щоб закінчити лікування не порушуючи рецепту?

Задача 16 Ви захворіли, пішли до лікаря котрий дав вам по три пігулки у баночках А та В. Пігулки ідентичні зовні, але мають різний ефект. Ви повинні кожен день випивати разом пігулку із баночки А та пігулку із баночки В, так протягом трьох днів. Рецепт не можна порушувати. Але вранці після першого дня ви побачили, що на столі лежать три пігулки, баночка В порожня, а в баночці А лише одна пігулка. Як вам діяти, щоб закінчити лікування не порушуючи рецепту?Розв’язок. Решту таблеток ділимо пополам і робимо 2 купки. Другого дня вживаємо половинки таблеток з одної купки, третього – другої.

Задача 111: У коло з центром в точці О вписано прямокутник КМОР. АВ ┴ СD; ОМ= 3 см, МС = 4 см. Знайти довжину діагоналі РМ прямокутника КМОР.

Задача 111: У коло з центром в точці О вписано прямокутник КМОР. АВ ┴ СD; ОМ= 3 см, МС = 4 см. Знайти довжину діагоналі РМ прямокутника КМОР. Розв’язок: РМ= АО= 3+4= 7 см.

Задача 125Із 12 сірників скласти 5 квадратів. Квадрат у квадраті не рахується два квадрати. Сірники не накладати, не ламати, не різати.

Задача 125Із 12 сірників скласти 5 квадратів. Квадрат у квадраті не рахується два квадрати. Сірники не накладати, не ламати, не різати. Розв’язок:8 сірників – зовнішні сірники (не нарисовано). Чотири сірники внутрішні розміщено головками в різні сторони. Середина – утворений маленький квадрат (4+1)

Задача 17

Задача 17

Задача 11 Отже, чи можна з'єднати дванадцять корон п'ятьма прямими лініями так, щоб кожна з них продовжувала наступну, а всі разом вони утворювали замкнену фігуру? * * * ** * * ** * * *

Задача 11 Отже, чи можна з'єднати дванадцять корон п'ятьма прямими лініями так, щоб кожна з них продовжувала наступну, а всі разом вони утворювали замкнену фігуру? * * * ** * * ** * * *

 Задача 12 Закресліть усі 13 точок (як на малюнку) п'ятьма відрізками, не відриваючи олівця від паперу та не проводячи ніяку лінію двічі.

 Задача 12 Закресліть усі 13 точок (як на малюнку) п'ятьома відрізками, не відриваючи олівця від паперу та не проводячи ніяку лінію двічі.

Задача 18 У морі стоїть корабель. З палуби корабля опущений трап до води. Відстань між щаблями трапу - 20 см. Зверху трапу до води - 12 щаблів. Під час припливу вода піднялося на 60 см. Скільки щаблів буде видно над водою?

Задача 18 У морі стоїть корабель. З палуби корабля опущений трап до води. Відстань між щаблями трапу - 20 см. Зверху трапу до води - 12 щаблів. Під час припливу вода піднялося на 60 см. Скільки щаблів буде видно над водою?Розв’язок 18 Корабель піднімається разом з припливом

Задача 19 Чотирикутне поле оточене ровом, ширина якого всюди однакова. Дано дві дошки, довжина кожної з яких дорівнює ширині рову, але трошки менша. Потрібно за допомогою цих дощок улаштувати перехід через рів.

Задача 19 Чотирикутне поле оточене ровом, ширина якого всюди однакова. Дано дві дошки, довжина кожної з яких дорівнює ширині рову, але трошки менша, і потрібно за допомогою цих дощок улаштувати перехід через рів. Розв’язок

Задача 20 Скільки в мене квітів, якщо всі з них окрім двох - троянди, всі окрім двох - тюльпани, і всі окрім двох – маргаритки?

Задача 20 Скільки в мене квітів, якщо всі з них окрім двох - троянди, всі окрім двох - тюльпани, і всі окрім двох – маргаритки?Розв’язок: Три

Задача 21 Охоронець і засуджений вирішили зіграти гру на круглій дошці з викладанням почергово круглих шашок. Виграє той, хто перший не матиме місця покласти шашку. Шашки не повинні накладатися. Як виграти охоронцеві?

Задача 21 Охоронець і засуджений вирішили зіграти гру на круглій дошці з викладанням почергово круглих шашок. Виграє той, хто перший не матиме місця покласти шашку. Шашки не повинні накладатися. Як виграти охоронцеві? Розв’язок: Першим на дошку ставить шашки засуджений. Охоронець ставить шашки симетрично відносно центру.

Задача 22 У психлікарні пацієнт питає лікаря, як він визначає потребу перебування пацієнта у лікарні. Лікар відповів, що дає пацієнту ложку, стакан і ведро щоб вилити воду з ванни. Пацієнт відповів, що взяв би ложку і ведро. Швидше буде. Тоді лікар визначив стан пацієнта. Який стан пацієнта?

Задача 22 У психлікарні пацієнт питає лікаря, як він визначає потребу перебування пацієнта у лікарні. Лікар відповів, що дає пацієнту ложку, стакан і ведро щоб вилити воду з ванни. Пацієнт відповів, що взяв би ложку і ведро. Швидше буде. Тоді лікар визначив стан пацієнта. Який стан пацієнта?Розв’язок: Стан пацієнта: Пацієнт хворий, оскільки він не використав корка у ванні.

Задача 23 Для того, щоб перейти туристу до бабусі через довгий міст необхідно пройти 7 постів. На кожному пості туристу потрібно віддати половину булочок, що є у нього і йому повертається одна булочка. І так на кожному пості. Скільки треба придбати туристу булочок, щоб занести бабусі через міст дві булочки.

Задача 23 Для того, щоб перейти туристу до бабусі через довгий міст необхідно пройти 7 постів. На кожному пості туристу потрібно віддати половину булочок, що є у нього і йому повертається одна булочка. І так на кожному пості. Скільки треба придбати туристу булочок, щоб занести бабусі через міст дві булочки. Розв’язок: На першому пості турист віддає половину своїх булочок (1 булочку) і йому повертають одну булочку. В нього знову залишається дві булочки. Так само турист робить на кожному наступному пості. Відповідь: 2 булочки

Задача 24 Пальців у мене двадцять п’ять на одній руці і стільки ж на другій, а на ногах десять. Чи може таке бути?

Задача 24 Пальців у мене двадцять п’ять на одній руці і стільки ж на другій, а на ногах десять. Чи може таке бути?Розв’язок. Так, тому що на двох руках по 5 пальців і на ногах 10 бальців

Задача 25 На сході один старий, вмираючи, заповів трьом синам 19 верблюдів. Старшому сину – половину усіх верблюдів, середущому – четвертину, молодшому – п’яту частину. Брати сперечалися і не змогли поділити спадщину. Запросили мудреця, який приїхав до братів на верблюді і поділив їх спадщину. Як він це зробив?

Задача 25 На сході один старий, вмираючи, заповів трьом синам 19 верблюдів. Старшому сину – половину усіх верблюдів, середущому – четвертину, молодшому – п’яту частину. Брати сперечалися і не змогли поділити спадщину. Запросили мудреця, який приїхав до братів на верблюді і поділив їх спадщину. Як він це зробив?Розв’язок. Після смерті батька сини не могли виконати заповіт, тому вони запросили мудреця на допомогу. Мудрець приїхав на своєму верблюді і додав його до верблюдів синів (1+19=20). Старшому сину мудрець запропонував половину від 20, тобто 10 верблюдів. Середущому – четверту частину від 20, тобто 5 верблюдів, а молодшому – п’яту частину, тобто 4 верблюди. Одже: 10+5+4 = 19. Сів мудрець на свого двадцятого верблюда і поїхав додому.