Урок на тему: " Інтеграл в архітектурі"
ВІДКРИТИЙ УРОК
”ІНТЕГРАЛ В АРХІТЕКТУРІ”
11клас
ДЕВІЗ УРОКУ :” Три шляхи ведуть до знання: шлях роздумів- це шлях найблагородніший, шлях наслідування- це шлях найлегший і шлях досвіду - це шлях найгіркіший.” КОНФУЦІЙ.
Так будем же благородними !!!
ТЕМА уроку: Застосування інтегралу.
Мета уроку : узагальнити і систематизувати знання учнів з теми :”Застосування інтеграла для обчислення площ криволінійних фігур”.
Засоби навчання :
Таблиці ,підручники, робочі зошити.
Тип уроку :
Узагальнення і систематизація знань.
Очікувані результати :
- учні повторюють властивості інтеграла;
-повторюють способи розв’язання задач ;
-робитимуть логічні висновки, аналізуючи вивчений матеріал;
-поглиблять вміння оцінити свої знання.
Хід уроку:
- Організаційний момент.
Добрий день, шановні учні !
2 . Мотивація навчальної діяльності,тема та мета уроку.
Сьогодні у нас незвичайний урок,сьогодні ми познайомимся, як треба на практиці використовувати свої знання під час знаходження площ криволінійних фігур всесвітньо відомого творіння великого ГАУДІ “Храм святого сімейства”.
Тому три групи учнів отримали різні завдання.
1 група- узагальнити і систематизувати знання по темі: “ Інтеграл. Застосування інтеграла.”
2 група-підсумувати знання за формулою Ньютона- Лейбніца.
3група- інтеграл в архітектурі.
3 . Перевірка домашнього завдання.
На дошці записані розв’язки завдань. Учні самостійно перевіряють домашні завдання і на полях виставляють оцінки. В кінці уроку вчитель забирає зошити на перевірку.
- Актуалізація опорних знань.
-1.Інтегра́л — центральне поняття інтегрального числення, узагальнення поняття суми для функції, визначеній на континуумі. ... Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
Інтеграл широко застосовується в архітектурі так , як вичислює площу криволінійних ( нестандартних ) фігур .А як ми знаємо проектуючи будинки архітектори використовують різні криволінійні фігури для того , щоб прикрасити архітектуру і надати їй індивідуальний вигляд.
- Інтеграція простежується ще в давньому Єгипті, приблизно у 1800 до н.е., Московський математичний папірус демонструє знання формули об'єму січної піраміди. Першим відомим методом для розрахунку інтегралів є метод вичерпання Евдокса (приблизно 370 до н. е.), який намагався знайти площі і об'єми, розриваючи їх на нескінченну безліч частин, для яких площа або об'єм вже відомий. Цей метод був підхоплений і розвинутий Архімедом, і використовувався для розрахунку площ парабол і наближеного розрахунку площі круга. Аналогічні методи були розроблені незалежно в Китаї в 3-м столітті н.е Лю Хуейєм, який використовував їх для знаходження площі круга. Цей метод був згодом використаний Дзю Чонгши для знаходження об'єму сфери.
Таблиця висвічується на доскі
Хронологія розвитку поняття інтеграл
|
Дата |
Подія |
Автор |
Місце |
|
408 рік до н. е. |
Метод вичерпування для обчислення площ |
Евдокс |
Кнід |
|
287 рік до н. е. |
Механічний метод розрахунку об’ємів та площ |
Архімед |
Сіракузи |
|
1689 рік |
Внутрішній зв’язок між диференціюванням та інтегруванням |
Ньютон |
Вулсторп |
|
1702 рік |
Сформував основні поняття інтегрального числення, ввів сучасний символ інтегралу |
Лейбніц |
Лейпциг |
|
1830 рік |
Побудова визначеного інтегралу, введення невизначеного інтегралу як частинного випадку визначеного, деякі властивості визначеного інтегралу |
Коші |
Турин, Прага |
|
1857 рік |
Побудова інтегралу Рімана |
Ріман |
Німеччина |
|
1934 рік |
Дескриптивне визначення інтеграла |
Лебег |
Франція |
|
1894 рік |
Узагальнений визначений інтеграл |
Стілтьєс |
Тулуза |
|
1932 рік |
Отримання інтегралу, що дозволяє відновлювати елементарну функцію по її асимптотичній похідній |
Данжуа |
Франція |
|
1934 рік |
Хінчін |
Москва |
![\int \limits _{a}^{b}f(x)\,dx={\Bigl [}F(x){\Bigr ]}_{a}^{b}={\Bigl .}F(x){\Bigr |}_{a}^{b}](/uploads/files/835089/217413/233403_html/images/217413.001.png){kind=small}
Основне досягнення в області інтегрування відбулося в 17-му столітті із відкриттям фундаментальної теореми числення (відомої як формула Ньютона — Лейбніца) Ньютоном і Лейбніцем, незалежно один від одного. Теорема встановлює зв'язок між інтегруванням і диференціюванням. Зокрема, фундаментальна теорема числення дозволила вирішувати більш широкий клас задач. Ньютон і Лейбніц створили комплексну математичну теорію, що є не менш важливим. Ця теорія має назву - числення нескінченно малих величин, і дозволила здійснювати точний аналіз неперервних функцій. Ці основоположні роботи зрештою стали сучасним численням, в якому була використана нотація для інтегралів, що на пряму спирається на роботи Лейбніца.
Знак інтеграла (∫), був вперше використаний Лейбніцом наприкінці XVII століття. Цей символ утворився з букви ſ («довга s») — скорочення слова лат. ſumma (summa, сума).
Порівнюючи формули площі криволінійної трапеції
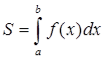і S = F(b) - F(a), робимо висновок:
якщо F(x) — первісна для функції f(x) на відрізку [а; b], то
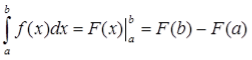
Ця формула правильна для будь-якої неперервної на відрізку [а; b] функції f(x), пов'язує поняття інтеграла й первісної для даної функції, є правилом обчислення інтегралів.
Для зручності запис різниці F(b) - F(a) прийнято скорочено позначати
.
При такому позначенні формула Ньютона-Лейбніца набирає вигляду
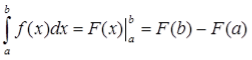
-3. Інтеграл в архітектурі .
Інтеграли в архітектурі використовуються в стилі «Модерн»
Загальна характеристика
Характерні риси стилю модерн в архітектурі: плавність, пластичність, декоративність. Основними його елементами є використання синусоїдальних ліній, стилізованих квітів, язиків полум'я, хвилястих ліній, запозичених у природи.
Прагнучи створити новий стиль, представники модерну відмовлялися від історичних запозичень стилю еклектики, використовували умисно примхливі, мінливі форми, вигадливі лінії, принципи асиметрії і вільного планування, нові технічні та конструктивні засоби для створення незвичайних, підкреслено індивідуалізованих будівель, де всі рішення підпорядковані єдиному образно-символічному задумові й орнаментальному ритмові.
Анто́ні Ґауді́-і-Курне́т - іспанський архітектор із Каталонії, новатор форми та один з найяскравіших представників стилів арт-нуво та модерн в архітектурному мистецтві. Більшість його робіт зосереджена в Барселоні.
Розглянемо застосування інтегралів в архітектурі на прикладі роботи Гауді – Храм Святого Сімейства .
Храм Святого Сімейства — кульмінація творчості Антоні Ґауді.
Цю величну церкву почали будувати ще у 1882 році на пожертви віруючих, хоча сам Ґауді був залучений до проекту лише 1884 р.
Трагічна загибель архітектора у 1926 р. не зупинила будівництво, воно продовжується й дотепер. Грандіозність задуму можна оцінити лише з того факту, що завершення його планується лише на 2026 рік.
Храм Святого Сімейства за задумом мав стати архітектурним втіленням Нового Заповіту, непорушності християнських вірувань.
Звідси й глибокий символізм храму. Згідно з проектом, храм має три фасади, кожний з яких має власну назву: західний — Різдва, східний — Страждань Христових, та південний — Вознесіння. Кожен фасад має чотири вежі висотою понад 100 метрів. Всього заплановано дванадцять башт, що символізують кількість апостолів.
З трьох фасадів за життя Ґауді майже збудований був лише один. Він має три входи, що символізують Віру, Надію та Милосердя, які прикрашені скульптурними групами за євангельськими сюжетами.
Окрім башт за проектом Храм увінчується ще чотирма — більш високими — вежами, що символізують чотири Євангелія. Головна дзвіниця Ісуса Христа, увінчана хрестом, матиме заввишки 170 метрів, а друга за висотою дзвіниця Діви Марії — 120 метрів.
Проектуючи храм ГАУДІ використовує «нефи»
На́ва, або неф —
поздовжня або поперечна частина простору монументальної споруди, що розташована між рядами колон, стовпів, арок або між зовнішньою стіною та поздовжньою колонадою або аркадою.
Арка́да —
ряд однакових формою та розміром арок, що спираються на колони або пілони. Найчастіше аркаду застосовують, коли влаштовують відкриті галереї, акведуки та багато інших споруд.
Коло́на —
«стовп» — архітектурно оброблена вертикальна опора, як правило, кругла в перерізі. Елемент тримальної конструкції споруд та архітектурних ордерів.
Піло́н —
• масивний стовп, який підтримує склепіння або пласкі перекриття; може бути елементом оформлення порталу будівлі, в'їзду в парк, місто тощо.
• пілонами вважаються опори прямокутного перетину в сучасних багатоповерхових конструкціях, що підтримують яруси, залиті монолітним залізобетоном. Пілон відрізняється від колони тим, що має круглий перетин.
Арфітектор використовує не стандартні форми, тому для обчислення площі використовують інтеграли.
Вирахуємо площі деяких арок Храму Святого Сімейства.
ЗАДАЧІ ПРАКТИЧНОГО ЗМІСТУ.
№1. Обчислити площу частини вітражу храму.
Знайти площу фігури, обмеженої параболою у= х2,віссю Ох і прямою х=к.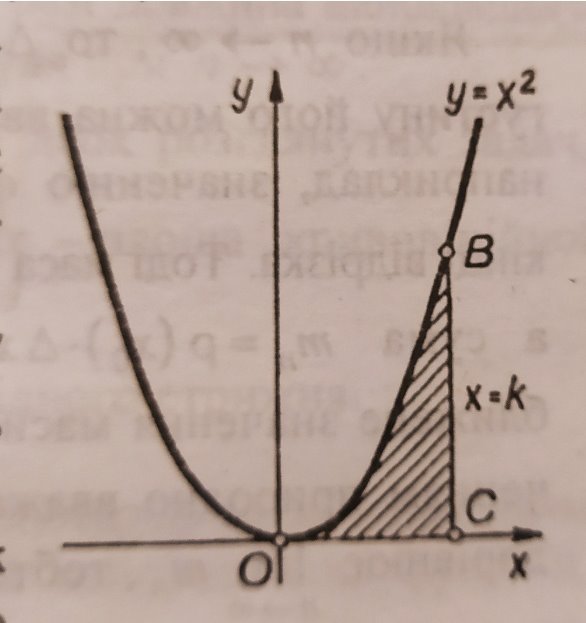 
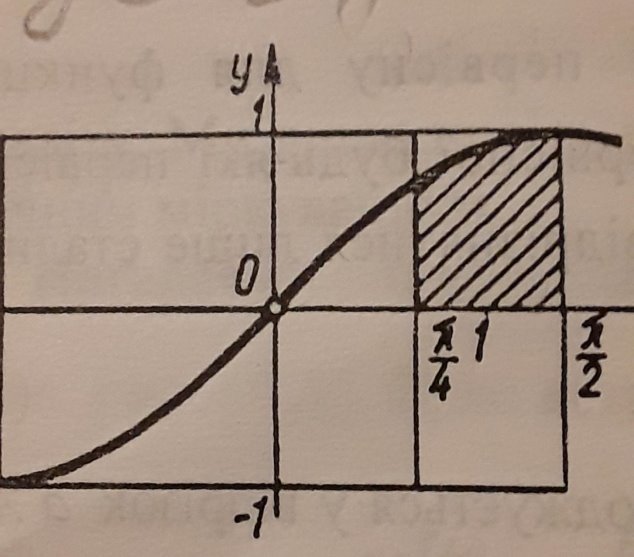
№2. Синусоїдою обмежена частина фасаду.
Обчислити за формулою Ньютона-Лейбніца площу фігури ,обмеженою зверху синусоїдою у =sinx, знизу-віссю
Ох, а з боків- прямими х=
/4 і х =/2.
№3. Пілястри обмежені кубічною параболою у= х3 ,віссю Ох та прямими х=2 і х=5.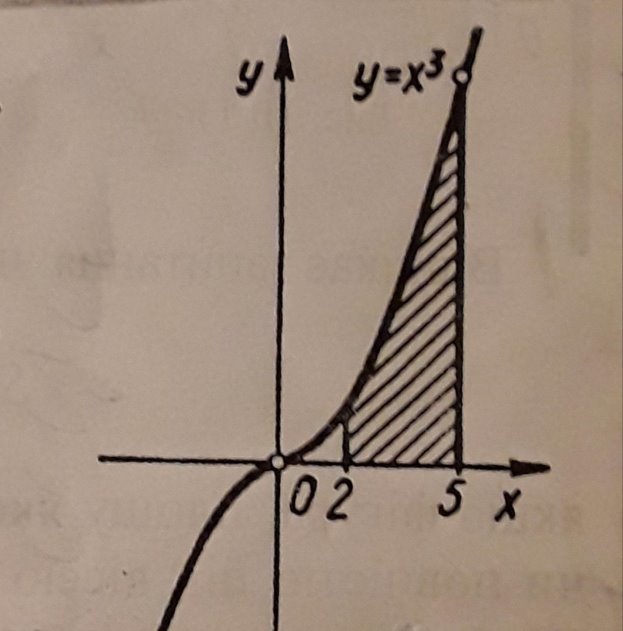 
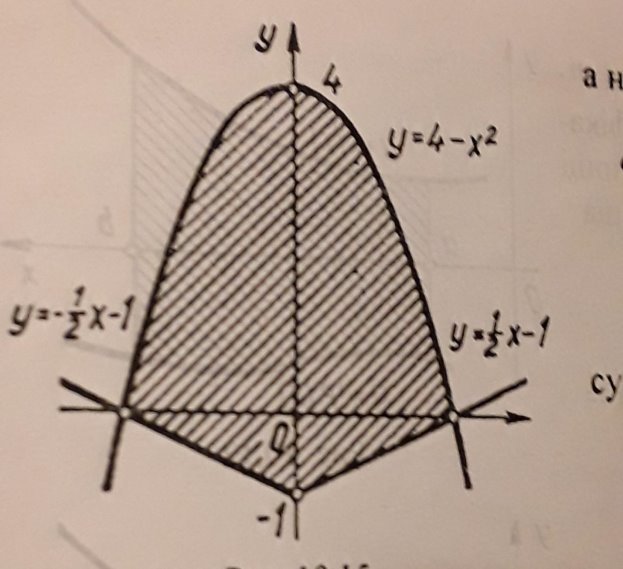
№4 Знайти площу вітражного вікна ,обмеженого параболою у=4-х 2 т та прямими у=-½х-1, у=1/2х-1
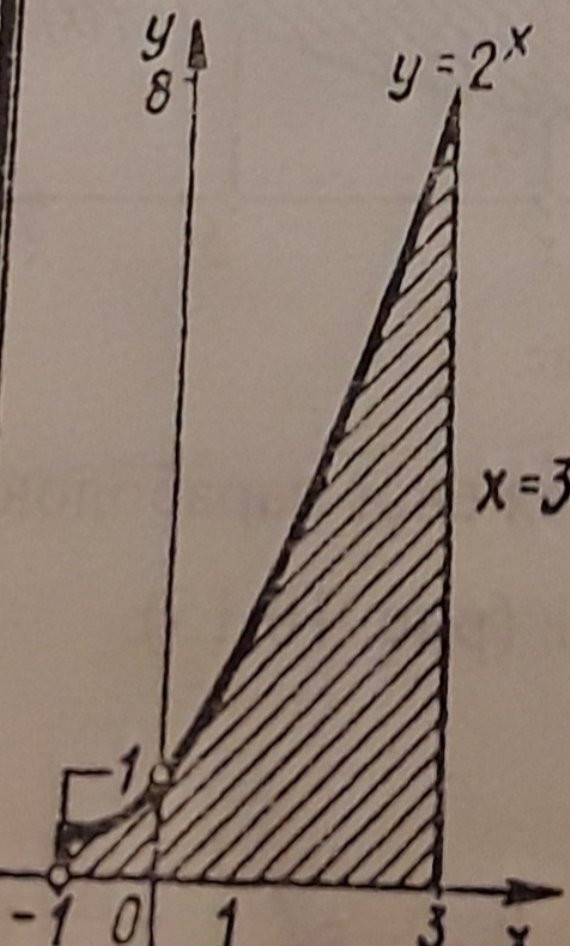
№5 Знайти площу колони ,обмежену лініями у=2х , у=0,
х=-1 ,х=3.
№6.Знайти площу нефу ,обмежену кривими у= х2, у=х3.
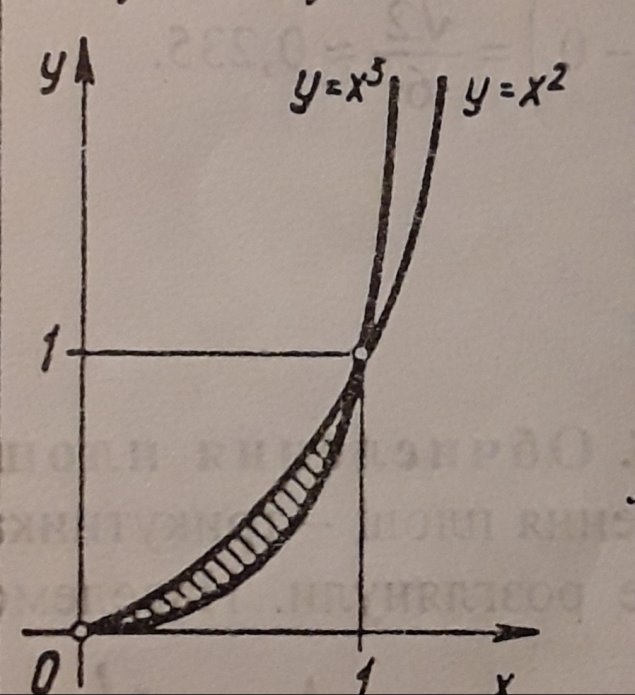
- Систематизація і узагальнення теоретичного матеріалу:
- загальний вигляд первісної
- задачі практичного змісту
- основна властивість первісної
- правила знаходження первісної
- поняття інтегралу
- формула Ньютона- Лейбніца
- властивості інтегралу
- застосування інтегралу
- площа плоскої фігури
- Підсумок уроку.
Сьогодні ми систематизували матеріал,що стосується розв’язання задач на знаходження площі плоских фігур. Учням пропонується відтворити відомості про нові цікаві факти уроку а також способи розв’язання прикладних задач.
Підбиваються підсумки виступу кожної групи, аналізується активність їх учасників, основні помилки і успіхи.
- Домашне завдання.
- П.5 ,стр.389,№1(а-г),№2(а-д)№10(а-д). Академічний рівень. А.Г.Мерзляк.
- Творче завдання. Знайти площу плоскої фігури з елементів вашого будинку.
про публікацію авторської розробки
Додати розробку