Презентація "Обдаровані діти"
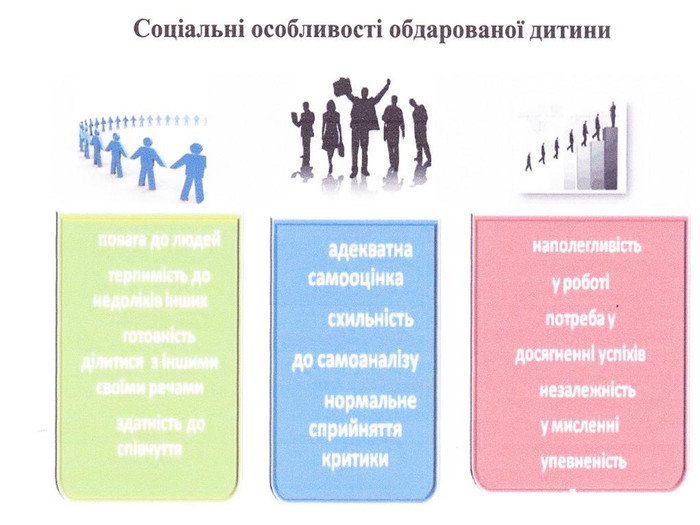
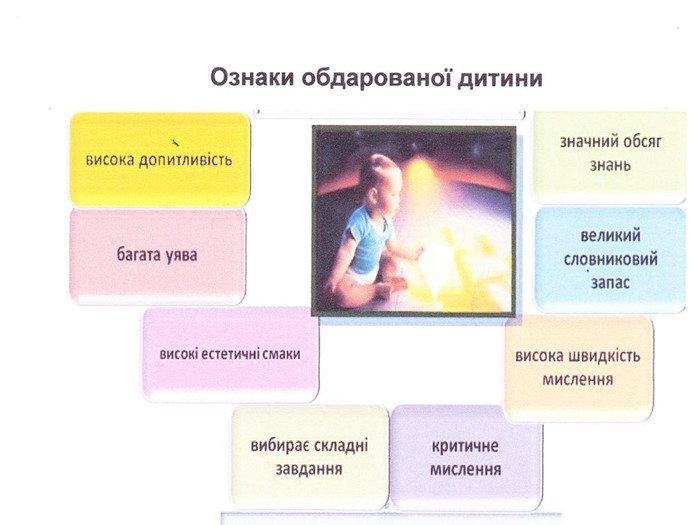
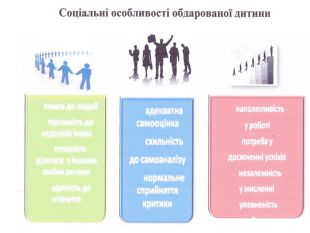
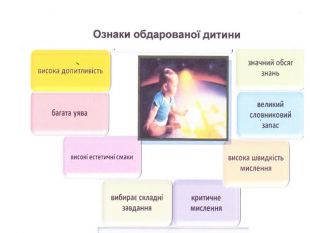
Обдаровані діти — це діти, які різко виділяються із середовища ровесників високим розумовим розвитком, що є наслідком як природних задатків, так і сприятливих умов виховання. Вони виявляють себе найбільш яскраво в таких сферах діяльності: інтелектуальній, академічних досягнень, творчості, комунікаціях та лідерстві, в різних видах діяльності і руховій сфері.
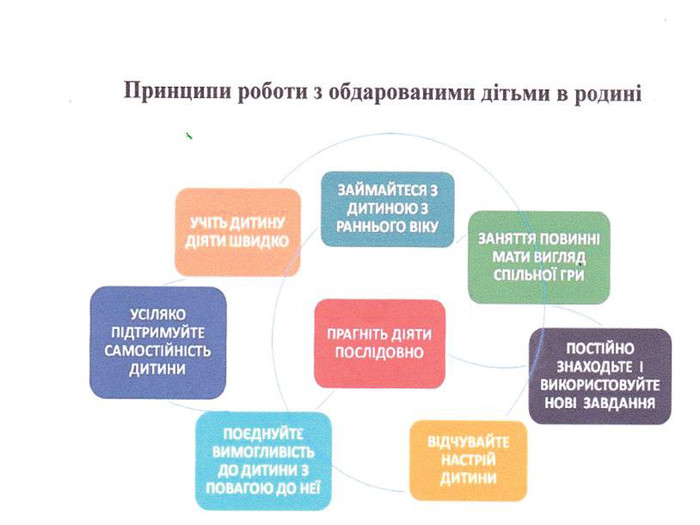
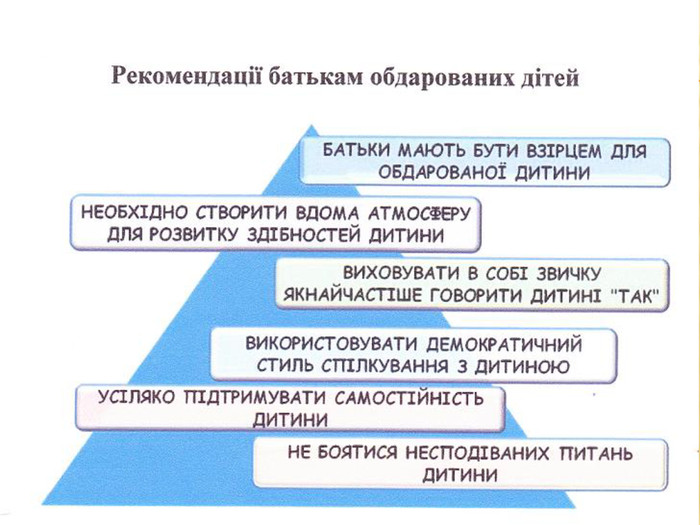
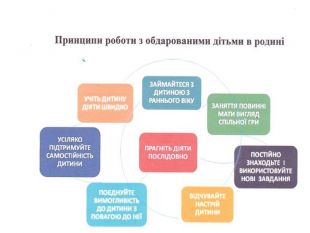
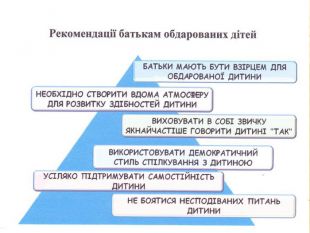
Як і батькам, вчителю для навчання обдарованих дітей необхідно знати їхні психологічні особливості, перейматися проблемами й інтересами; володіти здатністю їх розпізнавати, активізувати і розвивати, мати віру в учня, бути доброзичливим в оцінці дій учня, вміти поставити себе на місце дитини; бути фахівцем вищого ґатунку — володіти предметними психолого-педагогічними і методичними знаннями; мати високий рівень інтелекту, широку ерудицію. Він також має постійно самовдосконалюватись, вчити і вчитись сам: бути ентузіастом, цілеспрямованим, наполегливим, впевненим у своїх силах, принциповим у важливих питаннях і водночас гнучким, коли йдеться про другорядне. Як відомо, лише особистість може виховати особистість і тільки талант може виростити талант.


про публікацію авторської розробки
Додати розробку