Презентація " Основи теорії ймовірностей"
Про матеріал
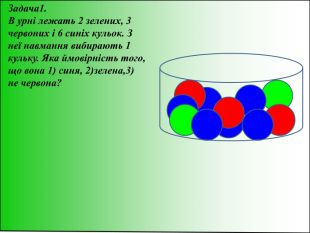
Мета: Ознайомити учнів з поняттями: випробовування, випадкова подія, повна група подій, видами подій Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку