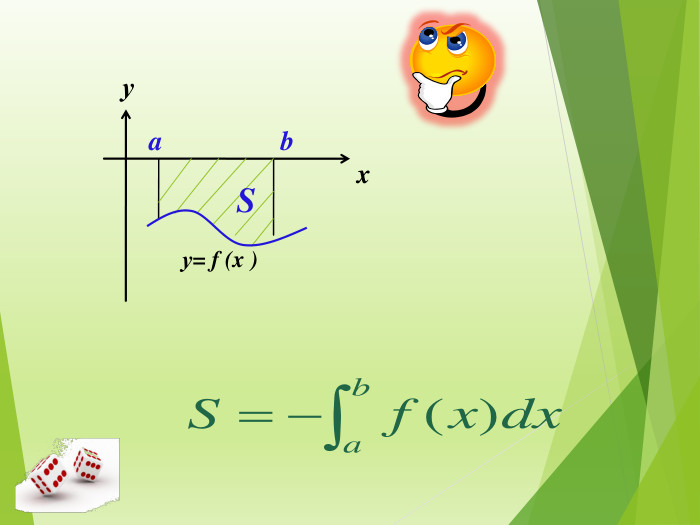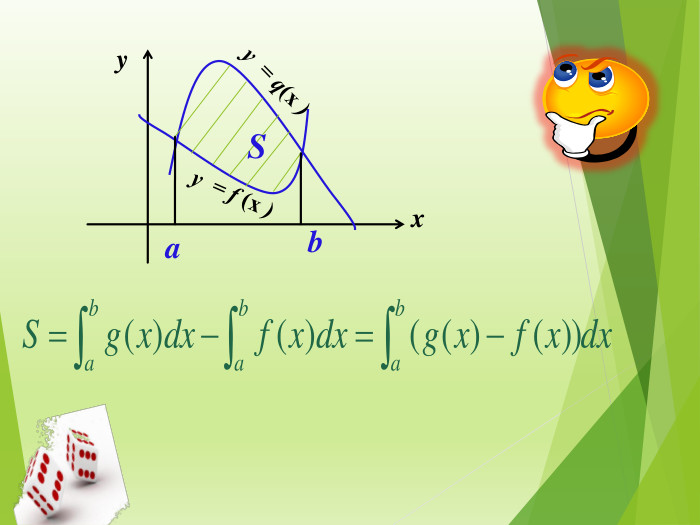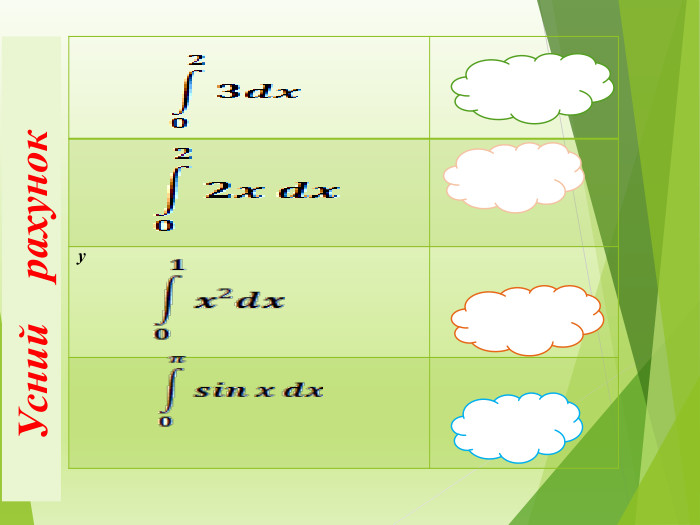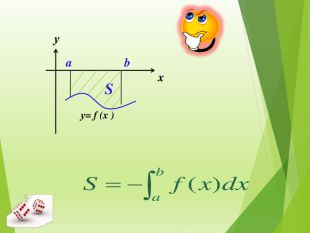Презентація "Визначений інтеграл"
Про матеріал
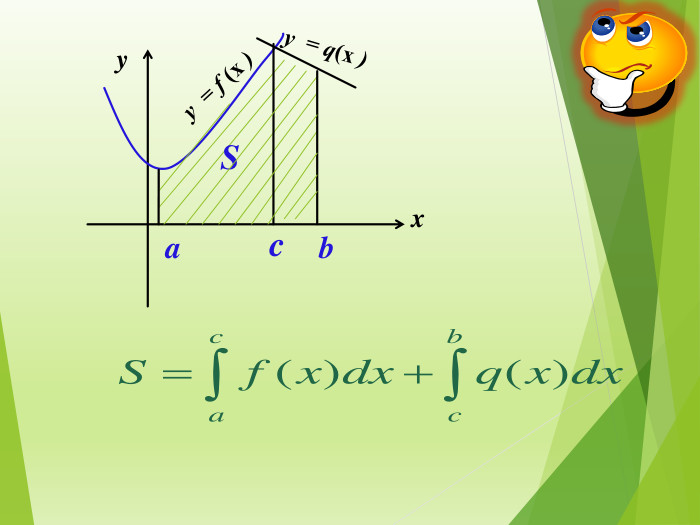
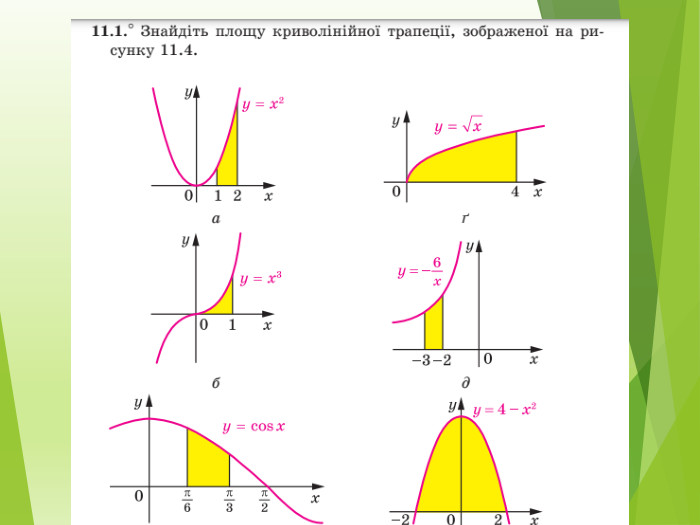
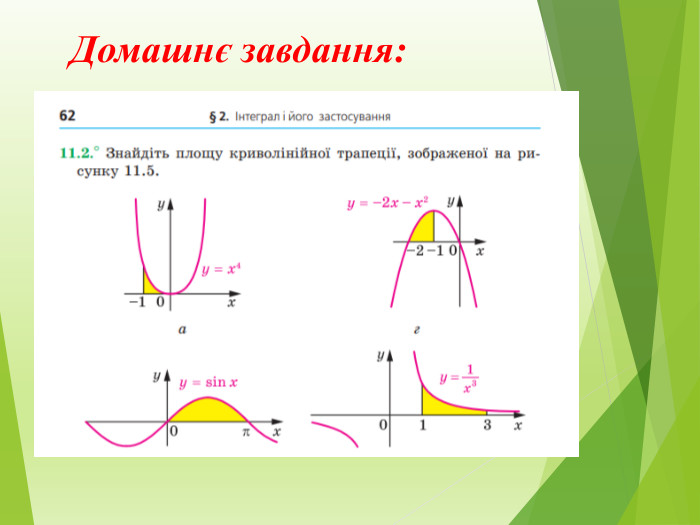
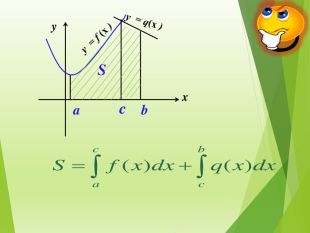
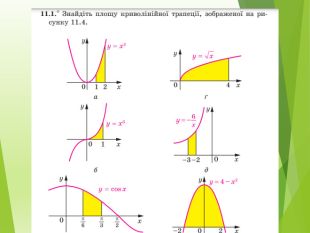
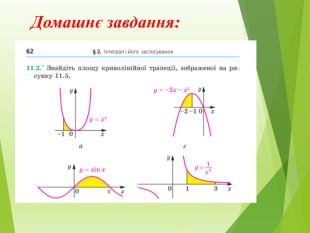
Публікація знайомить із застосуванням визначеного інтеграла до обчислення площі криволінійної трапеції різних видів Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


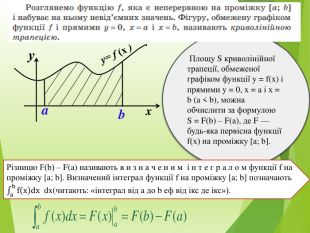
![Площу S криволінійної трапеції, обмеженої графіком функції y = f(x) і прямими y = 0, x = a і x = b (a < b), можна обчислити за формулою S = F(b) – F(a), де F — будь-яка первісна функції f(х) на проміжку [a; b]. у= f (x )уxab. Різницю F(b) – F(a) називають в и з н а ч е н и м і н т е г р а л о м функції f на проміжку [a; b]. Визначений інтеграл функції f на проміжку [a; b] позначають abfxdx dx(читають: «інтеграл від a до b еф від ікс де ікс»). Площу S криволінійної трапеції, обмеженої графіком функції y = f(x) і прямими y = 0, x = a і x = b (a < b), можна обчислити за формулою S = F(b) – F(a), де F — будь-яка первісна функції f(х) на проміжку [a; b]. у= f (x )уxab. Різницю F(b) – F(a) називають в и з н а ч е н и м і н т е г р а л о м функції f на проміжку [a; b]. Визначений інтеграл функції f на проміжку [a; b] позначають abfxdx dx(читають: «інтеграл від a до b еф від ікс де ікс»).](/uploads/files/4918377/424389/480052_images/2.jpg)