Презентація "Перестановки, розміщення, комбінації"

Презентація. Тема уроку “Елементи комбінаторики. Перестановки, розміщення, комбінації”Вчитель математики Тульчинської школи-ліцею. Кузик Тамари Іванівни

Мета Уроку: Ознайомити ліцеїстів з новим розділом математики;дати означення факторіала, перестановки, розміщення, комбінації без повторень; розглянути задачі з використанням формул для обчислення кількості різних сполук; розглядання правил суми і добутку; сформувати вміння знаходити значення і перетворювати вирази з факторіалами, застосовувати правила комбінаторики при розв'язуванні задач;розвивати увагу і пам’ять;виховувати впевненість в своїх силах, колективізм і самостійність, зацікавленість предмету.

*уміння вчитися впродовж життя;*математичну компетентність;*ініціативність та підприємливість;*соціально - громадянську компетентність. Формування компетентностей:

Хід уроку.

Організаційна частина*Описати психологічний стан особистостей

Актуалізація опорних знань

ПОВТОРЕННЯ матеріалу до ЗНО Множина може містити будь-яку кількість елементів. Якщо множина містить скінчене число елементів, то вона називається скінченною множиною. Якщо ж число елементів множини нескінчене, то і множина називається нескінченною. Якщо множина не містить жодного елемента, то таку множину називають порожньою і позначається Ø . Якщо множини складаються з одних і тих же елементів, то такі множини називаються рівними. Наприклад: {12; 13; 14; 15} = {15; 14; 13; 12}.

Пояснення нового матеріалу

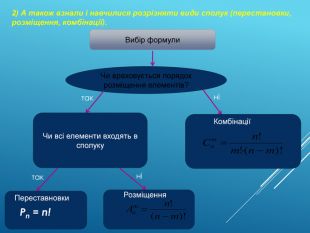
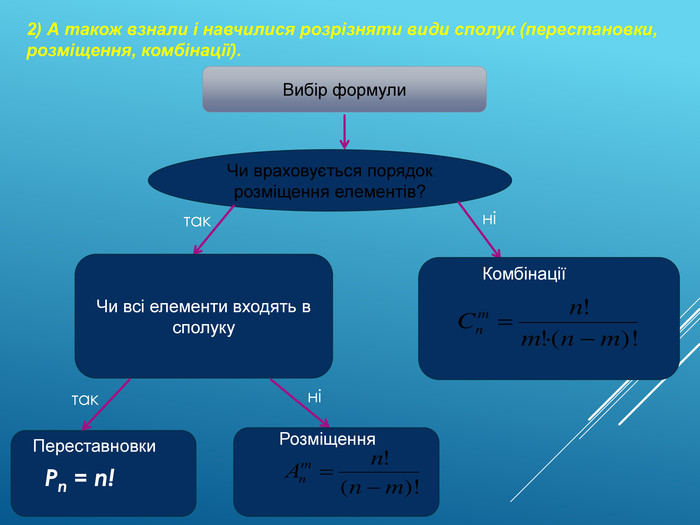
ПЛАН: Комбінаторика: Зміст матеріалу Приклади Основні формули комбінаторики: Факторіал Виконання вправ. Перестановки, приклади Виконання вправ. Розміщення , приклад1, приклад2 Виконання вправ. Комбінації, приклад Виконання вправ Основні закони комбінаторики: Зміст матеріалу Приклади Виконання вправ Домашнє завдання Підсумок заняття. Схема (вибір сполук)Схема (два основні правила комбівнаторики)

Історія виникнення поняття. Термін «комбінаторика» був введений в математичний ужиток Лейбніцем, який в 1666 році опублікував свою працю «Міркування про комбінаторне мистецтво». Готфрід Вільгельм Лейбніц (Gottfried Wilhelm von Leibniz)  - німецький філософ, математик, механік, юрист, дипломат.

Комбінаторика – важливий розділ математики, знання якого необхідно представникам різноманітних спеціальностей. З комбінаторними задачами доводиться мати справу фізикам, хімікам, біологам, лінгвістам, спеціалістам по кодам та ін. Комбінаторні методи лежать в основі рішення багатьох задач теорії ймовірностей та її застосувань. Методи розв'язування таких задач вивчають у розділі математики, який називається комбінаторикою, а самі задачі — комбінаторними.

Приклади комбінаторних задач: Дізнатися, скількома способами можна з 6 хлопчиків і 8 дівчаток вибрати команду для естафети, якщо в команду повинні увійти 3 хлопчика і 3 дівчинки. Скількома способами можуть бути розподілені золота і срібна медалі за підсумками олімпіади, якщо число команд 15?

Факторіал. Означення 1. Факторіал — це добуток послідовних натуральних чисел. n! = 1 ∙ 2 ∙ 3 ∙ ... ∙ n. Наприклад : 1! = 1; 2! = 1 ∙ 2 = 2; 3! = 1 ∙ 2 ∙ 3 = 6; 4! = 1 ∙ 2 ∙ 3 ∙ 4 = 3! ∙ 4 = 24. Приймають, що 0! = 1. Термін «факторіал» походить від англійського слова «фактор» — множник.

ПРиклади1) Обчислити: 2) Спростити:

Перестановки. Рn = n!

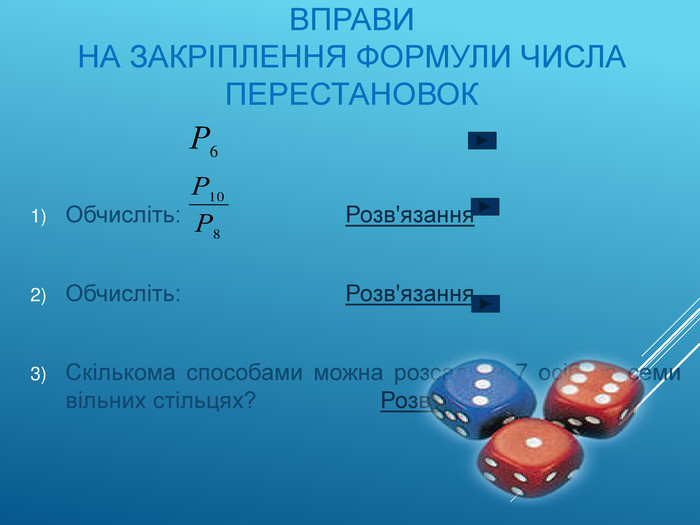
Перестановки. Означення 2. Будь-яка впорядкована множина, що складається з n елементів, називається перестановкою з n елементів. Перестановки відрізняються одна від одної лише порядком елементів. Приклад 1. Із елементів множини А = {2, 4, 5} можна утворити 6 перестановок: {2, 4, 5}, {2, 5, 4}, {4, 2, 5}, {4, 5, 2}, {5, 4, 2}, {5, 2, 4}. Кількість усіх можливих перестановок у множині з n елементів позначається Рn. Обчислюється за формулою: Рn = n!Приклад 2. 12 осіб можна розмістити за столом, біля якого поставлено 12 стільців, РІ2= 12! способами.

Вправина закріплення формули числа перестановок. Обчисліть: Розв'язання. Обчисліть: Розв'язання. Скількома способами можна розсадити 7 осіб на семи вільних стільцях? Розв'язання

Розв'язання. Обчисліть:

Розв'язання. Обчисліть:

Розв'язання. Скількома способами можна розсадити 7 осіб на семи вільних стільцях? Щоб обчислити скільки способів існує для того щоб розсадити 7 осіб на семи вільних стільцях треба знайти число перестановок :

Перестановки. Будь-яка впорядкована множина, яка складається з заданих n-елементів, називається перестановкою із n-елементів. Позначають через Р – перша буква французького слова «permutation» – «перестановки»   𝑷𝒏=𝒏!Приклад 9. Скількома способами можна розставити на полиці 6 книжок?Розв’язання. Шукана кількість способів дорівнює кількості перестановок з 6 елементів (книг): Р6 = 6! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720. Приклад 10. Скільки різних чотирицифрових чисел можна скласти з цифр 0; 1; 2; 3, якщо в кожному числі жодна з цифр не повторюється?Розв’язання. З чотирьох цифр 0; 1; 2; 3 можна утворити Р4 перестановок. Але ті перестановки, які починаються з 0 не будуть записами чотирицифрових чисел, таких перестановок — Р3. Отже, шукана кількість чотирицифрових чисел дорівнює Р4 - Р3 = 4! - 3! = 3!(4 - 1) = 6 ∙ 3 = 18. 

Розміщення

розміщення. Означення 3. Упорядкована підмножина з m елементів даної множини М, що містить n елементів, де m ≤ n, називається розміщенням з n елементів по m. Розміщення відрізняються один від одного або елементами, або їх порядком. Якщо m = n, маємо перестановку з n елементів, тобто перестановка є окремим випадком розміщення за умови, що m = n. Кількість усіх можливих розміщень з n елементів по m елементів позначається 𝐴𝑛𝑚. Обчислюється за формулою: Приклад 1: Скільки двоцифрових чисел можна скласти з цифр 3, 5, 7. Розглянемо множину цифр{3, 5, 7} і випишемо розміщення з еле­ментів даної множини по два: 35, 53, 57, 75, 37, 73. 

Формула для обчислення кількості розміщень. Приклад 2. Студенту потрібно скласти 4 іспити на протязі 8 днів. Скількома способами це можна зробити Розв'язання:

Розв’язування задач. Приклад 3. Скількома способами можна розсадити 4 учні на 25 стільцях? Відповідь: = 303 600.

Приклад 4. Обчисліть:

Приклад 5. Обчисліть:

Приклад 6. Розв'яжіть рівняння: Розв'язати рівняння означає знайти змінну x. Тобто тоді Отже враховуюче, що x – натуральне число, отримаємо x=1. Відповідь: 1

Приклад 7. Кожен вибір трьох медалістів з 10 учасників відрізняється один від одного складом і порядком розташування учасників, тоді треба обчислити число розміщень з 10 по 3:

Комбінації

комбінаціїБудь-яка не упорядкована підмножина з m елементів даної множини М, що містить n елементів, де m ≤ n, називається комбінацією з n елементів по m. Порядок елементів у множині неістотний, комбінації відрізняються лише складом елементів. Кількість усіх можливих комбінацій з n елементів по m позначається символом Комбінація відрізняється від розміщення тим, що у цій підмножині неістотним є порядок елементів. У загальному випадку кількість комбінацій з n елементів по m елементів можна обчислити за формулою:

Формула для обчислення кількості комбінацій

Розв’язування задач. Приклад1: Скількома різними способами можна вибрати з 15 осіб делегацію в складі 3 осіб? Розв'язання: Різними вважатимемо ті делегації, які відрізняються хоча б однією особою. Отже, треба обчислити Відповідь. Існує 455 способів.

Приклад 9. Обчисліть:

Приклад 10. Обчисліть:

Приклад 11. Скільки прямих можна провести через 7 точок, з яких ніякі три не лежать на одній прямій? Кожні дві точки визначають одну пряму, і при цьому не відіграє ролі в якому порядку вони взяті. Тому число прямих дорівнює числу комбінацій з 7 по 2, тобто

*Приклад 12.. У вазі 6 червоних і 4 білих троянди. Скількома способами з вази можна вибрати: 1) три троянди; 2) дві червоні і одну білу троянду?Розв’язання. 1) Оскільки порядок вибору не має значення, то вибрати три троянди з 10 можна С310 способами.𝐶103=10!3!10−3!=7!∙8∙9∙103!∙7!=8∙9∙101∙2∙3=120 (способів)2) Дві червоні троянди можна вибрати С26 способами, а одну білу – C14 способами. Тому вибрати дві червоні і одну білу троянди можна способами. Маємо𝐶62∙𝐶41=6!2!6−2!∙4!1!4−1!=4!∙5∙62!∙4!∙3!∙43!=15∙4=60(способів) 

Приклад 13. Скількома способами можна закреслити 6 номерів із 49 в картці “Спортлото”Розв'язання:

Вибір формули 𝑨𝒏𝒌 чи 𝑪𝒏𝒌.  Якщо в комбінаторній задачі необхідно вибрати k елементів з n, то важливим є питання – необхідно враховувати порядок слідування елементів чи ні.{B301 B821-A1 FF-4177-AEE7-76 D212191 A09}В класі 20 учнів. Скількома способами з цього класу можна вибрати...старосту й його заступникадвох чергових. Обов’язки різні! Порядок має значення.𝐴202=20!18!=19∙20=380 Обов’язки однакові! Порядок не має значення. 𝐶202=20!2!∙18!=19∙202=190{B301 B821-A1 FF-4177-AEE7-76 D212191 A09}В класі 20 учнів. Скількома способами з цього класу можна вибрати...старосту й його заступникадвох чергових

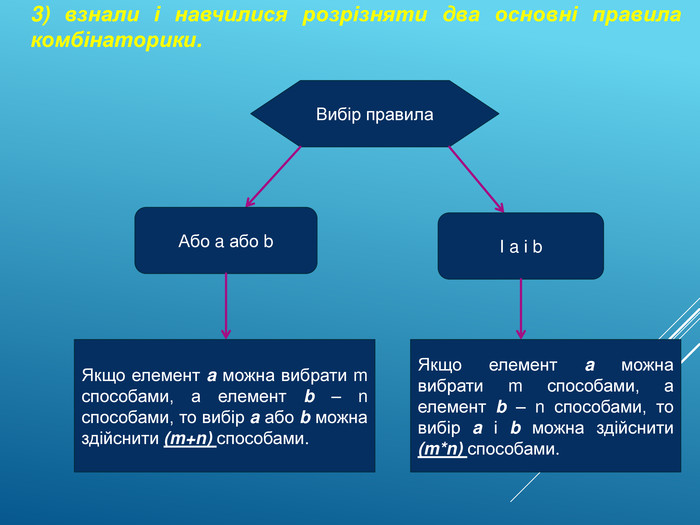
Правила суми і добутку. Комбінаторні задачі бувають різних видів. Але більшість із них розв'язують за допомогою двох основних правил: правила суми і правила добутку. Вибір правила. Правило суми: Або елемент a або елемент b. Якщо елемент a можна вибрати m способами, а елемент b – n способами, то вибір a або b можна здійснити (m+n) способами. Правило добутку:І елемент a і елемент b. Якщо елемент a можна вибрати m способами, а елемент b – n способами, то вибір a і b можна здійснити (m*n) способами.

Приклад 14.7 книг різних авторів і трьохтомник одного автора розташо­вані на книжковій полиці. Скількома способами можна роз­ставити ці 10 книжок на полиці так, щоб книги автора трьохтомника стояли поруч?

Приклад 16. Збори з 30 осіб обирають голову, секретаря та трьох членів редакційної комісії. Скількома способами це можна зробити?

Приклад 17. У підрозділі 60 солдат і 5 офіцерів. Скількома способами мож­на виділити наряд, який складається із трьох солдат і одно­го офіцера?

Підведення підсумків.

Приклади. Приклад 1: У групі 9 дівчаток і 11 хлопців. Скількома способами можна вибрати 1 студента для роботи біля дошки?Розв'язання: Для роботи біля дошки ми можемо вибрати дівчинку 9 способами або хлопця 11 способами.     Загальна кількість способів дорівнює 9 + 11 = 20. Приклад 2: На вершину гори ведуть 5 доріг. Скількома способами можна піднятися на гору і спуститися з неї?Розв'язання : Для кожного варіанту підйому на гору існує 5 варіантів спуску з гори. Значить всіх способів піднятися на гору і спуститися з неї 5 ∙ 5 = 25.

Вибір формули. Чи враховується порядок розміщення елементів?такніЧи всі елементи входять в сполуку. КомбінаціїтакніПереставновки. Рn = n!Розміщення2) А також взнали і навчилися розрізняти види сполук (перестановки, розміщення, комбінації).

3) взнали і навчилися розрізняти два основні правила комбінаторики. Вибір правила. Або a або bІ a і b. Якщо елемент a можна вибрати m способами, а елемент b – n способами, то вибір a або b можна здійснити (m+n) способами. Якщо елемент a можна вибрати m способами, а елемент b – n способами, то вибір a і b можна здійснити (m*n) способами.

Домашнє завдання Дедалі частіше в житті приходиться розв'язувати задачі, головним питанням у яких є: «Скількома способами це можна зробити?»Наприклад:• Скільки прямих можна провести через 7 точок, з яких ніякі три не лежать на одній прямій? • Скількома способами можуть бути присуджені золота, срібна або бронзова медалі трьом учасникам з 10?• Скількома способами можна розсадити 7 осіб на семи вільних стільцях? У цих задачах задано елементи для комбінування і вимагається знайти кількість можливих комбінацій.І саме такі задачі отримали назву: комбінаторні задачі. А розділ математики, в якому розглядаються подібні задачі, називають комбінаторикою?Прошу розв’язати дані задачі

Рефлексія

МОЛОДЦІ!