Презентація "Підмножини"

Лекція. Основні поняття ТЕОРІЇ МНОЖИН (2)Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

План. Порожня множина. Універсальна множина. Рівність множин. Підмножини. Булеан. Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

Порожня множина. Порожня множина – це множина, що не містить елементів. Цей об'єкт за визначенням має такі властивості: Він є множиною;Ця множина не має жодного елементу;Ця множина єдина. Позначається порожня множина . Приклади порожніх множин: {x| x – ціле число, яке ділиться на 4, але не ділиться на 2};{x| x – людина, ріст якої більше 5 м};{x| x – місто, кількість населення якого більше 1 млрд. };{x| xZ  0

ВПРАВИЯкі з даних множин є порожніми?1. {x| xZ+, 24x<30  х - просте число} (відповідь – непорожня, оскільки число 29 є елементом множини).2. {x| xZ+, 47

ВПРАВИЯкі з даних множин є порожніми?1. {x| xZ+, 24x<30  х - просте число} (відповідь – непорожня, оскільки число 29 є елементом множини).2. {x| xZ+, 47

Універсальна множина. Назвемо основною або фундаментальною множиною множину, що створена всіма елементами будь-якого визначеного типу. Позначимо її буквою V- читається "універсум" або "універсальна множина". Наприклад: V= {х|х- довільна точка площини ХОУ},V= {х | х- прямі на площині};V= {х | х- зірка на небі}. Універсальна множина U містить всі можливі елементи, що зустрічаються в даній задачі. Універсальна множина U визначається конкретно для кожної окремої задачі відповідно її умов. Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

Рівність множин Якщо потрібно записати, що два різних символи позначають одну і ту ж множину, то між символами ставлять знак рівності. Наприклад:{x| x – натуральне парне просте число}={2};{x| xZ+, x<10  х - просте число}={2,3,5,7};{x| xQ  |x|= -1}=. Отже, якщо А і В – множини, то рівність А=В означає, що А і В – одна і та ж множина, тобто, що кожен елемент множини А є одночасно елементом множини В і навпаки, кожен елемент множини В є елементом множини А:(A=B)[(xA)  (xB)]  [ (xB)  (xA)] або A=BAB& BAНовокаховський приладобудівний технікум. Викладач Біляєва Г. М.

ВПРАВИЧи правильне твердження?1. 2. Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

підмножини. Якщо AB та АВ, то А називається власною підмножиною В. Підмножиною будь-якої множини М є сама ця множина і також порожня множина . Це витікає з визначення підмножини:а) якщо хМ, то з хМ, виходить, що ММ.б) будь-який елемент порожньої множини  є елементом множини М, оскільки порожня множина  не має елементів, отже, М. Інші підмножини множини М (якщо вони існують) містять деякі (але не всі) елементи цієї множини. Порожня множина  має тільки одну підмножину . Множина М, яка має тільки один елемент |М|=1 – має вже дві підмножини -  і М. Трьохелементна множина M={а,b,c} матиме такі підмножини : ,{a}, {b}, {c}, {а,b},{а, с},{b,c}, {а,b,c}. Новокаховський приладобудівний технікум. Викладач Біляєва Г. М. Якщо всі елементи деякої множини А входять до складу множини В, то множина А називається підмножиною множини В: AB, тобто множина А міститься у В, а множина В включає множину А. Отже (AB) (xA)  (xB). В цьому випадку А – підмножина В, а В – надмножина А.

підмножини. Новокаховський приладобудівний технікум. Викладач Біляєва Г. М. Властивості операції включення:1. Якщо AB та BС AС 2. Якщо AB та BA A=B {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Множина АПотужність множини. Підмножини. Кількість підмножин|A|=0|(A)|=120{1}|A|=1, {1}|(A)|=221{1,2}|A|=2, {1}, {2}, {1,2}|(A)|=422{1,2,3}|A|=3, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}|(A)|=823{1,2,3,4}|A|=4, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}|(A)|=1624?

підмножини. Новокаховський приладобудівний технікум. Викладач Біляєва Г. М. Властивості операції включення:1. Якщо AB та BС AС 2. Якщо AB та BA A=B {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Множина АПотужність множини. Підмножини. Кількість підмножин|A|=0|(A)|=120{1}|A|=1, {1}|(A)|=221{1,2}|A|=2, {1}, {2}, {1,2}|(A)|=422{1,2,3}|A|=3, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}|(A)|=823{1,2,3,4}|A|=4, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}|(A)|=1624

булеан. Булеан (англ. power set) — в теорії множин, це множина всіх підмножин даної множини A, позначається  (A ) або 2|A|Новокаховський приладобудівний технікум. Викладач Біляєва Г. М. |A|=n , |(A)|=2n

ВПРАВИІ. Визначити, які з даних пар множин рівні між собою?Множина всіх точок даної площі і множина всіх прямих цієї самої площі? {x | x Z & 9х2<27} та {x | x Z & 6х229} ?{x | |x|<0} та {x | |x|0} ? та {}?Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

ВПРАВИІІ. Які з приведених тверджень правильні, а які ні:1. [AB  (BC)](AC)2. [AB  (BA)](A=B) 3. [AB  (BC)  (CA)  (AC)](A=B=C)4. [AB  (BC)]  (AC).5. [AB  (BC)]  (AC).ІІІ . Випишіть всі підмножини множини А={а,b}Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

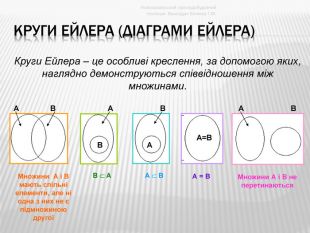
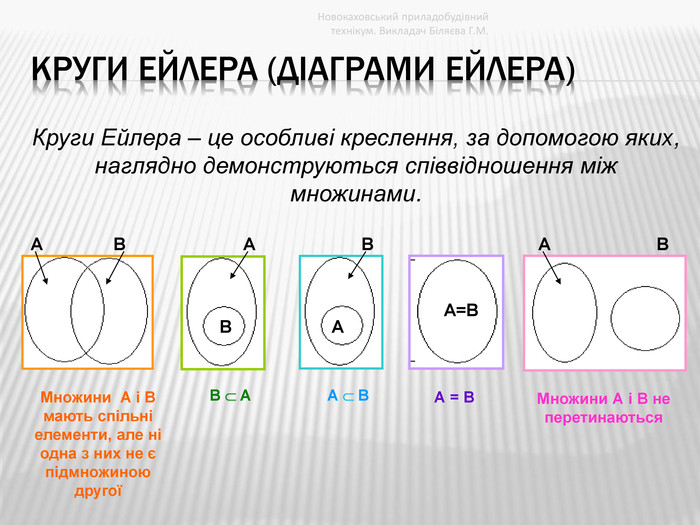
Круги Ейлера (діаграми ейлера) Новокаховський приладобудівний технікум. Викладач Біляєва Г. М. Круги Ейлера – це особливі креслення, за допомогою яких, наглядно демонструються співвідношення між множинами. АВАААВВВА=ВМножини А і В мають спільні елементи, але ні одна з них не є підмножиною другої В  АА  ВА = ВМножини А і В не перетинаютьсяstyle.colorfillcolorfill.type

ВПРАВИВизначити: правильно чи ні?1{{1,2,3}}; {3}{{1},{2},3}; {1,3}{{1},{2},{3}}{2}{1,2,3}; {1,3}{{1,3}}; {2}{{1},{2},{3}}3{{1,2,3}}; {3}{{1},{2},{3}}; 1{{1},{2},{3}}1{1,{2,3}}; {1,2}{{1,2}}; {1,2}{{1}, {2}, {3}}{2}{1,2,3}; 2{{1},{2},{3}}; {1,2}{{1}, {2}, {3}}Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

ВПРАВИВизначити: правильно чи ні?2{{1,2,3}}; {1,2}{{1,2}}; 3{{1}, {2}, {3}}3{{1,2,3}}; {2}{{1},{2},{3}}; {2,3}{1,2,3}{2}{1,2,3}; {1,2}{{1,2}}; {1,2}{{1},{1,2},3}{3}{1,2,3}; {3}{{1},{2},{3}}; {1,{3}}{1,2,{3}}2{1,2,3}}; {1,2}{1,2,{3}}, {2,3}{{1},{2},{3}}Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

ВПРАВИВизначити: правильно чи ні?1{{1,2,3}}; {3}{{1},{2},3}; {1,3}{{1},{2},{3}}{2}{1,2,3}; {1,3}{{1,3}}; {2}{{1},{2},{3}}3{{1,2,3}}; {3}{{1},{2},{3}}; 1{{1},{2},{3}}1{1,{2,3}}; {1,2}{{1,2}}; {1,2}{{1}, {2}, {3}}{2}{1,2,3}; 2{{1},{2},{3}}; {1,2}{{1}, {2}, {3}}Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

ВПРАВИВизначити: правильно чи ні?2{{1,2,3}}; {1,2}{{1,2}}; 3{{1}, {2}, {3}}3{{1,2,3}}, {2}{{1},{2},{3}}; {2,3}{1,2,3}{2}{1,2,3}; {1,2}{{1,2}}; {1,2}{{1},{1,2},3}{3}{1,2,3}; {3}{{1},{2},{3}}; {1,{3}}{1,2,{3}}2{{1,2,3}}; {1,2}{1,2,{3}}; {2,3}{{1},{2},{3}}Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

ВПРАВИНовокаховський приладобудівний технікум. Викладач Біляєва Г. М. Розмістити дані множини у такій послідовності, щоб кожна наступна множина була підмножиною попередньої: І варіант. Z- множина цілих чисел;Q- множина раціональних чисел;R- множина дійсних чисел;N- множина натуральних чисел;P- множина додатних чисел, які діляться на 5.ІІ варіант. A - множина чотирикутників;K - множина квадратів;P - множина паралелограмів;R - множина ромбів;M - множина многокутників. QRPN ZPRKAMP N  Z  Q  RK  R  P  A  M??

ВПРАВИНовокаховський приладобудівний технікум. Викладач Біляєва Г. М. Розмістити дані множини у такій послідовності, щоб кожна наступна множина була підмножиною попередньої: І варіант. Z- множина цілих чисел;Q- множина раціональних чисел;R- множина дійсних чисел;N- множина натуральних чисел;P- множина додатних чисел, які діляться на 5.ІІ варіант. A - множина чотирикутників;K - множина квадратів;P - множина паралелограмів;R - множина ромбів;M - множина многокутників. QRPN ZPRKAMP N  Z  Q  RK  R  P  A  M

Повторення. Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.

Д/3 М. Ф. Бондаренко, Н. В. Білоус, А. Г. Руткас , «Комп’ютерна дискретна математика», Харків, «Компанія СМІТ», 2004р.1. стор. 17 вправи № 2, 4, 6.2. стор. 20 вправи № 1-3 Новокаховський приладобудівний технікум. Викладач Біляєва Г. М.