Презентація "Початки теорії ймовірностей. Урок 1."
Архів містить презентацію «Початки теорії ймовірностей» та текстові файли для гіперпосилань на додаткову інформацію до презентації.
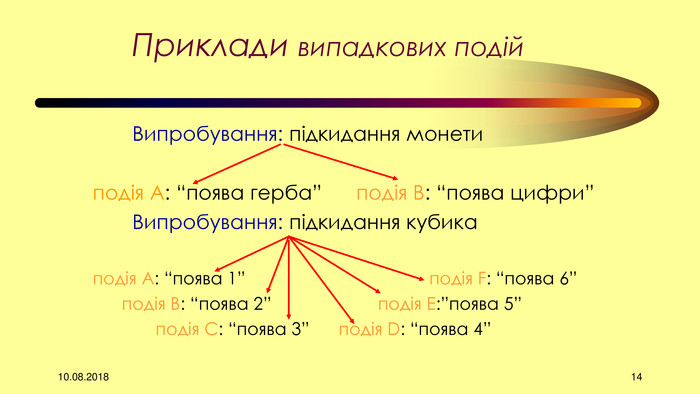
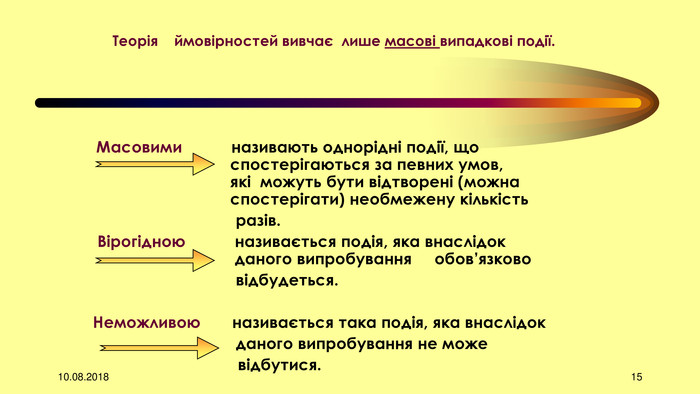
Презентація складається з вступної частини до теми «Елементи теорії ймовірностей» для учнів 11 класу та уроку № 1 з 12 уроків циклу.. Матеріал може бути використаний вчителями на уроці в повному обсязі чи в скороченому вигляді, залежно від рівня викладання предмету.
- êâÉ¢.doc doc
- îàÆàÄÉêÆ.doc doc
- .doc doc
- .ô᫬ 1.pptx pptx
- Показати всі файли
ПАСКАЛЬ (Pascal) Блез (1623-62),
французский математик, физик, религиозный философ и писатель. Сформулировал одну из основных теорем проективной геометрии. Работы по арифметике, теории чисел, алгебре, теории вероятностей. Сконструировал (1641, по другим сведениям — 1642) суммирующую машину. Один из основоположников гидростатики, установил ее основной закон (см. Паскаля закон). Работы по теории воздушного давления. Сблизившись с представителями янсенизма, с 1655 вел полумонашеский образ жизни. Полемика с иезуитами отразилась в «Письмах к провинциалу» (1656-57) — шедевре французской сатирической прозы. В «Мыслях» (опубликованы в 1669) Паскаль развивает представление о трагичности и хрупкости человека, находящегося между двумя безднами — бесконечностью и ничтожеством (человек — «мыслящий тростник»). Путь постижения тайн бытия и спасения человека от отчаяния видел в христианстве. Сыграл значительную роль в формировании французской классической прозы.
ПАСКАЛЬ (Pascal) Блез (1623-62),
французский математик, физик, религиозный философ и писатель. Сформулировал одну из основных теорем проективной геометрии. Работы по арифметике, теории чисел, алгебре, теории вероятностей. Сконструировал (1641, по другим сведениям — 1642) суммирующую машину. Один из основоположников гидростатики, установил ее основной закон (см. Паскаля закон). Работы по теории воздушного давления. Сблизившись с представителями янсенизма, с 1655 вел полумонашеский образ жизни. Полемика с иезуитами отразилась в «Письмах к провинциалу» (1656-57) — шедевре французской сатирической прозы. В «Мыслях» (опубликованы в 1669) Паскаль развивает представление о трагичности и хрупкости человека, находящегося между двумя безднами — бесконечностью и ничтожеством (человек — «мыслящий тростник»). Путь постижения тайн бытия и спасения человека от отчаяния видел в христианстве. Сыграл значительную роль в формировании французской классической прозы.
ПАСКАЛЬ (Pascal) Блез (1623-62),
французский математик, физик, религиозный философ и писатель. Сформулировал одну из основных теорем проективной геометрии. Работы по арифметике, теории чисел, алгебре, теории вероятностей. Сконструировал (1641, по другим сведениям — 1642) суммирующую машину. Один из основоположников гидростатики, установил ее основной закон (см. Паскаля закон). Работы по теории воздушного давления. Сблизившись с представителями янсенизма, с 1655 вел полумонашеский образ жизни. Полемика с иезуитами отразилась в «Письмах к провинциалу» (1656-57) — шедевре французской сатирической прозы. В «Мыслях» (опубликованы в 1669) Паскаль развивает представление о трагичности и хрупкости человека, находящегося между двумя безднами — бесконечностью и ничтожеством (человек — «мыслящий тростник»). Путь постижения тайн бытия и спасения человека от отчаяния видел в христианстве. Сыграл значительную роль в формировании французской классической прозы.
Ферма (Пьер Fеrmat)
— знаменитый французский математик 1601 — 65). Сын торговца; изучил законоведение и с 1631 г. до конца жизни был советником Тулузского парламента. Научные сведения Ф., и притом не только в области наук математических, поражали его соотечественников разносторонностью. Владея южноевропейскими языками и глубоко изучив латинский и греческий, Ф. был гуманистом и поэтом, писавшим французские и латинские стихи. Из древних писателей он комментировал Атенея, Полиенуса, Синезиуса, Теона Смирнского и Фронтина, исправил текст Секста Эмпирика. Изучив творения Бэкона Веруламского, он не только проник в их смысл глубже Декарта, но в отношении экспериментального метода он пошел даже далее самого их автора, так как не ограничился одним теоретическим знакомством с методом, но в ряде опытов по предмету экспериментальной механики дал ему непосредственное приложение к действительности. При жизни Ф. об его математических работах стало известно главным образом через посредство обширной переписки, которую он вел с другими учеными, преимущественно с Мерсеннем, Робервалем, Паскалями, Этьенном и Блезом, Декартом, Френиклем, Каркави, Гассенди, Сенье, Булльо, Дигби, Клерселье, Лалувером и Гюйгенсом. Сам Ф. напечатал только два свои произведения: геометрическую диссертацию «De linearum curvarum cum lineis rectis comparatione» (Тулуза, 1660), вместе с приложением к ней и анонимную статью без заглавия, вошедшую в качестве «первой части второго прибавления» в состав книги иезуита Лалувера: «Veterum Greometria promota in septem de Cycloide libris, et in duabus adjectis Appendicibus» (Тулуза, 1660). Из переписки Ф. при его жизни в печать проникли, кроме нескольких отрывков, письмо к Гассенди, помешенное в VI томе «Собрания сочинений» последнего (Лион, 1658), и девять писем, напечатанных английским математиком Валлисом в его издании « Commtrcium epistolicum de Quaestionibus quibusdam Mathematicis nuper habitum inter nobilissimos Viros etc.» (Оксфорд, 1658). Этих работ Ф. оказалось, однако же, вполне достаточным для единогласного его признания современниками одним из выдающихся математиков. Крупную заслугу Ф. перед наукой видят, обыкновенно, во введении им бесконечно малой величины в аналитическую геометрию, подобно тому, как это несколько ранее, было сделано Кеплером в отношении геометрии древних. Он совершил этот важный шаг в своих относящихся к 1629 г. работах о наибольших и наименьших величинах, — работах, открывших собою тот из важнейших рядов исследований Ф., который является одним из самых крупных звеньев в истории развития не только высшего анализа вообще, но и анализа бесконечно малых в частности. Метод Ф. нахождения наибольших и наименьших величин состоял в следующем. В выражение, переходящее в свое наибольшее или наименьшее значение, вместо неизвестного х вставляется сумма двух неизвестных х+е. Полученная через эту подстановку новая форма выражения приравнивается его первоначальной форме, чем и порождается взгляд на неизвестное е, как на величину крайне малую. В найденном, таким образом, уравнении опускаются содержащиеся в обеих его частях одинаковые члены, оставшиеся делятся на е и те из них, в которых е удержалось и после деления, опускаются совсем. В результате получается уравнение, доставляющее наибольшее или наименьшее значение неизвестного х. В терминах современного знакоположения весь этот процесс может быть представлен в виде или,
или
Изложенный первоначально в статье «Methodus ad disquirendam maximum et minimam», этот метод лег в основание и двух следовавших за ним, также очень важных работ Ф. в той же области, именно способа проведения касательных к кривым и приема определения центра тяжести параболоида вращения. Из них первый сделался известным в 1642 г. из «Дополнения» к «Cursus mathematici» Геригона, а второй — из статьи «Centrum gravitatis parabolici conoidis, ex eadem methodo», пересланной в 1638 г. через Мерсення Робервалю. В ряде исследований Ф. по предмету высшего анализа все указанные до сих пор могут быть обозначены, следуя новейшей терминологии, одним общим названием приложений дифференциального исчисления. Что касается остальных исследований из принадлежащих тому же ряду, то они также могут быть соединены в одну группу, общая характеристика которой вполне исчерпывается термином приложения интегрального исчисления. Членами этой группы были квадратуры, кубатуры и ректификации. Первое сделавшееся известным изложение результатов работ Ф. по предмету квадратур и кубатур представляет упомянутая уже выше статья («Ad Bon. Cavalierii quaestiones responsa»), посланная автором в 1644 г. Кавальери через посредство Мерсення. Предмет ее состоит в несопровождаемом доказательствами изложении данных автором решений вопросов Кавальери. Она содержит в себе квадратуры парабол различных порядков, кубатуры происходящих от них тел вращения и определения центров тяжести последних. В гораздо более подробном виде знакомит с теми же работами Ф. другое, по-видимому, более позднее сочинение, напечатанное после смерти автора: «De aequationum localium transmutatione et emendatione ad multimodam curvilineorum inter se vel cum rectilineis comparationern, cui annectitur proportionis geometricae in quadrandis infinitis parabolis et hyperbolis usus». Что касается найденного Ф. способа ректификации или выпрямления кривых, то он изложен в его уже упомянутой выше диссертации «De linearum curvarum cum lineis rectis comparatione». Не менее важными по своим последствиям, чем работы по высшему анализу, и едва ли не более блестящими по своей глубине и остроумию были результаты исследований Ф. в области теории чисел. Особого, посвященного им сочинения автор не оставил, но сохранились заметки, рассеянные и, по большей части, без доказательств в письмах Ф., и в особенности на полях принадлежащего автору экземпляра сочинений Диофанта в издании Баше де Мезириака. В числе заметок на экземпляре сочинений Диофанта находилось важнейшее из открытий Ф. в области теории чисел, — теорема о невозможности разложения какой-нибудь степени, за единственным исключением квадрата, на две такие же степени. Знаменитое предложение, известное под именем теоремы Ф. и выражаемое сравнением (mod p), в котором р есть первоначальное число, а а есть число, не делящееся на р, было дано Ф. в письме к неизвестному лицу от 18 октября 1640 г. Доказательство первой из этих двух теорем было найдено позднейшими математиками (Эйлером, Дирикле, Куммером) только с большим трудом, и притом в формах, которыми сам Ф. никак не мог пользоваться. Из других работ Ф. остается упомянуть: 1) об его занятиях решением некоторых вопросов теории вероятностей, вызванных или поставленных перепискою с Блезом Паскалем; 2) о попытках восстановления некоторых из утраченных произведений древних греческих математиков и, наконец, 3) об его спорах с Декартом по поводу метода определения наибольших и наименьших величин и по вопросам диоптрики. Сочинениями, которые Ф. намеревался восстановить, были «Поризмы» Эвклида и «Плоские места» Аполлония Пергейского. Поводом ко второму из вышеупомянутых споров Ф. с Декартом был найденный последним закон преломления. Ф. находил сомнительным утверждение противника, что свет при прохождении через тело встречает тем менее сопротивления, чем это тело плотнее. Также спорил он и против утверждения, что отражение света может быть объяснено отскакиванием неупругих световых частиц. Позднее, после смерти Декарта, спор по тем же предметам Ф. продолжал с его учеником Kлepселье. Собрание математических сочинений и писем Ф. было издано в, первый раз его сыном Самюелем в 1679 г. : «Varia opera mathematica D. Petri de Fermat, Senatoris tolosani. Accesserunt selectae quaedam ejusdem Epistolae, vel ad ipsum a plerisque doctissimis viris Gallice, Latine, vel Italice, de rebus ad Mathematicis disciplinas aut Physicam pertinentibus scriptae» (Тулуза). В 1861 г. в Берлине появилась перепечатка этого издания, сделанная Фридлендером. Новое, более полное и совершенное собрание сочинений Ф. было издано в Париже в трех томах, под заглавием «Oeuvres de Fermat, publiees par les soins de P. Tannery et Ch. Henry» (1896).

про публікацію авторської розробки
Додати розробку