Презентація "Прямокутник, окремі види паралелограма"
Про матеріал
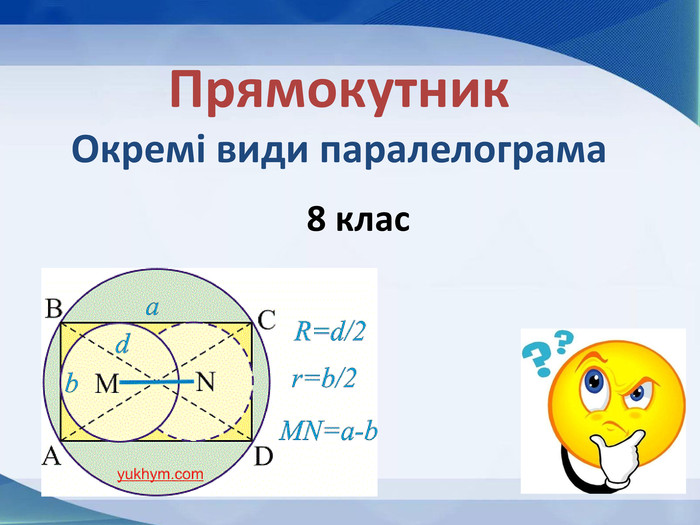
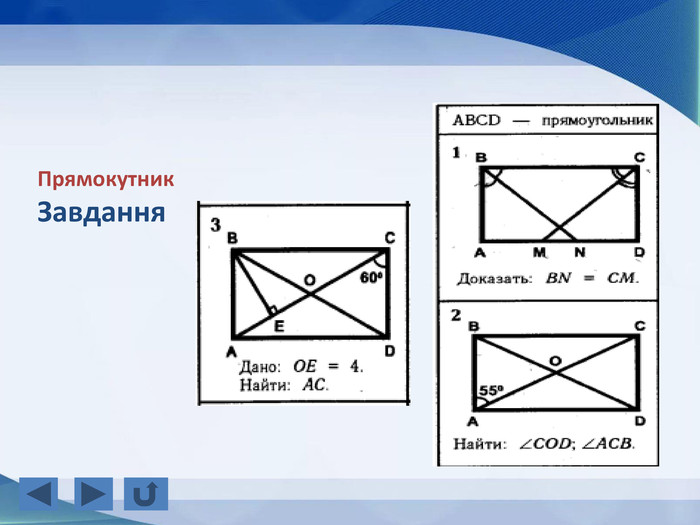
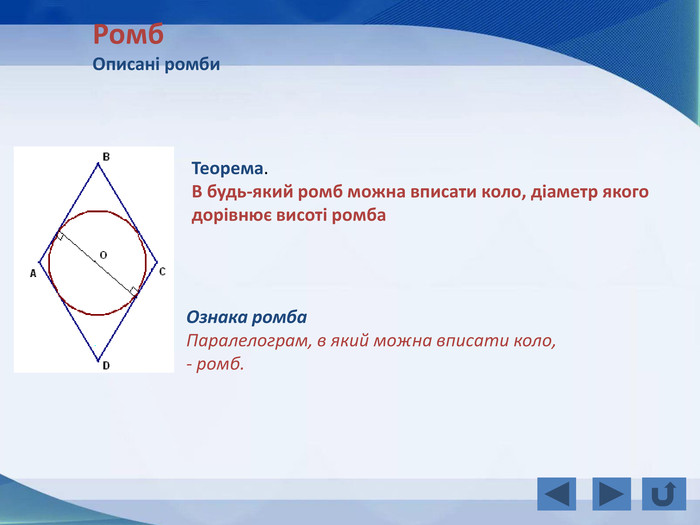
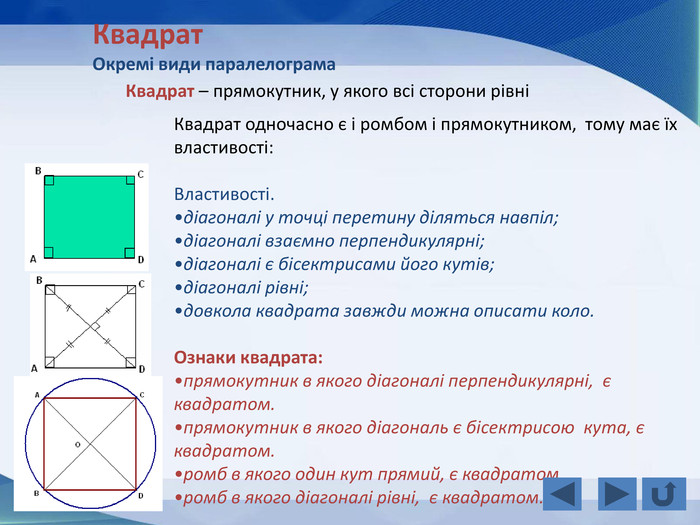
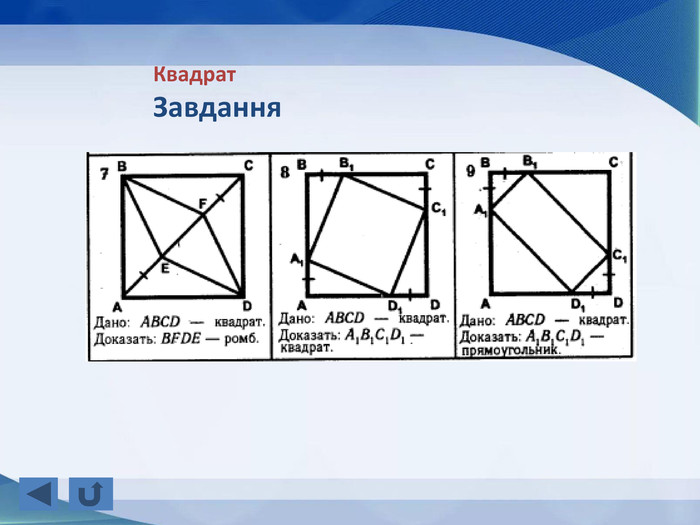
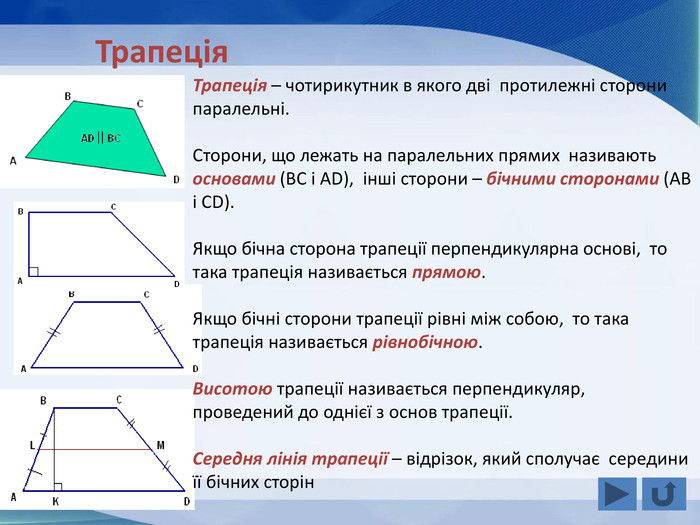
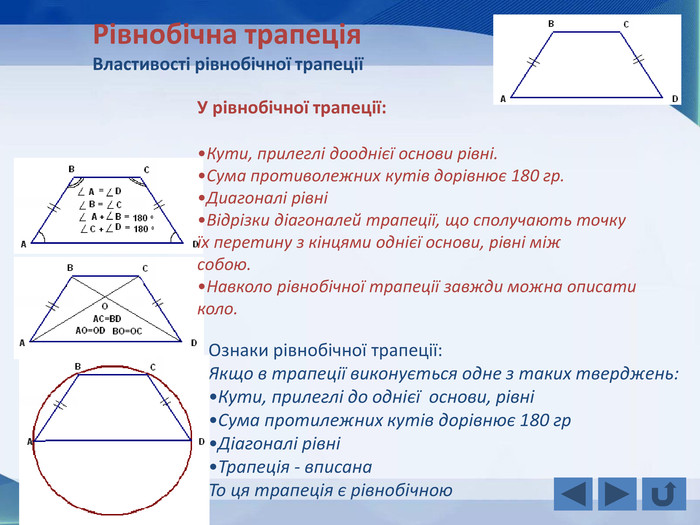
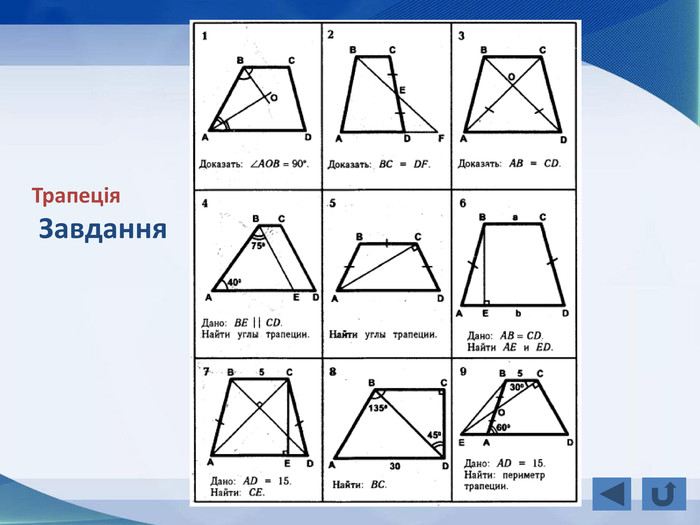
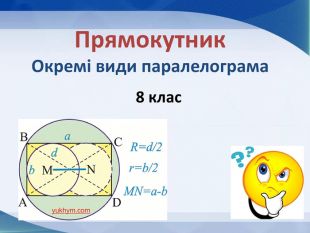
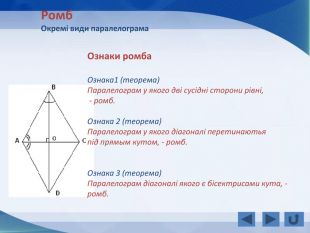
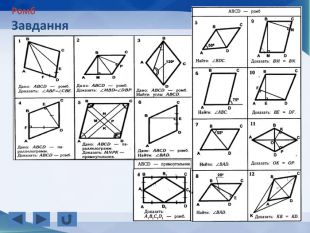
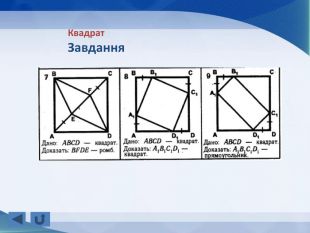
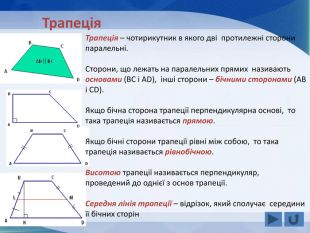
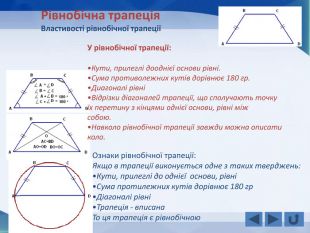
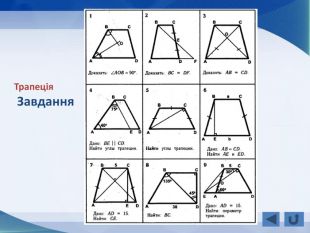
Розповідається все про тему "Прямокутник, окремі види паралелограма", а саме властивості прямокутника, ознаки прямокутника, завдання, теореми, властивості ромба, ознаки ромба, теореми, завдання, властивості квадрата, завдання, все про трацеції: властивості, рівнобічна трапеція, завдання Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку