Презентація + Робочий зошит з теми + На допомогу учневі (підбірка матеріалу)
Матеріал призначений для більш ширшого вивчення теми "Комбінаторика".
Містить презентацію. "Робочоий зошит" містить завдання для ДПА.
Без врахування впливу випадкових явищ,
людина стає безсилою спрямовувати
розвиток процесів, які її цікавлять,
в потрібному їй напрямку
Б. В. ГНЕДЕНКО
КОМБІНАТОРИКА
РОБОЧИЙ ЗОШИТ
Уч.________ гр._________________ КВПУ
________________________________________
призвіще та ім’я
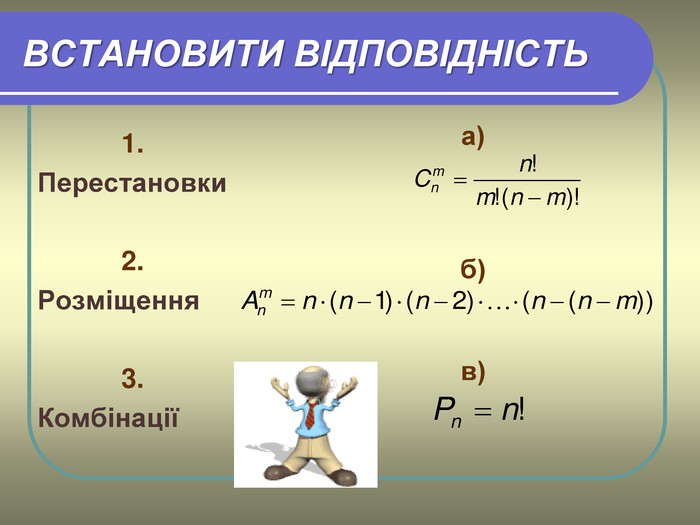
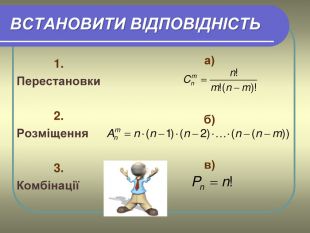
1.Встановити відповідність:
1. а)
Перестановки ![]()
2. б)
Розміщення ![]()
3. в)
Комбінації ![]()
2.Обчислити (усно):
а) ![]() ; б)8! – 6!; в)
; б)8! – 6!; в) ![]() ; г)
; г)![]() .
.
3.Задача. У класі 18 учнів. Скількома способами можна обрати 23 чергових?
а) знайти помилку в умові задачі;
б) заповнити прогалини в розв’язанні.
Розв’язання. Оскільки 23 чергових з 18 учнів обрати ……………………. ,то вважатимемо, що необхідно обрати …… чергових. Обирання .......... з 18 учнів є одним із варіантів кількості комбінацій ![]() або
або ![]() .
.
![]() ...
...
![]() або
або ![]()
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:_______________________________
4.Задачі з збірника завдань для ДПА:
а) варіант - із записом розв’язку на дошкі.
б) варіант - колективна робота,
в) варіант -з коментуванням,
Розв’язання._________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:___________________________________________
5. За формулою бінома Ньютона записати розклад степеня ( і знайти 6-й член розкладу):
а) (x2+2y2)4 б) (a – 2b)8.
Розв’язання. а)______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
б)______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________
6. Задача. Молодий український дизайнер працює над створенням нової моделі одягу. Скільки варіантів він має при виборі кольорової гами костюма, якщо костюм може бути робочим, вечірнім, сценічним чи іншим? Вважати, що основними є кольори веселки.
- Узагальніть розв’язок задачі для n кольорів.
- Змініть умову задачі для інших даних: а) 7 днів у тижні; б) 7 уроків.
Розв’язання: ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:_________________________________________________________________________
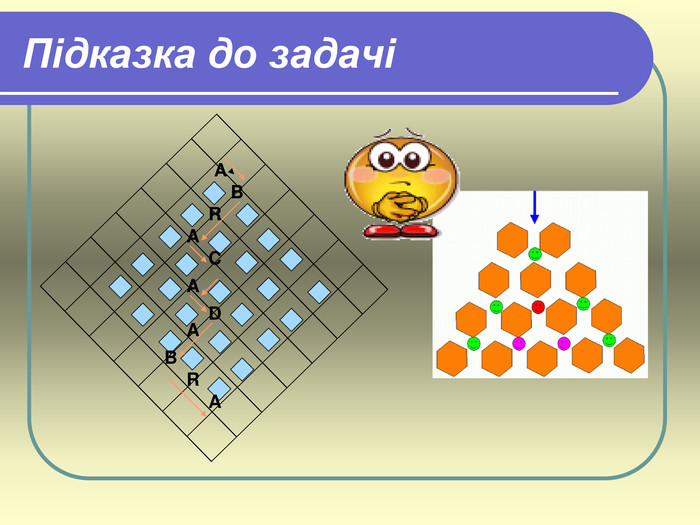
7. Задача. Скількома способами можна прочитати слово «АБРАКАДАБРА» ?
А
В В
R R R
A A A A
C C C C C
A A A A A A
D D D D D
A A A A
B B B
R R
A
Розв’язання._________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________

1
Зміст
- Вступ__________________________________________2
- Перестановки___________________________________3
- Факторіал______________________________________ 3
- Розміщення_____________________________________4
- Комбінації______________________________________4
- Біном Ньютона__________________________________5
- Біноміальні коефіцієнти__________________________5
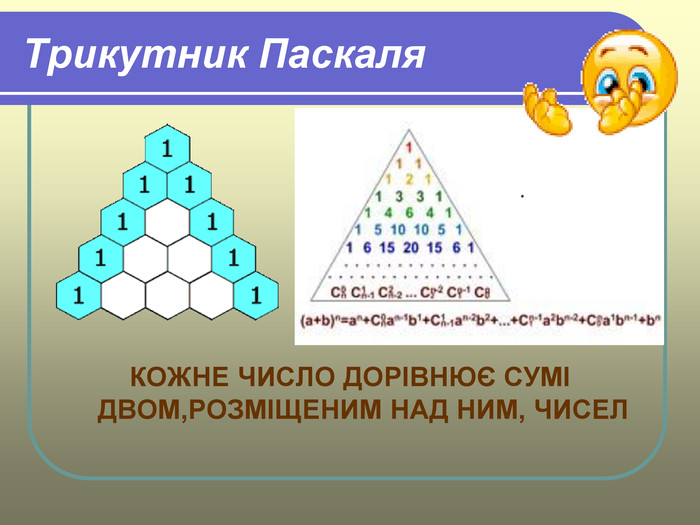
- Трикутник Паскаля______________________________6
- Властивості біноміальних коефіцієнтів_____________6
10. Тренувальні вправи____________________________9
Вступ
Представникам різних професій доводиться розв’язувати задачі, в яких з деякої множини об’єктів потрібно вибирати елементи, що мають ті або інші властивості, розміщувати ці елементи в певному порядку. Так керівнику цеху потрібно розподілити кілька видів робіт між працівниками, агроному – розмістити посіви сільськогосподарських культур на кількох полях, хіміку – розглянути можливі зв’язки між атомами і молекулами, тощо. Оскільки в таких задачах йде мова про комбінування об’єктів, їх називають комбінаторними задачами, а розділ математики, в якому вивчаються питання про те, скільки різних комбінацій, що відповідають тим чи іншим умовам можна скласти із заданих об’єктів, називають комбінаторикою.
В наш час комбінаторні задачі приходиться розв’язувати фізикам, хімікам, біологам, економістам, спеціалістам самих різних професій.
Перестановки
Візьмемо n різних елементів : а1, а2, а3, … аn. Будемо переставляти їх усіма можливими способами, зберігаючи їхню кількість і змінюючи лише порядок їх розташування. Кожна із отриманих таким чином комбінацій називається перестановкою. Загальна кількість перестановок із n елементів позначається Рn. Це число дорівнює добутку всіх цих чисел від 1 до n :
![]()
Символ n! - називається факторіалом, - є скороченим записом добуту : ![]() .
.
Нижче наведено значення факторіала для значень n від 1 до 10.
1!=1
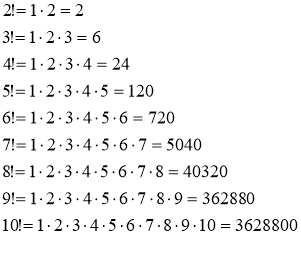
Задача. Знайти число перестановок з трьох елементів: а, в ,с.
Розв’язання.
Згідно наведеній формулі : Р3=1 2 3=6, дійсно ми маємо 6 перестановок : авс, асв. вас, вса, сав, сва.
Розміщення
Будемо складати групи із m різних елементів, взятих із множини, що складається із n елементів в різноманітному порядку. Отримані комбінації називаються розміщеннями із n елементів по m .
Кількість розміщень з n елементів по m позначають символом ![]() і дорівнює добутку:
і дорівнює добутку:
![]() .
.
Тобто число розміщень з n елементів по m дорівнює добутку m послідовних натуральних чисел, найбільше з яких m .
Якщо n= m, то маємо ![]() =Рn, тобто перестановка – окремий випадок розміщення.
=Рn, тобто перестановка – окремий випадок розміщення.
Задача. Знайти число розміщень із чотирьох елементів : a, b, c, d по два.
Розв’язання.
Згідно формули ![]() .
.
Отже, маємо такі розміщення : ab, ba, ac, ca, ad, da, dc, cd, bc, cb, bd, db.
Комбінації
Будемо складати групи із m різних елементів, взятих із множини, що складається із n елементів, не приймаючи до уваги порядок розміщення цих m елементів.
В цьому випадку ми отримаємо комбінацію з n елементів по m.
Число комбінацій з n елементів по m позначають символом ![]() і може бути обчислено по формулі :
і може бути обчислено по формулі :
 або
або 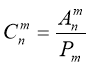
Відмітимо, що можна скласти тільки одну комбінацію із n елементів по n яка містить всі n елементів. Формула кількості комбінацій дає таке значення лише за умови, якщо вважати, що 0!=1, що є означенням 0!
Згідно цього означення :
![]() ,
, ![]()
Задача. Знайти число комбінацій з п’яти елементів : a, b, c, d, e по три .
Розв’язання
![]() .
.
Маємо десять комбінацій : abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.
Біном Ньютона
Біном Ньютона – це алгебраїчна формула, відкрита Ньютоном, яка дає змогу подати двочлен (біном) в будь – якому степені, а саме : ![]()
Зауважимо, що сума показників степеня а і в постійна і рівна n.
Задача. Піднесіть до шостого степеня 1+х.
Розв’язання.
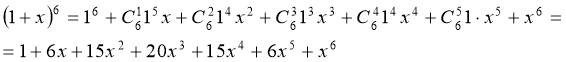
Властивості формули бінома Ньютона
- В правій частині формули міститься (n +1) членів, оскільки розклад включає всі степені b від 0 до n.
- Позначимо k член розкладу через Tk
T1=Cn0anb0=an, T2=Cn1an-1b=nan-1b,
Tk=Cnk-1an-k+1bk-1, Tk+1=Cnkan-kbk
- Показник а послідовно зменшується на 1, а показник b- збільшується на 1.Внаслідок цього сума показників степенів а і b в кожному члені стала і дорівнює показнику степеня бінома n.
- Коефіцієнти членів, рівновіддалених від початку і кінця розкладу, рівні між собою.
- Сума біномінальних коефіцієнтів дорівнює 2n.
- Щоб дістати біноміальний коефіцієнт наступного члена, слід біноміальний коефіцієнт попереднього помножити на показник степеня а в цьому члені і розділити на число попередніх членів.
Оскільки ![]() , то
, то ![]()
Дана формула дає змогу обчислювати будь-який член натурального степеня бінома.
Наприклад. Знайти восьмий член розкладу(x-a)12.
Розв’язання.
(x-a)12=(x+(-a))12.
За формулою загального члена розкладу бінома маємо:
T8 = T7+1 = C127x12-7(-a)7 = -C127x5a7 = -C127x5a7 = -1584a7x5.
Біноміальні коефіцієнти
Числа ![]() називаються біноміальними коефіцієнтами.
називаються біноміальними коефіцієнтами.
Їх можна обчислити, застосувавши тільки додавання, якщо користуватись при цьому наступною схемою. В верхньому рядку пишемо дві одиниці. Всі наступні рядки починаються і закінчуються одиницею. Проміжні числа в цих рядках одержують в результаті додавання сусідніх чисел із попереднього рядка. Така схема називається трикутником Паскаля:

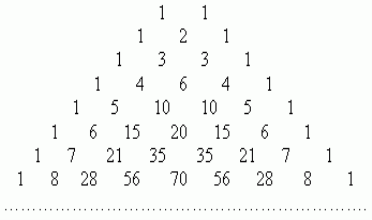
Перший рядок в цій таблиці містить біноміальні коефіцієнти для n=1, другий – для n=2, третій – для n=3 і т. д. Тому, якщо необхідно, наприклад, розкласти вираз (а + в)7 , ми можемо скористатися таблицею і швидко отримати результат:
(а + в)7=а7+7а6в+21а5в2+35а4в3+35а3в4+21а2в5+7ав6+в7.
Властивості біномінальних коефіцієнтів:
1.Сума коефіцієнтів розкладу (а + в)n дорівнює 2 n.
2.Коефіцієнти членів, рівновіддалених від кінців розкладу, рівні.
3.Сума коефіцієнтів парних членів розкладу дорівнює сумі коефіцієнтів непарних членів розкладу; кожна з них дорівнює 2 n-1
(а+в)0 = 1 1
(а+в)1 = а+в 1 1
(а+в)2 = а2+2ав+в2 1 2 1
(а+в)3 = а3+3а2в+3ав2+а3 1 3 3 1
(а+в)4 = а4+4а3в+6а2в2+4ав3+в4 1 4 6 4 1
(а+в)5 = … 1 5 10 10 5 1
(а+в)6 = … 1 6 15 20 15 6 1
Т Р Е Н У В А Л Ь Н І В П Р А В И
ПЕРЕСТАНОВКИ
1.Обчислити:
а)![]() ; г)
; г) ![]() ; є)
; є) ![]() ;
;
б)![]() ;
;
в)5! – 4!; д) ![]() ; ж)
; ж)![]() .
.
2.Скільки чотирицифрових чисел можна утворити з цифр 0,1,2,3 не повторюючи їх?
3.В групі 35 студентів. Вони обмінялись один з одним фотокартками. Скільки всього фотокарток було роздано?
4.Скільки різних прямих можна провести через 10 точок площини, з яких жодні три не лежать на одній прямій?
5.Скільки різних слів можна одержати, переставляючи букви слова «училище».
6.Спростити:
а)![]() ; б)
; б)![]() ; в)
; в)![]() .
.
КОМБІНАЦІЇ
1.Обчислити:
а)![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г) ![]() .
.
2.Довести, що:
а)![]() ; б)
; б)![]() .
.
3.Спростити вираз:
а)![]() ; б) )
; б) )![]() .
.
4.Обчислити:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
5.Довести, що:
а) ![]() ;
;
б)![]() .
.
6*.Шістнадцять екскурсантів розділилися на дві рівні групи для розшуку товариша, який заблукав. Серед них є лише 4, хто знає місцевість. Скількома способами вони можуть розділитись так, щоб до кожної групи ввійшли дві особи, які знають місцевість?
7.У групі 32 студенти. Скількома способами можна сформувати команду з 4 чоловік для участі у конкурсі професійної майстерності?
8. Скількома способами можна бригаду з 17 робітників, можна розділити на дві групи так, щоб у одній групі було 5 чоловік, а у другій – 12 чоловік?
9.На одній паралельній прямій позначено 7 точок, на другій – 12. Скільки існує чотирикутників з вершинами в цих точках?
Р О З М І Щ Е Н Н Я
1.Знайти значення виразу:
а)![]() ; б)
; б) ![]() .
.
2.Розвязати рівняння:
а)![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Скільки існує правильних дробів, чисельник і знаменник яких прості числа, не більші за 20?
БІНОМ НЬЮТОНА
1.Обчислити: а) 295=(30 -1)5=… б) 995=(100 – 1)5.
2.За формулою бінома Ньютона знайти розклад степеня:
а) (а + в)5; е) (а + 2b)5 ;
б) (m + n)7; є) (x2- 2y2 )4;
в) (x – y)4; ж)(3x – 1)4;
г)(![]() )4; з)(а2 – 1)5.
)4; з)(а2 – 1)5.
д) (3x+4y)6 ; к) (x- ![]() )5.
)5.
3,Знайти шостий член в розкладі бінома 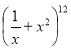 .
.
4.Знайти четвертий член в розкладі бінома ![]() .
.
5.В розкладі бінома 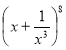 знайти номер члена, який не містить x.
знайти номер члена, який не містить x.
-
В розкладі бінома
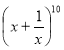 знайти номер члена, який не містить x.
знайти номер члена, який не містить x.
З А В Д А Н Н Я З З Б І Р Н И К А Д Л Я ДПА
В2.1.7.Скільки чотирицифрових чисел з різними цифрами можна записати, використовуючи цифри 0, 1, 2, 3?
А) 24; Б) 18; В) 20; Г) 16
В5.1.10.З 4 студентів потрібно вибрати двох для поїздки за кордон. Скільки варіантів вибору цих двох студентів існує?
А) 6; Б) 12; В) 15; Г) 18.
В9.1.12.Скількома способами можна сформувати комісію з 3 осіб, яких треба вибрати з 4 претендентів.
А) 3; Б) 4; В) 6; Г) 12.
В11.1.11.Скільки існує звичайних дробів, чисельник і знаменник яких - різні прості числа, не більші за 20?
А) 14; Б) 28; В) 56; Г)70.
В13.1.12Скільки трицифрових чисел з різними цифрами можна записати, використовуючи цифри 1,2,3,4,5,6?
А)120; Б)720; В)20; Г) 216.
В15.1.11.У меню їдальні є 3 перші страви, 6 других страв і 4 треті страви. Скількома способами можна вибрати обід, який містить по одній страві кожного виду?
А) 13; Б)36; В)72; Г)54.
В17.1.12.На площині позначено 10 точок так, що жодні три з них не лежать на одній прямій. Скільки існує трикутників з вершинами у цих точках?
А) 120; Б) 720; В) 240; Г) 360.
В18.1.11.Оркестру потрібні скрипаль, піаніст і флейтист. На місце скрипаля є 7 кандидатів, на місце піаніста – 5, а на місце флейтиста – 2. Скільки існує варіантів нового складу оркестру?
А) 14; Б) 35; В) 50; Г) 70.
В19.1.11.Скільки існує трицифрових чисел, усі цифри яких непарні і різні?
А) 30; Б) 60; В)120; Г) 150.
В21.10.З десяти учнів потрібно вибрати двох для прибирання класної кімнати.
Скількома способами це можна зробити?
А) 120; Б) 90; В) 60; Г) 45.
В23.1.11.Скілько двоцифрових чисел з різними цифрами можна записати, використовуючи цифри 1; 2; 3?
А) 4; Б)5; В) 6; Г)8.
В24.1.12. Розклад одного дня містить 4 уроки з різних предметів. Скількома способами можна скласти цей розклад, маючи вибір з 10 предметів?
А) 210; Б) 40; В) 1280; Г) 5040.
В27.1.12.Скількома способами можна вибрати 2 кульки і 2 кубики з 6 різних кульок і 5 різних кубиків?
А) 75; Б) 150; В) 480; Г) 120.
В29.1.11.Скількома способами можна розставити на полиці 5 різних книжок?
А) 60; Б) 120; В) 25; Г) 240.
В35.1.11.У магазині є 7 видів новорічних подарунків. Скількома способами можна вибрати з них три різні подарунки?
А)35; Б) 70; В) 140; Г) 210.
В36.1.12Скільки чотирицифрових чисел, кратних 5, усі цифри яких різні, можна записати, використовуючи лише цифри 1, 2, 3, 4, і 5?
А) 16; Б)24; В)28; Г)32.
В40.1.12.У футбольній команді, яка складається з 11 гравців, потрібно вибрати капітана та його заступника. Скількома способами це можна зробити?
А) 22; Б) 220; В) 55; Г) 110.
В45.1.12.Розглядаються п’ятицифрові числа, у запису яких двічі присутня цифра 3 і по одному разу кожна з цифр 1,2 і 4. Скільки існує таких чисел?
А) 60; Б) 80; В) 120; Г) 150.
В48.1.12.Скільки парних п’ятицифрових чисел, усі цифри яких різні, можна записати, використовуючи цифри 3,4,5,7, і 9?
А) 24; Б) 12; В) 120; Г) 60.
В52.1.7.Скільки п’ятицифрових чисел з різними цифрами можна записати, використовуючи цифри 6,7,8,9,0?
А) 120; Б) 100; В) 108; Г) 96.
В55.1.10.З 4 учнів потрібно вибрати трьох для виступу в святковому концерті. Скільки варіантів вибору цих трьох учнів існує?
А)16; Б)12; В)8; Г)4.
В57.1.12.У конкурсі ерудитів взяло участь 10 учнів. Скільки є варіантів розподілу перших трьох місць?
А) 600; Б) 720; В) 820; Г) 1000.
В59.1.12.Убригаді робітників з 8 осіб треба сформувати групу з 3 осіб, які мають їхати у відрядження. Скількома способами це можна зробити?
А) 56; Б) 48; В) 36; Г) 28.
В61.1.11.Скільки існує на координатній площині точок, абсциса і ордината яких – різні складені числа, не більші за 18?
А) 90; Б) 72; В) 54; Г) 36.
В63.1.12.Скільки двоцифрових чисел з різними цифрами можна записати, використовуючи цифри 1,2,3,4,5,6?
А) 60; Б) 30; В) 48; Г) 36.
В67.1.12.На площині позначено 10 точок так, що жодні три з них не лежать на одній прямій. Скільки існує прямих, що проходять через ці точки?
А) 45; Б) 90; В) 60; Г) 120.
В68.1.11.Маємо 8 різних конвертів і 4 різних марки. Скількома способами можна вибрати конверт і марку?
А) 12; Б) 16; В) 32; Г) 64.
В69.1.11.Скільки існує трицифрових чисел, усі цифри яких різні, парні і відмінні від нуля?
А) 12; Б) 24; В) 36; Г) 40.
В71.1.10.З 12 робітників треба сформувати ремонтну бригаду з 3 осіб. Скількома способами це можна зробити?
А) 132; Б) 110; В) 220; Г) 440.
В73.1.11.Скільки двоцифрових чисел з різними цифрами можна записати, використовуючи цифри 1; 2; 3 і 4?
А) 6; Б) 8; В) 12; Г) 18.
В74.1.12.З 12 спортсменів треба вибрати чотирьох для участі в легкоатлетичній естафеті і розставити їх по етапах естафети. Скількома способами можна це зробити?
А) 495; Б) 11880; В) 12800; Г) 9600.
В77.1.12.Скількома способами можна вибрати 3 олівці та 2 ручки із 5 різних олівців і 4 різних ручок?
А) 60; Б) 16; В) 80; Г) 32.
В79.1.11.Скількома способами можна доїхати з міста А через місто В у місто С, якщо з А до В веде 4 дороги, а з В до С – 6 доріг?
А) 10; Б) 12; В) 18; Г) 24.
В85.1.11.Потрібно вибрати з 10 членів учнівської ради школи голову, його заступника і секретаря ради. Скільки є різних варіантів їх вибору?
А) 720; Б) 810; В) 900; Г) 1000.
В86.1.12.Скільки чотирицифрових чисел, кратних 2, усі цифри яких різні, можна записати, використовуючи лише цифри 5,6,7,8 і 9?
А) 12; Б) 24; В) 36; Г) 48.
В90.1.12.Скількома способами у змаганнях, у яких бере участь 10 команд, можуть розподілитися три перші місця?
А) 90; Б)180; В) 360; Г) 720.
В95.1.12.Розглядаються чотирицифрові числа, у запису яких двічі присутня цифра 5 і по одному разу кожна з цифр 6 і 7. Скільки існує таких чисел?
А) 30; Б) 24; В) 18; Г) 12.
В98.1.12.Скільки шестицифрових чисел, які кратні числу 10 і всі цифри яких різні, можна записати, використовуючи цифри 0,1,2,3,4 і 5 ?
А) 36; Б) 60; В) 24; Г) 120.
В100.1.12.У шкільній їдальні є 4 види соків та 4 види пиріжків. Скількома способами учень може взяти для підвечірку склянку соку та два різні пиріжки?
А) 8; Б) 12; В) 16, Г) 24.
1


про публікацію авторської розробки
Додати розробку