Презентація "Усний журнал: «Математика і мистецтво»"

Усний журнал «Математика і мистецтво»Для учнів 9 класу. Підготовчий етап: Проект «Математика і мистецтво»Вч. Математики: Лукичова Н. С.

познайомити учнів зі світом математики та мистецтва;підвищити навички роботи з сучасними інформаційно-комунікаційними технологіями, мережею Інтернет тощо;розвивати критичне, логічне мислення; розвивати пошукові навички;підвищити інтерес до навчання, зокрема вивчення математики. Показати зв'язок та важливість вивчення математики. Виховувати культуру, почуття прекрасного. Мета

Вступна частина. Подорож чарівним світом математики і мистецтва. Зупинка «Математика та живопис»Зупинка «Математика та архітектура»Зупинка «Математика та література»Зупинка «Математика та музика»Заключна частина. План

«Математика володіє не тільки істиною, а й найвищою красою – красою відточеною і суворою, … піднесено чистою і такою, що прагне до справжньої досконалості, яка властива тільки найкращим зразкам мистецтва» Б. Рассел

Математика, якщо на неї правильно подивитися, відображає не тільки істину, але і незрівнянну красу. Велика книга природи написана математичними символами. Галілей

Більшість людей вважають, що математика займається виключно числами та вимірюваннями, однак, насправді математика – це дещо набагато більше, ніж просто наука для касирів… Математика та мистецтво: на сьогоднішній день ці дві великі сфери культури сприймаються як два полюса і навіть як дві протидіючі сили, в той час, коли насправді вони зв’язані міцними путами.

На певному етапі свого розвитку людину почало турбувати питання: «Чому той чи інший предмет являється гарним і що є основою прекрасного?» Краса скульптури, храму, картини, симфонії, поеми... Що між ними спільного? Хіба можна порівняти красу скульптури з красою музики? Виявляється, можна, якщо будуть винайдені єдині формули прекрасного, які будуть об'єднувати поняття прекрасного найрізноманітніших об'єктів – від квітки ромашки до краси музики.

Ще у епоху Відродження художники відкрили, що будь яка картина має певні точки, що мимоволі привертають нашу увагу, так звані зорові центри. Таких точок всього чотири, і розміщені вони на відстані 3/8 та 5/8 від відповідних країв площини. Це відкриття у художників того часу отримало назву «золотий переріз» картини. Зупинка «Математика та живопис»«Ні один живописець не може писати , не знаючи геометрії.» Л. Альберті

Це такий пропорційний поділ відрізка на нерівні частини, при якому довжина усього відрізка відноситься до більшої частини, як сама більша частина відноситься до меншої:a : b= b : c або с : b= b : а Золотий переріз – гармонійна пропорція.

Саме вивченню «золотого перерізу» приділяв багато своєї уваги великий італійський художник, учений Леонардо да Вінчі . Особистість Леонардо да Вінчі – одна із загадок у історії. Сам учений говорив: «Нехай ніхто, що не є математиком, не наважиться читати мої праці». Він дістав славу талановитішого художника, великого ученого, генія, що передбачив багато винаходів, які не були впроваджені майже до ХХ ст. Леонардо да Вінчі

«Живопис приходив до математики через учіння про перспективу і через оптику , скульптура – через учіння про пропорції , архітектура – через учення про масу й вагу тіл і через те ж учіння пропорції. Мистецтво ставало наукою. Ніхто не почував цього так ясно і сильно, як Леонардо да Вінчі, і недарма в його творчості мистецтво й наука стали двома сторонами одного й того самого, чимось неподільним.» О. К. Дживелегов

Леонардода ВінчіЕпоха Відродження

Леонардо да Вінчі “Мона Ліза” Монолог Мони Лізи Уже віки ви дивитесь на мене, Всі дивитесь на усмішку мою. Я ж перед вами стільки літ стою І мила, і проста, і незбагненна. Не думайте, що дуже легко це – Між поглядів захоплених , і хтивих, І ніжних, і скорботних, і вразливих Ховати тільки душу, не лице.

Альбрехт. Дюрер-німецький живописець, гравер, гуманіст, учений (1471 – 1528)

А. Дюрер “Меланхолія”

Моріс Корнеліс Ешер –нідерландський художник-графік (1898-1972)

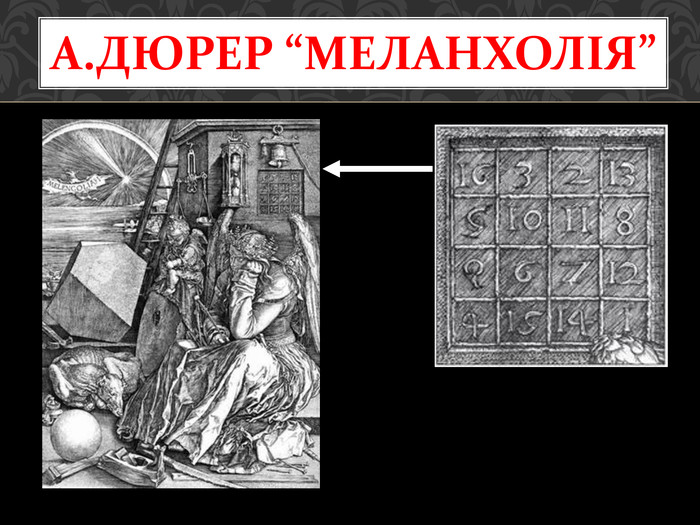
«Геометрія володіє двома скарбами: один з них - це теорема Піфагора, а інший - поділ відрізка в «золотому перерізі». Перший можна порівняти з мірою золота, другий ж більше нагадує дорогоцінний камінь » Йоганн Кеплер Пентаграма - таємний знак піфагорійського братства - була обрана ними як символ життя і здоров'я.

«Ні тридцять років ні тридцять сторіч не роблять ніякого впливу на ясність або на красу геометричних тіл» Керрол Л. (Додгсон)Раїфський чоловічий монастир - єдиний монастирський комплекс, що зберігся в Татарії, побудований в XVII столітті. Комплекс має форму п'ятикутника. Пентагон в США. Комплекс має форму правильного п'ятикутника, витканого із золотих пропорцій.

Зупинка «Математика та архітектура»«Симетрія – широка тема, яка має велике значення для мистецтва і природи. Біля джерел симетрії лежить математика: щоб показати, як працює математичне мислення, навряд чи можливо знайти щось краще, ніж симетрія.» Г. Вейль

Будь-яка архітектурна споруда використовує симетрію Йдучи вулицями міста, можна спостерігати, як геометричні форми використовуються в архітектурі. Подивимось на найвідоміші архітектурні пам’ятки світу: … Ми бачимо колони, арки, ніші, фризи, ажурні бароківські ліплення складної форми. Лише досконале знання архітектором математики дає можливість поєднати здавалося б прості геометричні форми (куб, паралелепіпед, циліндр, еліпс, коло) у складну музику вишуканих будівель. Результат роботи архітектора повинен бути точним. Його перспективний малюнок повинен відповідати правилам геометрії, зокрема нарисної. Отже , ні один архітектор не обійдеться без знання масштабу, пропорції, симетрії.

Математика і архітектура. З усіх видів мистецтва архітектура, мабуть, ближче з усіх до математики: тому що, за основу конструкцій покладені найточніші розрахунки. У давнину, окрім відомих нині дев'яти муз, існувала і муза математики, тобто математика вважалася мистецтвом рівним астрономії, муза якої входить в склад свити Аполлона – ватажка усіх муз. Так і уявляєш собі, що по один бік Математики стоїть Архітектура, а по інший – Музика, яка також не може існувати без ритму, без рахунку, без яких в свою чергу немає гармонії.

«Для людського розуму симетрія має, мабуть, цілком особливу приваблюючу силу. Нам подобається дивитись на прояв симетрії в природі, на ідеально симетричні кристали, на сніжинки, нарешті, на квіти, які майже симетричні.» Р. Фейнман

Найпрочнішою архітектурною спорудою з давніх часів вважаються єгипетські піраміди. «Раціональність» геометричної форми піраміди, що дозволяє обрати і великі розміри для цієї споруди, придає піраміді велич та красу.

Зупинка «Математика та література»«Математика і поезія це… вираження тієї самої сили уяви, тільки в першому разі уява звернена до голови, а в другому – до серця.» Т. Хілл

Люди вирішили, що мистецтво та наука - явища дуже різні, щоб ними займалася одна людина. Але вчений та художник в одній особі – це не суперечність, а, навпаки, гармонія. Коротенькі вірші О. Хайяма – рубаї – поєднання математичної точності та сердечного трепету. Рубаи Омара Хайяма: О тайнах сокровенных невеждам не кричи,И бисер знаний ценных перед глупым не мечи,Будь скуп в речах и прежде взгляни, с кем говоришь,Лелей свои надежды, но прячь от них ключи. То, что судьба тебе решила дать,Нельзя ни увеличить, ни отнять. Заботься не о том, чем не владеешь,А от того, что есть, свободным стать.

Омар Хайям. Видатна особистість Сходу ХІ століття

Софія Ковалевська(1850 – 1891) «Математика – наука , яка вимагає найбільше фантазії … не можна бути математиком, не будучи водночас і поетом у душі.»

М.І. Лобачевський(1792 – 1856) Завоював почесне звання “Коперник геометрії”

Рене Декарт1596-1650філософ, математик, фізик, фізіолог

Володимир. Андрійович. Стеклов1864-1926

М. В. Остроградський(1801 – 1862)

Ейлерматематик,фізик, механік,астроном1707-1783

Льюіс Керрол(1832 – 1898)

Льюіс Керролл (справжнє імя – Чарльз Латуідж Доджсон). Наукові роботи Керролла передбачили деякі ідеї математичної логіки. Але більше він відомий як автор популярних повістей для дітей. Так в 1865 році він видав казку «Аліса в країні чудес». Королева Англії, прочитавши книгу, прийшла у захват від казки і наказала терміново придбати інші твори Керролла. І дуже здивувалася, коли з'ясувалося, що всі інші твори Керролла - твори з вищої математики, порівняльної анатомії, палеонтології і систематики тварин.

Ніхто не помічав, що в самій назві романа Льва Миколайовича Толстого – «Війна і мир» - закодований закон золотого переізу. Насправді, назва роману побудовано на перших чотирьох членах ряду Фібоначчі 1, 2, 3, 5. Один прийменник, два іменника, три слова. П'ять букв в першому ключевому слові. Відношення ключових слів 5:3=1,666… тобто перше раціональне наближення коефіціента золотого перерізу.

Літературним творам теж притаманні математичні закони: окремі сюжети письменники навіть будують з урахуванням певних математичних закономірностей або теорем. Так виникають нові оригінальні літературні твори. Одним з прикладів такого використання математичних закономірностей є видатна трагедія Гете «Фауст».

Математика вища є найвища музика, найвище мистецтво, це гармонія загальних ідей і інтуїції. М. В. Бугаєв. Зупинка «Математика та музика»Музика - найбільш суб'єктивна з наук, і найбільш абстрактно логічне з мистецтв. Бо музика - то є Гармонія Душі.

музика – математика почуття. Математика – музика розуму,

«Чи не може музика бути описаною як математика почуттів, а математика як музика розуму ? Так, наприклад, музикант відчуває музику, математик розуміє музику, - музика це мрія, математика - ділове життя – кожна повинна дістати своє завершення від другої, коли людський розум, піднесений до досконалого зразка, сяятиме далі, уславлений у якомусь майбутньому Моцар том – Діріхле чи Бетховеном – Гауссом – такий союз виразно виявляється в генії і працях Гельмгольца!» Дж. Сильвестр. Сільвестр Джеймсанглійський математик1814-1897

Коливання і струни і вивчали піфагорійці. Вони використовували для цього нескладний прилад під назвою монохорд, що являє собою єдину струну, закріплену у двох точках над резонатором.

Монохорд

А. Енштейн писав: “Ми відкрили щось подібне на коливання струни і атому, що випромінює промені, така система частин веде себе подібно до малого акустичного інструменту, в якому виробляють стоячі хвилі”. Музика є радість душі, яка обчислює, сама того не усвідомлюючи. Г. Лейбніц

Лейбніц Готфрід Вільгельм1646 - 1716 Музика є радість душі, яка обчислює, сама того не усвідомлюючи.

“Математика вища є найвища музика, найвище мистецтво, це гармонія загальних ідей і інтуїції” М. В. Бугаєв. Бетховен за роботоюсимфонія № 5

«Винайдений Моцартом спосіб компонувати мелодію за допомогою гри в кості над спеціальною таблицею, яка визначає вибір наступного такту створюваної п’єси, свідчить про те, що великі композитори чітко усвідомлювали роль випадковості в загальній побудові музичного повідомлення» А. Моль. Вольфганг Амадей Моцарт

Великий німецький композитор XVII століття Іоганн Себастьян Бах писав церковну музику. Пізніше вже після його смерті музиканти-дослідники з'ясували, що багато мелодій композитора мають цифрові коди - символи, а твори точно математично прораховані

Ігор Стравінський, який добре знав музику майстрів епохи Ренесансу, також знаходив багато спільного між математикою і музикою. «Спосіб композиторського мислення - спосіб, яким я мислю, - мені здається, не дуже відрізняється від математичного», «музична форма математична хоча б тому, що вона ідеальна» - ці вислови Стравінського яскраво виражають його переконання

Дякую за увагу!https://drive.google.com/open?id=1lro. Tq. XBgj. Z6x. PULr. Z2 C_hv. E6dml24i6s. Можете переглянути відео, перейшовшиза посиланням

Джерела інформації:http://svitppt.com.ua/rizne/matematika-i-mistectvo.htmlhttp://svitppt.com.ua/matematika/matematika-i-mistectvo4.htmlhttp://svitppt.com.ua/matematika/svyato-matematika-ta-mistectvo.htmlhttps://www.google.com/.... Музика : zv.fm