Презентація "Використання історизмів у шкільному курсі математики"

Використання історизмів у шкільному курсі математики Вчитель математики КОЗО “Новопокровський ЗЗСО” Трошина В. В.

ПЛАН - З історії проблеми - Елементи історії у викладанні математики в сучасних умовах - Історичні відомості та методика їх використання на уроках математики - Історичні задачі в шкільному курсі математики - Використання історичних відомостей у позакласній роботі

І.З історії проблеми “Було б злочином для людей, вивчаючи матеріали, не шанувати не тільки імен дослідників, але й їх методів і результатів, яких вони досягли.” ( М. Острогдадський, А. Блум)

Про велике освітнє та виховне значення елементів історизму у викладанні математики говорили відомі методисти: Г. Бевз, М. Бєскін, М. Бурда, В. Брадіс, Г. Глейзер, С. Ляпін, К. Малигін, О. Маркушевич, В. Молодший, М. Шевченко, І. Чистяков, В. Мрочек, Ф. Філіппович та ін.. М. Бєскін В. Брадіс О. Маркушевич

Відомості з історії математики включили в шкільні підручники та навчальні посібники автори: Г.Апостолова, Г.Бевз, М. Бурда, З. Слєпкань, М. Шкіль, В. Коваленко, В. Кривошеєв, А. Колмогоров, В. Клопський, В. Тадеєв, М. Ягодовський, М. Янченко та ін..

Впровадження історичного матеріалу у процес навчання математики є важливою умовою забезпечення гуманізації змісту математичної освіти, ефективності навчально-виховного процесу і розвитку підростаючого покоління. Муза геометрії

Багато спеціалістів вважають, що шкільний підручник не повинен містити нічого зайвого, тобто нічого, крім означень, їх ілюстрацій і пояснень, аксіом, теорем та їх доведень, прикладів і вправ для самостійного розв’язування їх учнями. Саме тому у “Підручнику з елементарної геометрії” М. Остроградського майже немає ніяких історичних довідок за винятком кількох коротких виносок, подібних до такої: “Декарт – відомий французький геометр та філософ. Народився в 1596, помер 1650 року.” У підручнику геометрії А. Кисельова розглядаються тільки питання, пов’язані з історією п’ятого постулату.

Проблема ознайомлення учнів з історією математики цікавила і нашого видатного методиста-математика О. Астряба:

ІІ.Елементи історії у викладанні математики в сучасних умовах Роль математики в різні часи оцінювали по-різному. Одні вчені розглядали її як інструмент для інженерів та науковців, інші - як засіб для розвитку логічного мислення. Тепер бажано дивитись на неї ширше: історія математики є частиною культури. Вона знайомить учнів з фактами культурного життя людства, демонструє тернистий шлях вчених та їх теорій до повного визнання і сприйняття сучасниками, можливо, лише майбутніми поколіннями. Математичні поняття, відношення і теорії завдяки історичній динамічності стають ближчими та зрозумілішими учням.

Засобами оновлення курсу шкільної математики.її гуманізації можуть стати: Дотримання методологічного філософського принципу єдності історичного і логічного Використання матеріалів з історії розвитку математики Висвітлення здобутків вітчизняних математиків Формуванння в учнів погляду на математику як на складову загальнолюдської культури

Значення історії математики у вивченні математики у школі: Освітнє – допомагає з’ясувати роль і місце математики в практичній діяльності людини; Виховне – збуджує інтерес та любов до предмету, потяг до наукової творчості, критичне ставлення до нових фактів; Розвиваюче – є ключем для розуміння логіки побудови наукових теорій.

Знайомство учнів з історією математики означає продумане, сплановане використання на уроках фактів з історії науки та їх органічне переплетення з систематичним викладом усього матеріалу програми.

- Історичні відступи на уроках, бесіда від 2-3 до 8-10 хв.; -Повідомлення історичних відомостей, органічно поєднаних з теорією чи задачами; -Спеціальні уроки з їсторії математики; -Математичні гуртки (можна організувати спеціальний історико-математичний гурток); -Історики-математичні вечори; -Організація спеціальної математично-історичної газети; -Домашні твори та реферати учнів; -Збирання елементів “народної математики”; -Бесіди, лекції, доповіді вчителя або запрошених наукових працівників. Форми введення історії у навчання математики:

ІІІ. Історичні відомості та методика їх використання на уроках математики Використання історичного матеріалу “гуманізує” і “гуманітаризує” шкільну математику. Думка, що історичний матеріал забирає багаточасу і перевантажує учнів, є хибною.Відомості з історії математики пожвавлюють уроки, дають можливістьбільш грунтовно і свідомо засвоїти математичні поняття, створюють уявлення про математику як науку, що постійно розвивається.

Виклад історичних відомостей не може бути відірваним від самої математики. Історичні екскурси можна пропонувати учням на різних етапах уроку та з різною метою:

Перед вивченням нової теми – з метою мотивації або підвищення інтересу до її вивчення Приклад: В курсі алгебри 8-го класу вивчається тема “Теорема вієта”.Як зацікавити учнів? Можна розповісти цікавий момент з життя Франсуа Вієта. За освітою він юрист і служив при дворі французького короля Генріха IV. Під час війни Франції з Іспанією Вієта знайшов ключ до шифру, який застосовували іспанці і засіб стежити за всіма змінами у ньому. Довгий час хід війни змінювався на користь Франції. Коли в Іспанії дізналися, що Вієта розшифрував їхню секретну інформацію, його заочно приговорили до спалення. Врятувало Вієта тільки те, що король не видав його іспанській інквізиції. Учням корисно буде дізнатися, що в математику Вієта увійшов шляхом самоосвіти і став “батьком символічної алгебри”. Саме у працях Вієта – алгебра стає наукою про алгебраїчні рівняння, яка грунтується на символічних позначеннях. Вієта уперше став позначати буквами не тільки невідомі, а й коефіцієнти рівнянь , що дало змогу вивчати загальні властивості рівнянь та їх коренів.

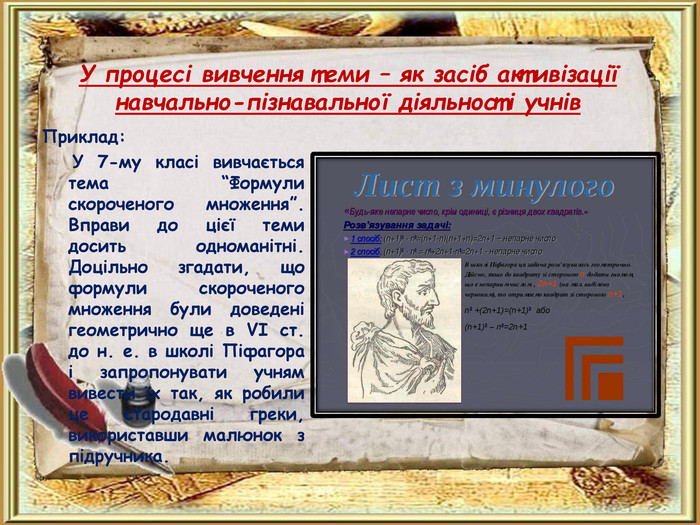
У процесі вивчення теми – як засіб активізації навчально-пізнавальної діяльності учнів Приклад: У 7-му класі вивчається тема “Формули скороченого множення”. Вправи до цієї теми досить одноманітні. Доцільно згадати, що формули скороченого множення були доведені геометрично ще в VI cт. до н. е. в школі Піфагора і запропонувати учням вивести їх так, як робили це стародавні греки, використавши малюнок з підручника.

Після вивчення і закріплення теми – з метою узагальнення та систематизації вивченого матеріалу Приклад: На уроці систематизації та корекції знань з теми “Функція” у 10-му класі бажано розглянуто еволюцію цього математичного поняття.Походить цей термін від латинського functio -діяльність, виконання. До математичного поняття “функція” найближче підійшов Р. Декарт (1637 р.). Він, як і інші математики xvii ст., кожну функцію уявляв у вигляді деякої лінії: ордината точки на даній лінії є “функція” її абсциси. Перше означення функції сформулював Й. Бернулі(1718р., фото). Л. Ейлер у кінці твору “Вступ до аналізу (1748р.) уточнив: функція змінної кількості є аналітичний вираз, складений з цієї змінної кількості і чисел або сталих кількостей.Отже, до другої половини xviii ст. поняття “функція” пов’язувалося або з геометричним її зображенням, або з аналітичним.

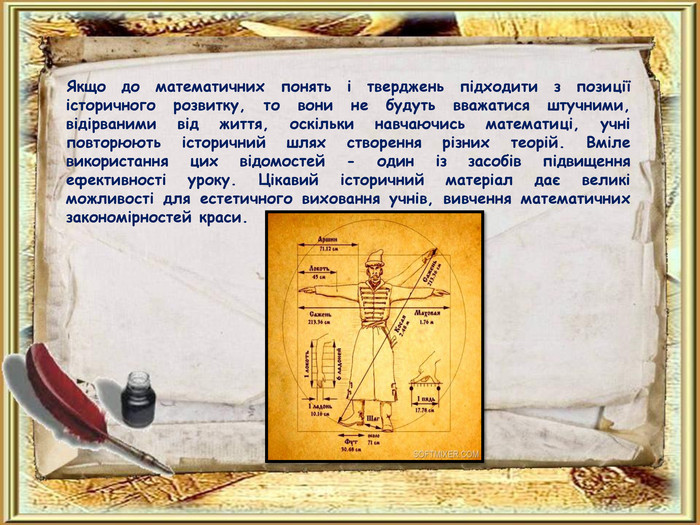
Якщо до математичних понять і тверджень підходити з позиції історичного розвитку, то вони не будуть вважатися штучними, відірваними від життя, оскільки навчаючись математиці, учні повторюють історичний шлях створення різних теорій. Вміле використання цих відомостей - один із засобів підвищення ефективності уроку. Цікавий історичний матеріал дає великі можливості для естетичного виховання учнів, вивчення математичних закономірностей краси.

Відомі математики світу Евклід (365-300 до. н. е.) Про Евкліда майже нічого невідомо, звідки він був родом, де і в кого вчився. Значно більше ми знаємо про математичну творчість Евкліда. Перш за все, Евклід є для нас автором "Начал", по яких учились математики всього світу. Ця надзвичайна книга пережила більше двох тисячоліть, але й до цього часу не втратила свого значення не тільки в історії науки, але й у самій математиці. Зміст "Начал" далеко не вичерпується елементарною геометрією - це основи всієї античної математики. Тут підводиться підсумок більш ніж 300-річному її розвитку і разом з тим створюється база для її подальшого розвитку. На геометрії Евкліда базується класична механіка, її апофеозом була поява в 1687 р. "Математичних начал натуральної філософії" Ньютона, де закони земної і небесної механіки і фізики встановлюються в абсолютному евклідовому просторі.

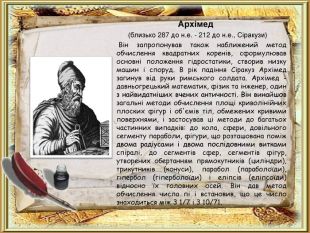
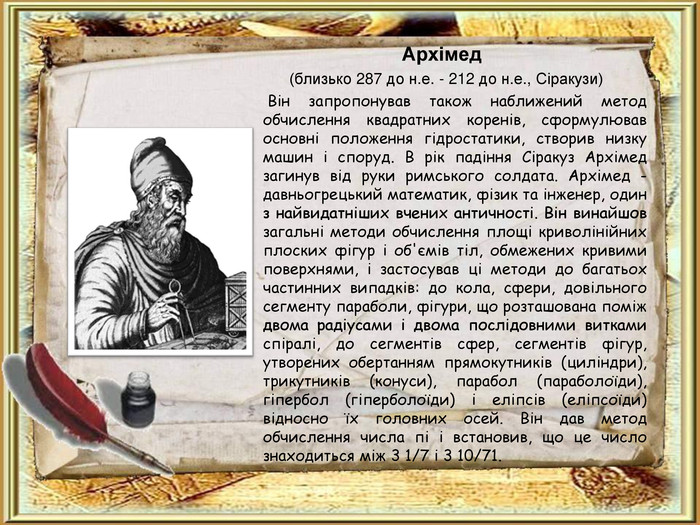
Архімед (близько 287 до н.е. - 212 до н.е., Сіракузи) Він запропонував також наближений метод обчислення квадратних коренів, сформулював основні положення гідростатики, створив низку машин і споруд. В рік падіння Сіракуз Архімед загинув від руки римського солдата. Архімед - давньогрецький математик, фізик та інженер, один з найвидатніших вчених античності. Він винайшов загальні методи обчислення площі криволінійних плоских фігур і об'ємів тіл, обмежених кривими поверхнями, і застосував ці методи до багатьох частинних випадків: до кола, сфери, довільного сегменту параболи, фігури, що розташована поміж двома радіусами і двома послідовними витками спіралі, до сегментів сфер, сегментів фігур, утворених обертанням прямокутників (циліндри), трикутників (конуси), парабол (параболоїди), гіпербол (гіперболоїди) і еліпсів (еліпсоїди) відносно їх головних осей. Він дав метод обчислення числа пі і встановив, що це число знаходиться між 3 1/7 і 3 10/71. 

П'єр Ферма (1601-1665) Видатний французький математик, один із основоположників аналітичної еометрії і теорії чисел, автор робіт в області теорії ймовірностей, оптики, численні нескінченно-малих величин. У 1637 році він сформулював так звану Велику теорему Ферма, яка була доведена американським математиком Ендрю Уайлсом лише у 1995 році. Теорем а стверджує, що для будь-якого натурального n>2 i xyz<>0 рівняння хn+уn=zn не можна розв’язати в цілих (і раціональних) числах.

Микола Іванович Лобачевський (1792-1856) В історію математики М. І. Лобачевський увійшов як перший учений, який виступив з принципово новою теорією геометрії. Тим самим, він завоював собі почесне звання "Копернік геометрії". М.І. Лобачевський зробив сміливий висновок про те, що можлива геометрія, яка грунтується на запереченні аксіоми паралельності Евкліда. Усе життя він присвятив створенню цієї "уявної геометрії", яка зараз називається геометрією Лобачевського. У цій геометрії до даної прямої через дану точку можна провести нескінченно багато прямих, їй паралельних. Це була справжня революція в науці. "Легше було зупинити Сонце, легше було зрушити Землю, ніж звести паралелі до сходження" (В.Ф.Каган) Крім геніальних робіт з геометрії вченому належить ряд важливих праць з алгебри та аналізу. Він запропонував точне визначення функції, довів одну з ознак збіжності рядів, установив відмінність між неперервністю та диференційовністю функції..

Софія Василівна Ковалевська (1850-1891) "В історії людства до Ковалевської не було жінок, рівних їй за силою і своєріднісю математичного таланту" (С.В.Вавілов). Визначний російський математик, письменниця і публіцист. Професор Стокгольмського університету. Авторка праць з математичного аналізу (диференціальні рівняння і аналітичні функції), механіки і астрономії. Перша жінка, яку обрано членом-кореспондентом Петербурзької Академії Наук.

IV.Історичні задачі в шкільному курсі математики Математичні задачі збережені для нас історією дають можливість учням одержати додаткову теоретичну інформацію, допомагають з’ясувати роль і місце математики в практичній діяльності людей, збуджують інтерес та любов до предмету, потяг до самостійної творчості, прояву ініціативи і кмітливості, критичного ставлення до нових фактів. Багато задач, які дійшли до нас із сивої давнини, цікаві не стільки в математичному, скільки в історичному розумінні: вони дають можливість оцінити рівень розвитку математики в різні часи. Такі задачі були поставлені потребами практики і розв’язувалися ще 2000 років до нашої ери, про що свідчать тексти єгипетських папірусів.

Для прикладу розглянемо визначні задачі про геометричні тіла, що доступні для розв’язування учнями, і покажемо їх місце у шкільному курсі стереометрії. Зробимо це за допомогою таблиці, в якій показано, коли в шкільному курсі математики можна використати задачі.

Запропоновані задачі доцільно також використати на уроках повторення та узагальнення знань. Оскільки задачі різної складності, то вчитель матиме можливість здійснювати рівневу диференціацію на такому уроці. Перед (або після) розв’язуванням задачі корисно дати історичну довідку. Це вчитель може зробити сам або доручити учневі, порекомендувавши відповідну літературу.

V.Використання історичних відомостей у позакласній роботі Великі можливості для знайомства з елементами історії математики відкриваються перед учнями на позакласних заняттях. Це робота в математичних гуртках, самостійна робота з додатковою літературою для написання рефератів, виступи здоповідями перед молодшими школярами, розв’язування цікавих історичних задач тощо. Спеціальні розділи з історії математики включено до програми факультативних занять з математики в основній школі. Вчителі можуть розглядати ці теми і на гуртках чи інших позакласних заняттях.

Для ефективної організації позакласної роботи з вивчення елементів історії математики доцільно використовувати доступну навчальну і популярну літературу. Незамінним помічником у цьому кожному вчителю і учню може стати український науково-методичний журнал “У світі математики”.

Виступи учнів з історико - математичними повідомленнями не тільки розширюють їх математичні знання, розвивають загальну ерудицію, але й викликають інтерес до навчального предмету, що позитивно впливає на засвоєння програмного матеріалу. Наведемо декілька тем рефератів, які можна запропонувати учням загальноосвітніх шкіл: Нумерації та історії їх виникнення; Прості числа та решето Ератосфена; Золотий перерізта його використання; Фалес Мілетський і теорема Фалеса; Школа Піфагора; Архімед у легендах і дійсності; Омар Хайям – математик і поет; М. В. Остроградський – математик світової величини.

Традиційною формою організації позакласної роботи з математики в школі є математичні вечори. Прикрасою кожного вечора можуть стати історичні цікавинки, старовинні задачі, вікторини тощо.

Дякую за увагу!!!