Презентація "Візуальні опори до скрайб-презентацій з математики"

Ретроспективавізуальних опор з математики. Огляд досвіду використання візуальних опор до скрайб-презентацій з метою переосмислення і удосконалення уроків математики. Учитель математики Ляшко О. І.

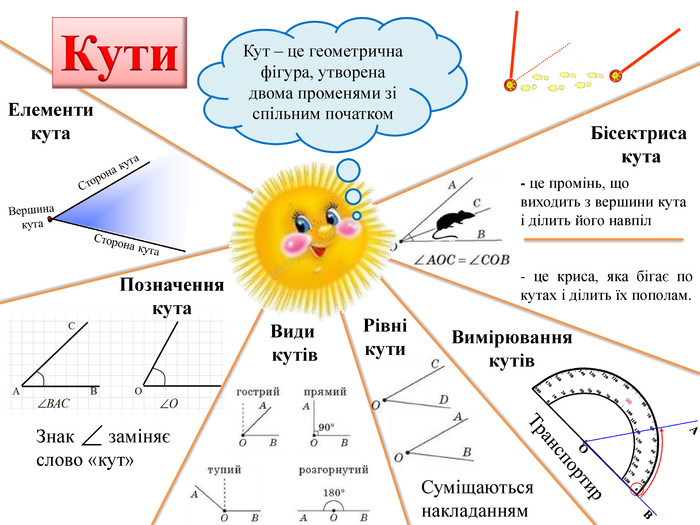
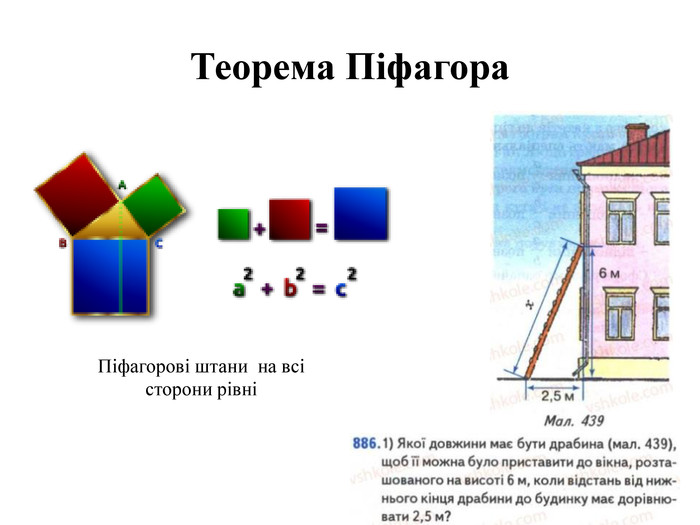
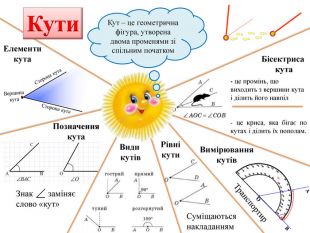
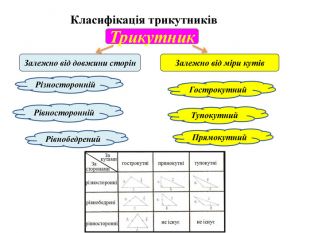
Знак заміняєслово «кут»Позначеннякута. Види кутів. Елементикута. Рівнікути. Суміщаються накладанням. Бісектриса кута- це промінь, що виходить з вершини кута і ділить його навпіл- це криса, яка бігає по кутах і ділить їх пополам. Вимірюваннякутів. Транспортир. Кут – це геометрична фігура, утворена двома променями зі спільним початком. Кути

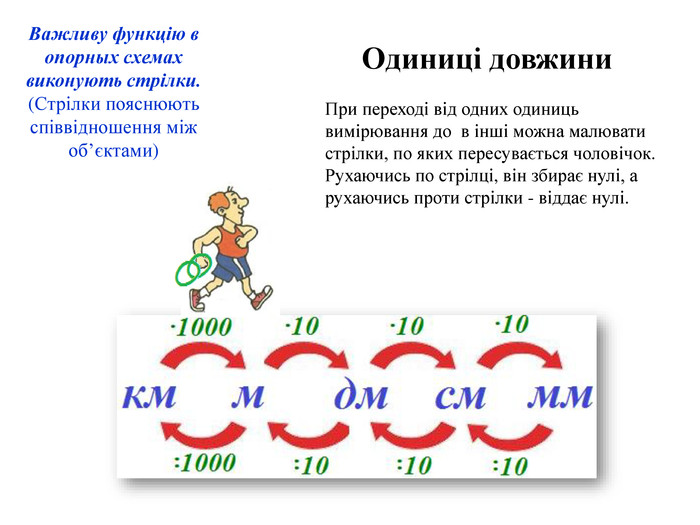
Одиниці довжини При переході від одних одиниць вимірювання до в інші можна малювати стрілки, по яких пересувається чоловічок. Рухаючись по стрілці, він збирає нулі, а рухаючись проти стрілки - віддає нулі. Важливу функцію в опорных схемах виконують стрілки.(Стрілки пояснюють співвідношення між об’єктами)

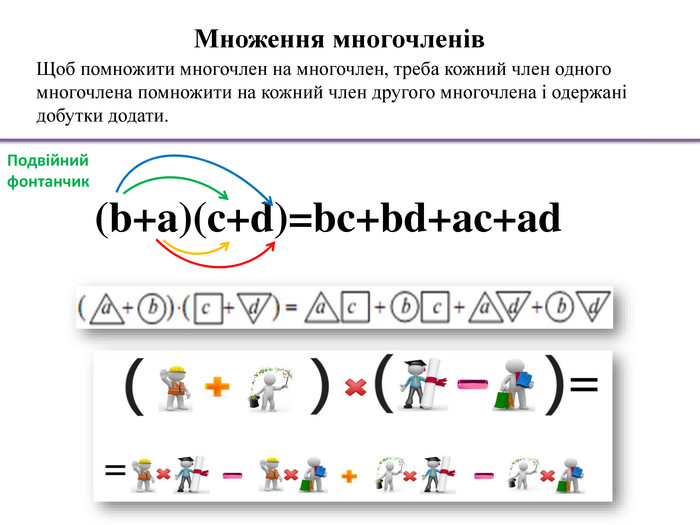
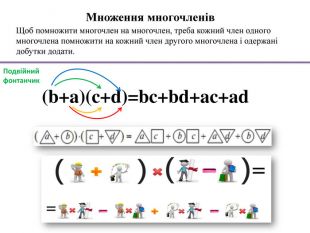
Множення одночлена на многочлен. Щоб помножити одночлен на многочлен, треба одночлен помножити на кожний член многочлена й одержані добутки додати. Тобто множення одночлена на многочлен здійснюється на основі розподільної властивості множення. Троє друзі живуть в прекрасному будинку і в гості до них завітав їх товариш. Якщо товариш вихований, то він повинен привітатися з кожним із друзів. Роздати всім морозиво Мама-пташка годує кожне своє пташеняa(b+c)=ad+ac. Життєві ситуації допомагають зрозуміти математичні правила. Особливу роль відіграють чоловічки, які дозволяють моделювати різноманітні ситуації. Особливу роль відіграють ….. стрілочки Фонтанчик

Множення многочленів(b+a)(c+d)=bc+bd+ac+ad. Щоб помножити многочлен на многочлен, треба кожний член одного многочлена помножити на кожний член другого многочлена і одержані добутки додати. Подвійний фонтанчик

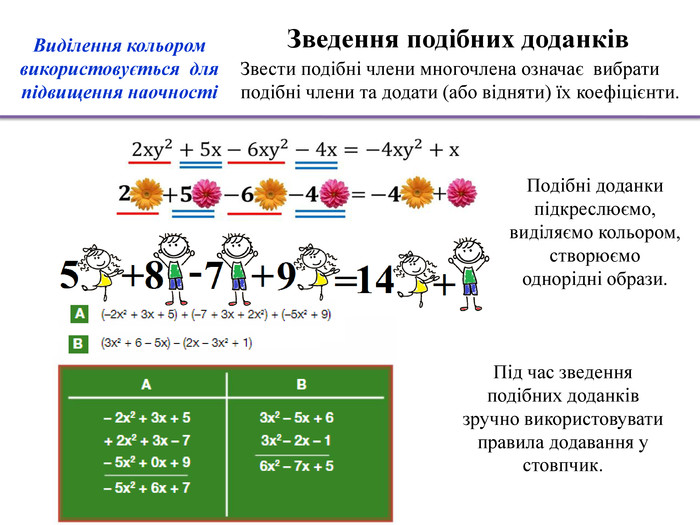
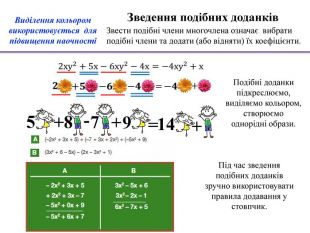
Звести подібні члени многочлена означає вибрати подібні члени та додати (або відняти) їх коефіцієнти. Зведення подібних доданків. Під час зведення подібних доданків зручно використовувати правила додавання у стовпчик. Подібні доданкипідкреслюємо, виділяємо кольором, створюємо однорідні образи. Виділення кольором використовується для підвищення наочності

Розкриття дужок. Метод фонетичних асоціацій Знак «мінус» перед дужкою уміє говорити, і він каже: «Міняй»; причому легко запам'ятати, тому що слово починається з тієї ж букви, що і знак «Мінус» Мінус - Міняй! Плюс – переписуй!Щоб розкрити дужки, перед якими стоїть знак «+», потрібно опустити дужки і знак «+», що стоїть перед ними, та записати всі доданки, які були в дужках, зі своїми знаками. а + (b - с) = а + b - с. Щоб розкрити дужки, перед якими стоїть знак «-», потрібно опустити дужки і знак «-», що стоїть перед ними, і записати всі доданки, які були в дужках, із протилежними знаками. а - (b - с) = а - b + с.

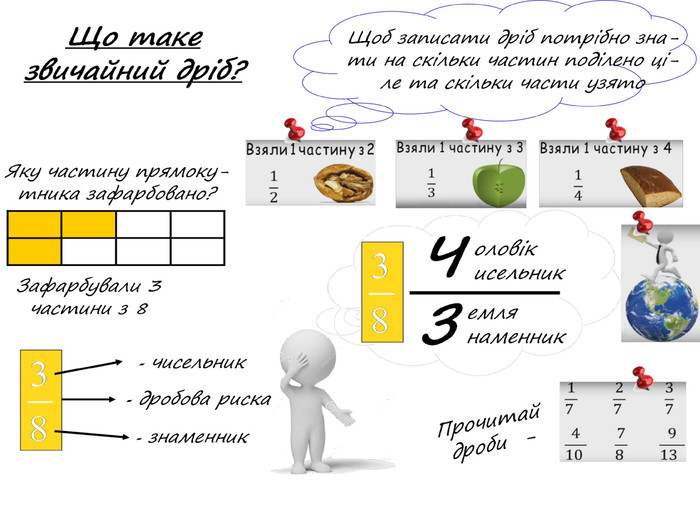
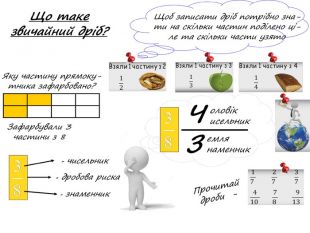
Звичайні дроби. Звичайні дроби записують за допомогою двох натуральних чисел і риски дробу (дробової риски)Число, що стоїть над рискою дробу, називається чисельником. Число, що стоїть під рискою дробу, називається знаменником. Знаменник дробу показує на скільки рівних частин поділили щось ціле, а чисельник – скільки таких частин взяли. Де знаходиться чисельник дробу, а де знаменник?«Людина подібна до дробу: у знаменнику – те, що вона про себе думає, у чисельнику – те, ким вона є насправді. Чим більший знаменник, тим менший дріб». Лев Миколайович Толстой. Знаменник, назва якого починається на букву «з» з довгим хвостиком. Щоб дробова риска їй не заважала, «з» знаходиться внизу, а буква «ч» - нагорі.

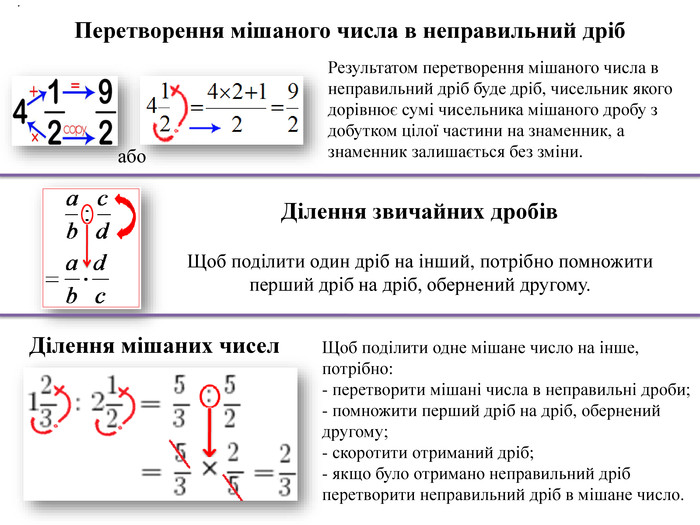
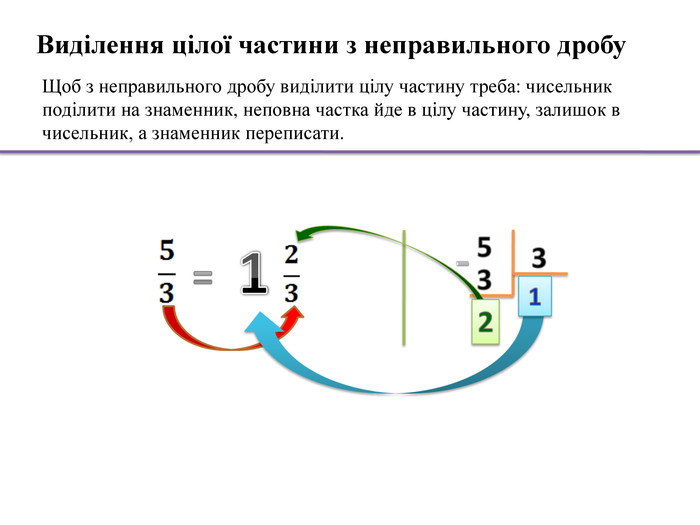
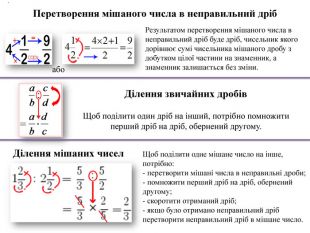
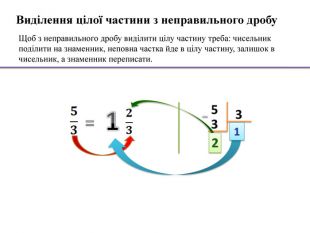
Ділення звичайних дробів. Щоб поділити один дріб на інший, потрібно помножити перший дріб на дріб, обернений другому. Ділення мішаних чисел. Щоб поділити одне мішане число на інше, потрібно:- перетворити мішані числа в неправильні дроби; помножити перший дріб на дріб, обернений другому; скоротити отриманий дріб;- якщо було отримано неправильний дріб перетворити неправильний дріб в мішане число. . Результатом перетворення мішаного числа в неправильний дріб буде дріб, чисельник якого дорівнює сумі чисельника мішаного дробу з добутком цілої частини на знаменник, а знаменник залишається без зміни. Перетворення мішаного числа в неправильний дрібабо

Щоб з неправильного дробу виділити цілу частину треба: чисельник поділити на знаменник, неповна частка йде в цілу частину, залишок в чисельник, а знаменник переписати. Виділення цілої частини з неправильного дробу

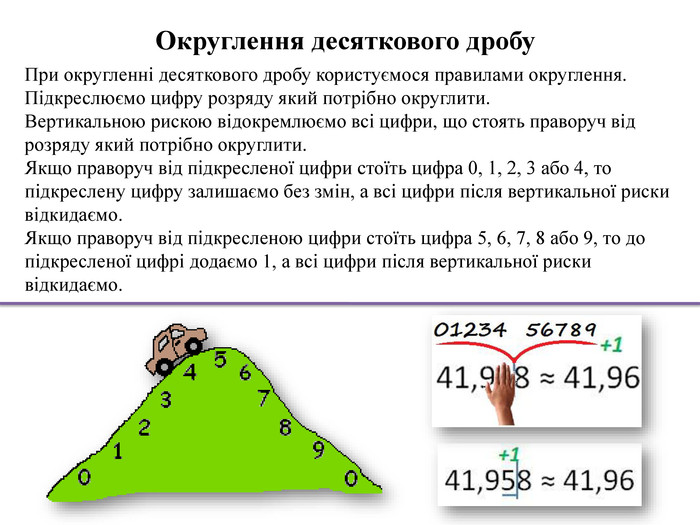
Округлення десяткового дробу. При округленні десяткового дробу користуємося правилами округлення. Підкреслюємо цифру розряду який потрібно округлити. Вертикальною рискою відокремлюємо всі цифри, що стоять праворуч від розряду який потрібно округлити. Якщо праворуч від підкресленої цифри стоїть цифра 0, 1, 2, 3 або 4, то підкреслену цифру залишаємо без змін, а всі цифри після вертикальної риски відкидаємо. Якщо праворуч від підкресленою цифри стоїть цифра 5, 6, 7, 8 або 9, то до підкресленої цифрі додаємо 1, а всі цифри після вертикальної риски відкидаємо.

Множення і ділення додатних і від’ємних чисел. Математичні знака « + » і «- » прийшли до нас із країн Сходу. Арабські вчені, виводячи правила дій з додатними і від'ємними числами, користувалися такими цікавими аналогіями:«Друг мого друга – мій друг» «Ворог мого ворога - мій друг»«Друг мого ворога – мій ворог»«Ворог мого друга – мій ворог» Якщо чоловічок моргає, то в результаті буде мінус. Різні знаки – від'ємне число. Щоб помножити два числа з різними знаками, треба помножити їх модулі і перед отриманим добутком поставити знак “-”. Щоб помножити два від’ємних числа, треба помножити їх модулі. Щоб поділити одне раціональне число на друге, треба поділити їх модулі; якщо знаки діленого і дільника різні, то перед результатом слід поставити знак мінус. Правила знаків

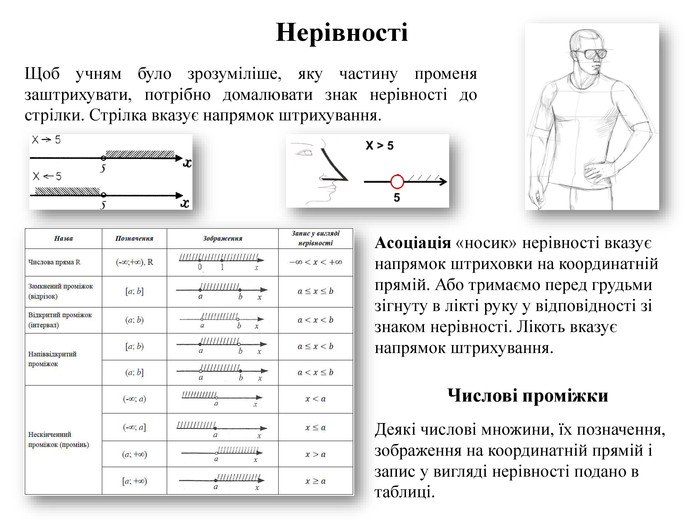
Асоціація «носик» нерівності вказує напрямок штриховки на координатній прямій. Або тримаємо перед грудьми зігнуту в лікті руку у відповідності зі знаком нерівності. Лікоть вказує напрямок штрихування. Щоб учням було зрозуміліше, яку частину променя заштрихувати, потрібно домалювати знак нерівності до стрілки. Стрілка вказує напрямок штрихування. НерівностіЧислові проміжки. Деякі числові множини, їх позначення, зображення на координатній прямій і запис у вигляді нерівності подано в таблиці.

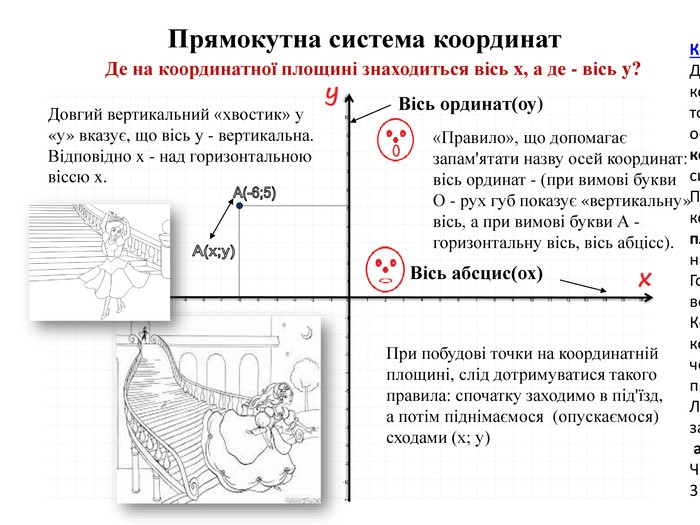
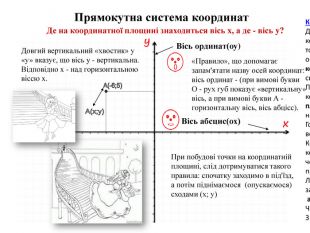
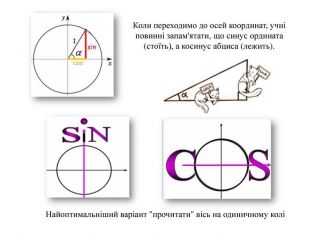
Вісь абсцис(ох)Вісь ординат(оу)А(-6;5)А(х;у)Де на координатної площині знаходиться вісь x, а де - вісь y?Прямокутна система координат«Правило», що допомагає запам'ятати назву осей координат: вісь ординат - (при вимові букви О - рух губ показує «вертикальну» вісь, а при вимові букви А - горизонтальну вісь, вісь абцісс). Довгий вертикальний «хвостик» у «у» вказує, що вісь y - вертикальна. Відповідно x - над горизонтальною віссю x. При побудові точки на координатній площині, слід дотримуватися такого правила: спочатку заходимо в під'їзд, а потім піднімаємося (опускаємося) сходами (х; у)Координатная плоскость. Две взаимно перпендикулярные координатные прямые, пересекающиеся в точке О — начале отсчета, образуют прямоугольную систему координат, называемую также декартовой системой координат. Плоскость, на которой выбрана система координат, называется координатной плоскостью. Координатные прямые называются координатными осями. Горизонтальная — ось абсцисс (Ох), вертикальная — ось ординат (Оy). Координатные оси разбивают координатную плоскость на четыре части — четверти. Порядковые номера четвертей принято считать  против часовой стрелки. Любая точка в координатной плоскости задается своими координатами — абсциссой и ординатой. Например, А(3; 4). Читают: точка А с координатами 3 и 4. Здесь 3 — абсцисса, 4 — ордината.

«Число π запам’ятай – три чотирнадцять підставляй!» «Хто по колу піде, той довжину кола знайде» «Довжина кола відтепер, буде рівна 2πr» «Площу круга треба знати: добуток πr в квадраті!»Мнемонічні фрази Довжина кола. Площа круга.

Класифікація трикутників. Трикутник. Залежно від довжини сторін. Залежно від міри кутів. Різносторонній. Рівносторонній. Рівнобедрений. Гострокутний. Тупокутний. Прямокутний

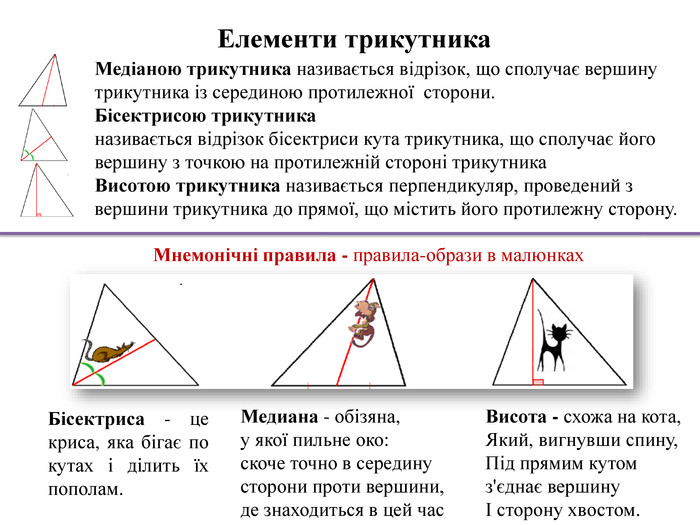
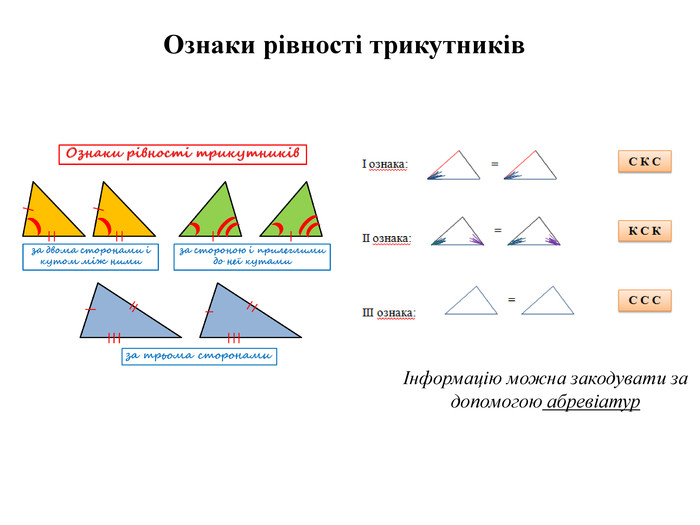
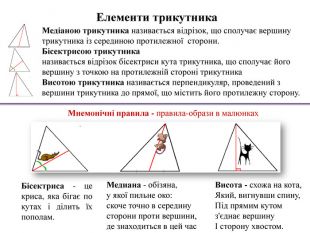
Медіаною трикутника називається відрізок, що сполучає вершину трикутника із серединою протилежної сторони. Бісектрисою трикутниканазивається відрізок бісектриси кута трикутника, що сполучає його вершину з точкою на протилежній стороні трикутника. Висотою трикутника називається перпендикуляр, проведений з вершини трикутника до прямої, що містить його протилежну сторону. Висота - схожа на кота,Який, вигнувши спину,Під прямим кутомз'єднає вершинуІ сторону хвостом. Мнемонічні правила - правила-образи в малюнках. Бісектриса - це криса, яка бігає по кутах і ділить їх пополам. Медиана - обізяна, у якої пильне око: скоче точно в середину сторони проти вершини, де знаходиться в цей час. Елементи трикутника

Прямокутний трикутник. Метод фонетичних асоціацій - знаходження співзвучних асоціацій до слів. Цей метод використовую, для запам’ятовування термінів, назв, правил. Катет – котик Гіпотенуза – гіпопотам. Катети – це сторони, що утворюють прямий кут, а гіпотенуза – це сторона, яка лежить напротив прямого кута. Асоціація. Якщо порівняти назви сторін прямокутного трикутника: «катет», «гіпотенуза», то бачимо, що слово «гіпотенуза» довше слово ніж «катет». Так і в трикутнику: гіпотенуза - найдовша сторона. Отже, асоціація: Катет - коротке слово, коротка сторона. Гіпотенуза - довге слово, найдовша з сторін. Запам'ятати де катет, а де гіпотенуза, і не переплутати їх, допоможуть:

Кольорова асоціація. Запам'ятовування матеріалу полегшується за рахунок підключення зорової пам'яті. Частина сигналів може бути забарвлена в яскраві кольори. Запам'ятати співвідношення, що зв'язують пропорційні відрізки в прямокутному трикутнику, допомагає кольорова асоціація. Якщо виділити кожну пару - катет і його проекцію на гіпотенузу - одним кольором, запам'ятати пропорційні відрізки в прямокутному трикутнику можна швидко і легко. Пропорційні відрізки в прямокутному трикутнику. Висота прямокутного трикутника, проведена до гіпотенузи, ділить її на відрізки, які називаються проекціями катетів на гіпотенузу. Властивості прямокутного трикутника:1. Висота, проведена до гіпотенузи, є середнім пропорційним між проекціями катетів на гіпотенузу.2. Катет є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу

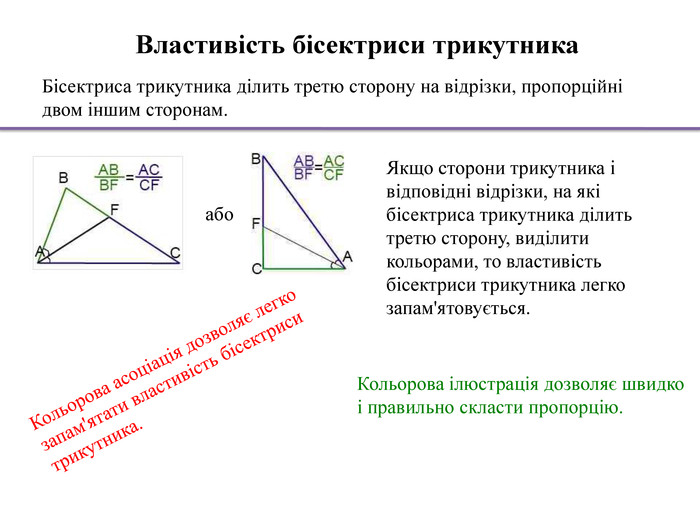
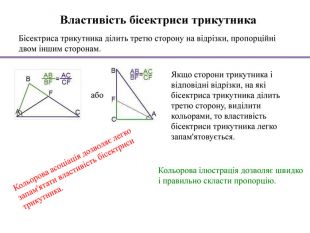
Кольорова ілюстрація дозволяє швидко і правильно скласти пропорцію. Якщо сторони трикутника і відповідні відрізки, на які бісектриса трикутника ділить третю сторону, виділити кольорами, то властивість бісектриси трикутника легко запам'ятовується.або. Кольорова асоціація дозволяє легко запам'ятати властивість бісектриси трикутника. Бісектриса трикутника ділить третю сторону на відрізки, пропорційні двом іншим сторонам. Властивість бісектриси трикутника

Ознаки рівності трикутниківІнформацію можна закодувати за допомогою абревіатур

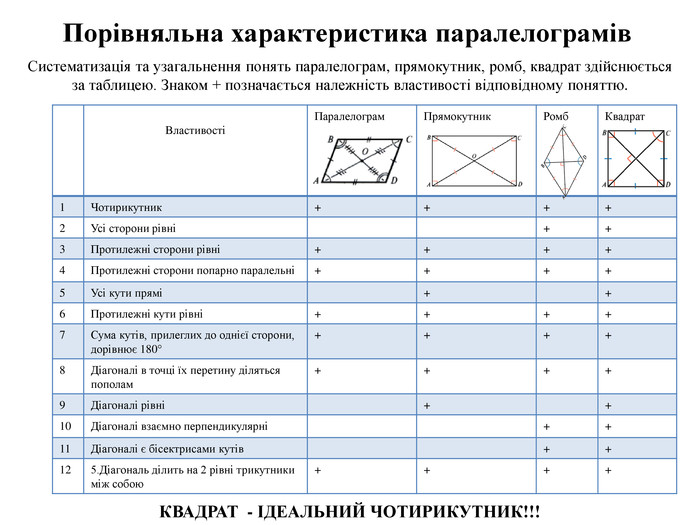
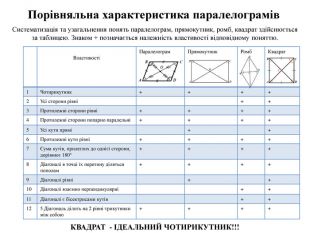
КВАДРАТ - ІДЕАЛЬНИЙ ЧОТИРИКУТНИК!!!{BC89 EF96-8 CEA-46 FF-86 C4-4 CE0 E7609802}ВластивостіПаралелограм. Прямокутник. Ромб. Квадрат1 Чотирикутник++++2 Усі сторони рівні++3 Протилежні сторони рівні ++++4 Протилежні сторони попарно паралельні ++++5 Усі кути прямі++6 Протилежні кути рівні ++++7 Сума кутів, прилеглих до однієї сторони, дорівнює 180° ++++8 Діагоналі в точці їх перетину діляться пополам ++++9 Діагоналі рівні ++10 Діагоналі взаємно перпендикулярні++11 Діагоналі є бісектрисами кутів++125. Діагональ ділить на 2 рівні трикутники між собою++++Систематизація та узагальнення понять паралелограм, прямокутник, ромб, квадрат здійснюється за таблицею. Знаком + позначається належність властивості відповідному поняттю. Порівняльна характеристика паралелограмів

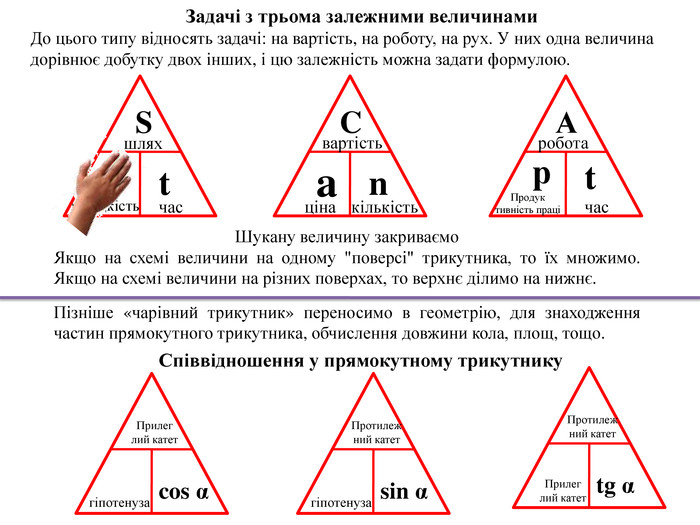
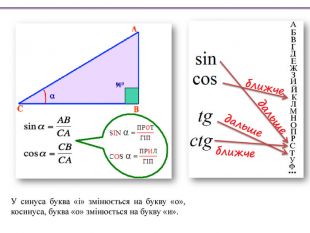
Шукану величину закриваємо. Якщо на схемі величини на одному "поверсі" трикутника, то їх множимо. Якщо на схемі величини на різних поверхах, то верхнє ділимо на нижнє. Пізніше «чарівний трикутник» переносимо в геометрію, для знаходження частин прямокутного трикутника, обчислення довжини кола, площ, тощо. St. Vшляхшвидкістьчас. Cnaвартістьцінакількість. Аtрробота. Продуктивність працічасsin α гіпотенуза. Протилежний катетtg α Прилеглий катет. Протилежний катетcos α Прилеглий катетгіпотенуза. Співвідношення у прямокутному трикутнику. Задачі з трьома залежними величинами. До цього типу відносять задачі: на вартість, на роботу, на рух. У них одна величина дорівнює добутку двох інших, і цю залежність можна задати формулою.

Теорема Піфагора. Піфагорові штани на всі сторони рівні

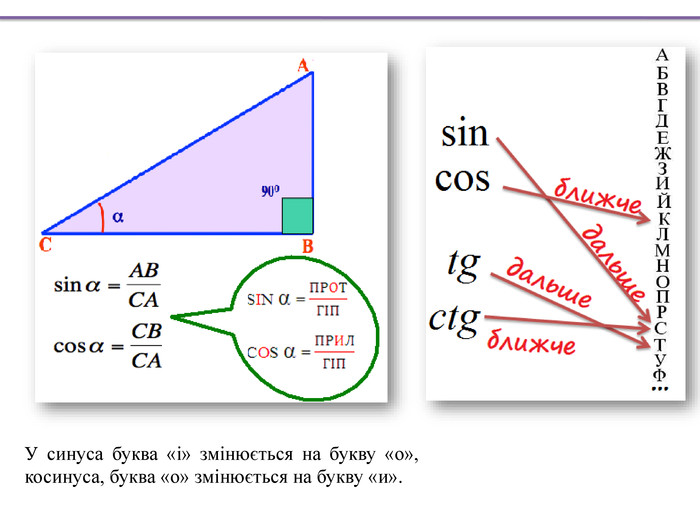
«Синус кута»: в перекладі з англійського слово «see» озачає «бачу, бачити, дивитися». Отже, в учнів з'явитися звукова асоціація. Сприйняття йде через слух - співзвуччя з самим словом "синус", також візуально: малюємо око і "дивимося" - показуючи стрілкою напрямок погляду.«Косинус кута»: так як у відношенні необхідно брати прилеглий до гіпотенузи катет, то зобразимо прилеглий катет - прилеглу людину. Співвідношення між сторонами і кутами прямокутного трикутника Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до гіпотенузи. Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи. Тангенсом гострого кута прямокутного трикутника називається відношення протилежного катета до прилеглого.

У синуса буква «і» змінюється на букву «о», косинуса, буква «о» змінюється на букву «и».

Найоптимальніший варіант "прочитати" вісь на одиничному коліКоли переходимо до осей координат, учні повинні запам'ятати, що синус ордината (стоїть), а косинус абциса (лежить).

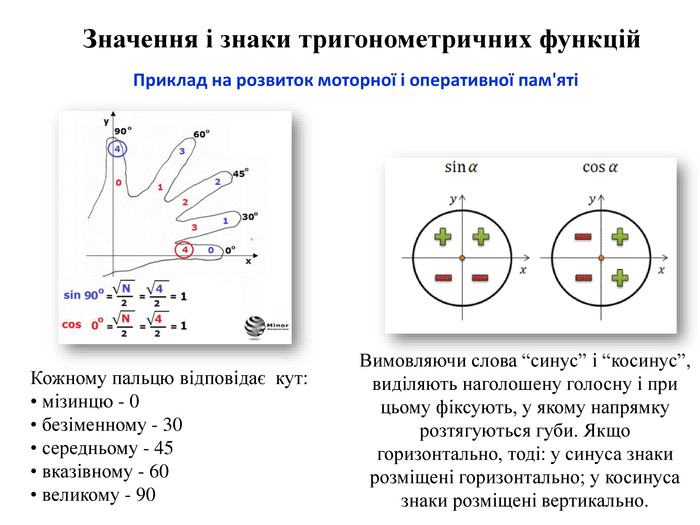
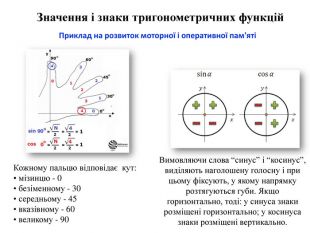
Значення і знаки тригонометричних функцій. Вимовляючи слова “синус” і “косинус”, виділяють наголошену голосну і при цьому фіксують, у якому напрямку розтягуються губи. Якщо горизонтально, тоді: у синуса знаки розміщені горизонтально; у косинуса знаки розміщені вертикально. Приклад на розвиток моторної і оперативної пам'ятіКожному пальцю відповідає кут:• мізинцю - 0• безіменному - 30• середньому - 45• вказівному - 60• великому - 90

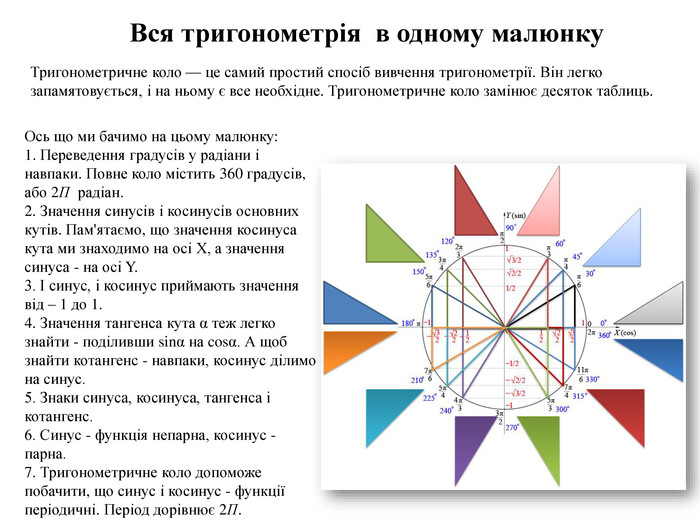
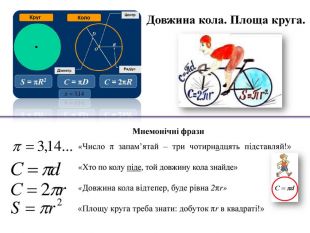
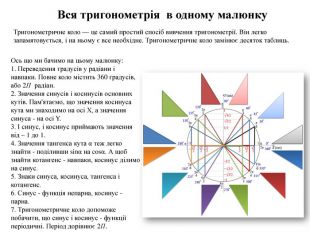
Тригонометричне коло — це самий простий спосіб вивчення тригонометрії. Він легко запамятовується, і на ньому є все необхідне. Тригонометричне коло замінює десяток таблиць. Вся тригонометрія в одному малюнку. Ось що ми бачимо на цьому малюнку:1. Переведення градусів у радіани і навпаки. Повне коло містить 360 градусів, або 2 П радіан.2. Значення синусів і косинусів основних кутів. Пам'ятаємо, що значення косинуса кута ми знаходимо на осі Х, а значення синуса - на осі Y.3. І синус, і косинус приймають значення від – 1 до 1.4. Значення тангенса кута α теж легко знайти - поділивши sinα на cosα. А щоб знайти котангенс - навпаки, косинус ділимо на синус.5. Знаки синуса, косинуса, тангенса і котангенс.6. Синус - функція непарна, косинус - парна.7. Тригонометричне коло допоможе побачити, що синус і косинус - функції періодичні. Період дорівнює 2 П.

З усіх основних тригонометричних функцій, тільки у = cosх є парною функцією. Опора - «Панда». По-перше звукова - «па», по-друге зорову: cos (- x) = cos x. При цьому додамо «панда голодний», тому що «з'їдає» знак «мінус». «Годуємо» функцію. Косинус - функція парна; синус, тангенс і котангенс - непарні. Властивості «парності – непарності» тригонометричних функцій

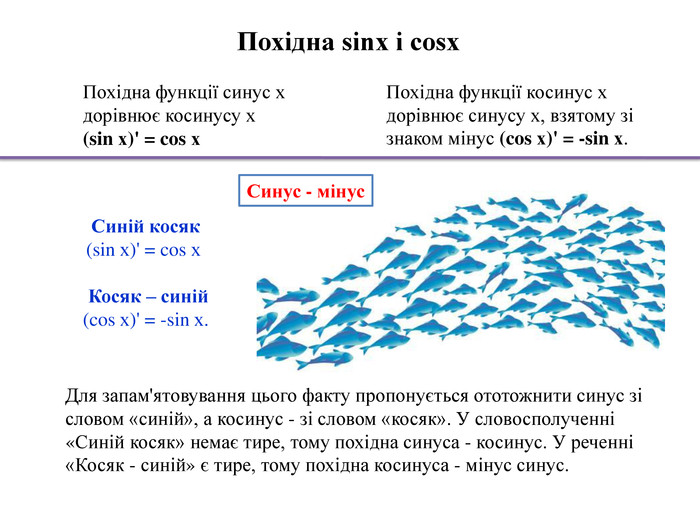
Похідна sinх і cosх. Похідна функції косинус х дорівнює синусу х, взятому зі знаком мінус (cos х)' = -sin х. Синій косяк(sin х)' = cos х  Косяк – синій(cos х)' = -sin х. Для запам'ятовування цього факту пропонується ототожнити синус зі словом «синій», а косинус - зі словом «косяк». У словосполученні «Синій косяк» немає тире, тому похідна синуса - косинус. У реченні «Косяк - синій» є тире, тому похідна косинуса - мінус синус. Похідна функції синус х дорівнює косинусу х (sin х)' = cos х Синус - мінус

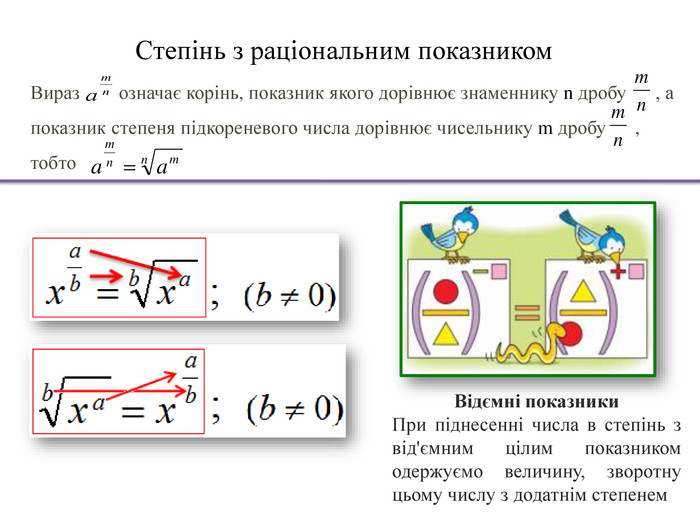
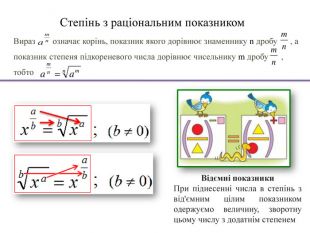
Степінь з раціональним показником. Вираз   означає корінь, показник якого дорівнює знаменнику n дробу  , апоказник степеня підкореневого числа дорівнює чисельнику m дробу  , тобто. Відємні показники. При піднесенні числа в степінь з від'ємним цілим показником одержуємо величину, зворотну цьому числу з додатнім степенем

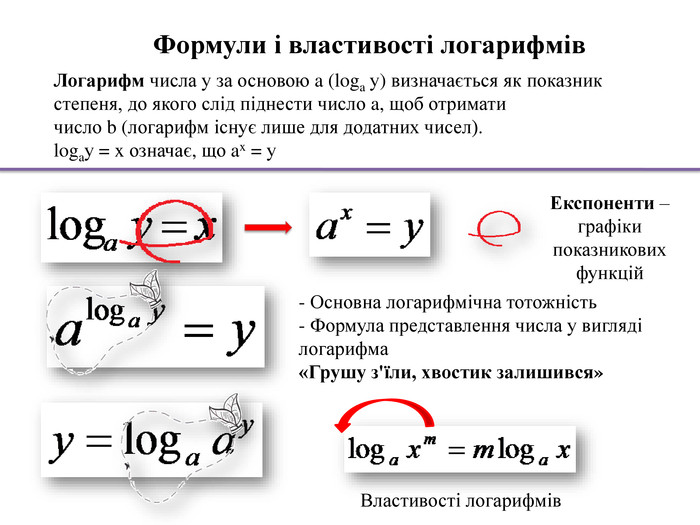
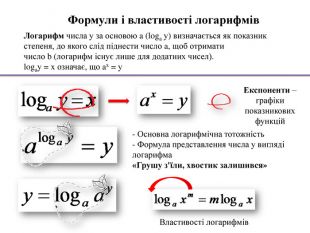
Логарифм числа у за основою a (loga у) визначається як показник степеня, до якого слід піднести число a, щоб отримати число b (логарифм існує лише для додатних чисел). logaу = x означає, що ax = у. Формули і властивості логарифмів- Основна логарифмічна тотожність- Формула представлення числа у вигляді логарифма  «Грушу з'їли, хвостик залишився»Експоненти – графіки показникових функцій. Властивості логарифмів

Класи. Розряди

Те, що сам ти знаєш, передай іншим, а те, чого не знаєш, від інших візьми. Анварі