Презентація з алгебри та початків аналізу у 11-му класі на тему: " Визначений інтеграл та його застосування"
Про матеріал
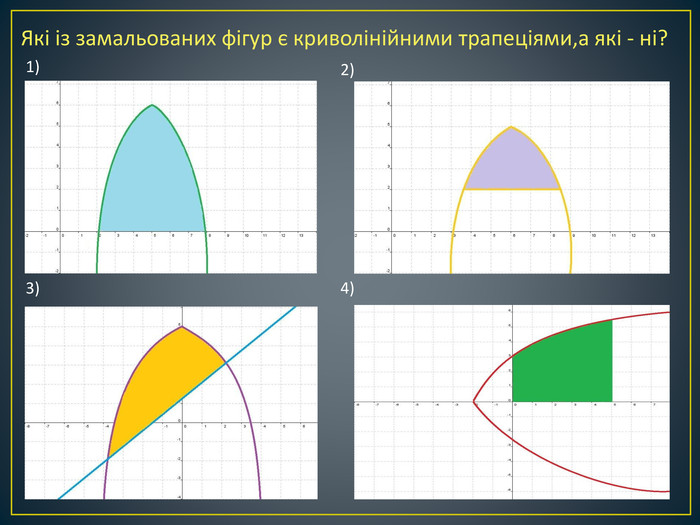
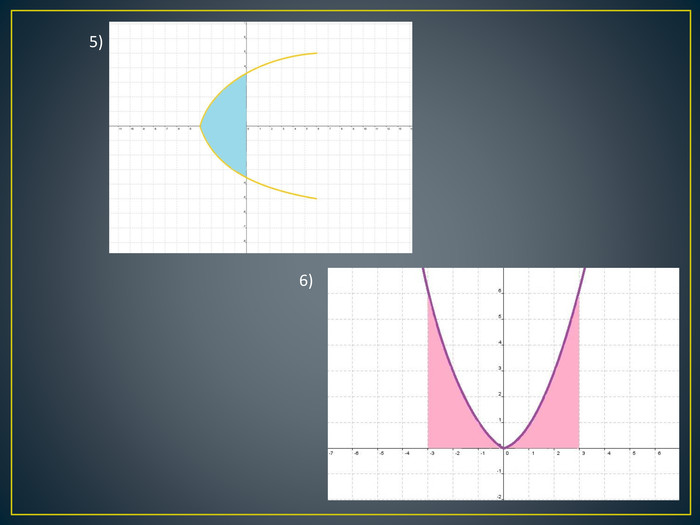
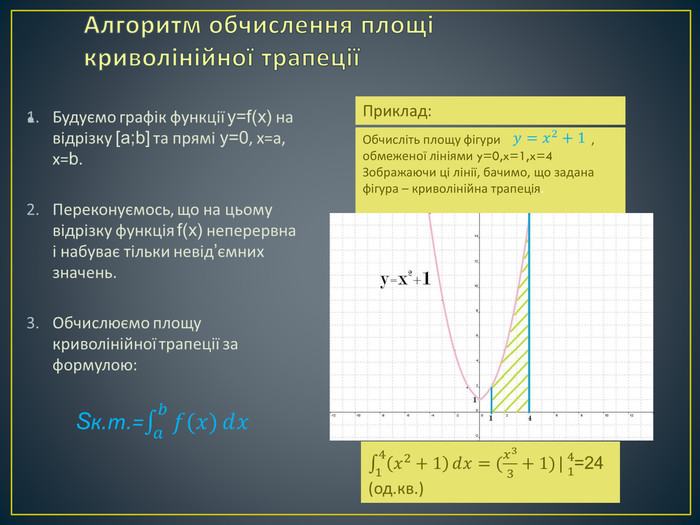
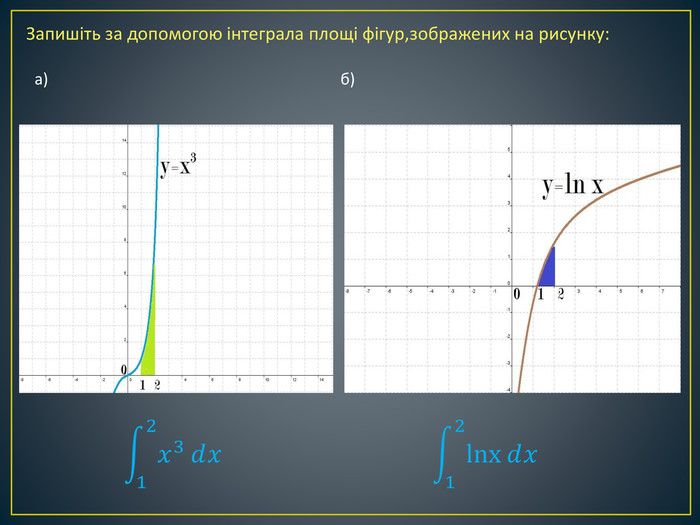
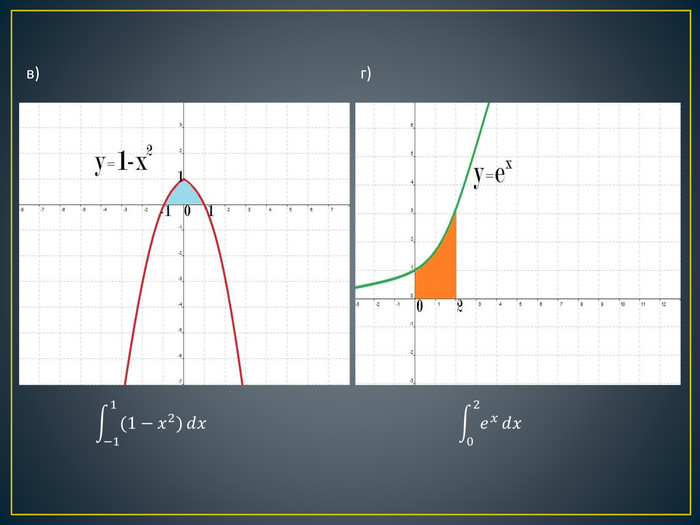
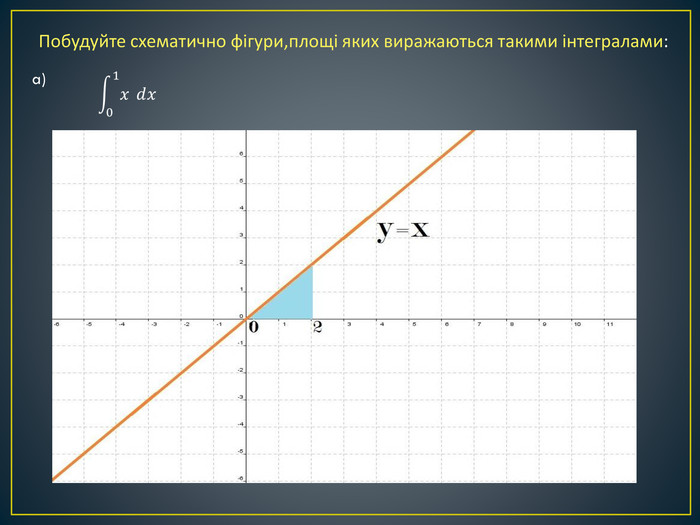
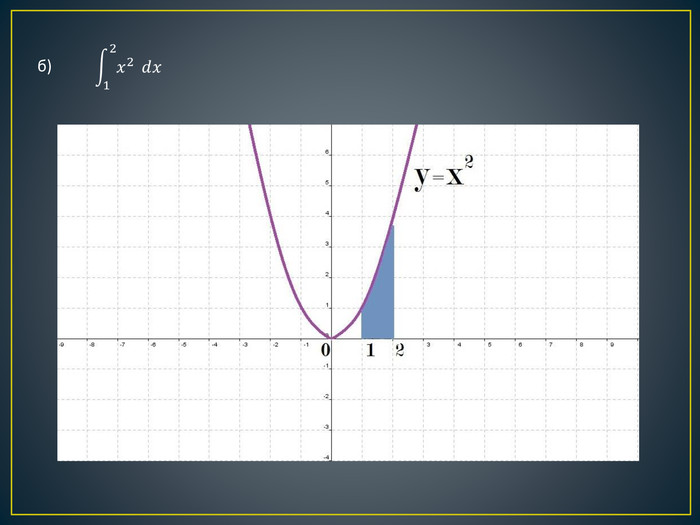
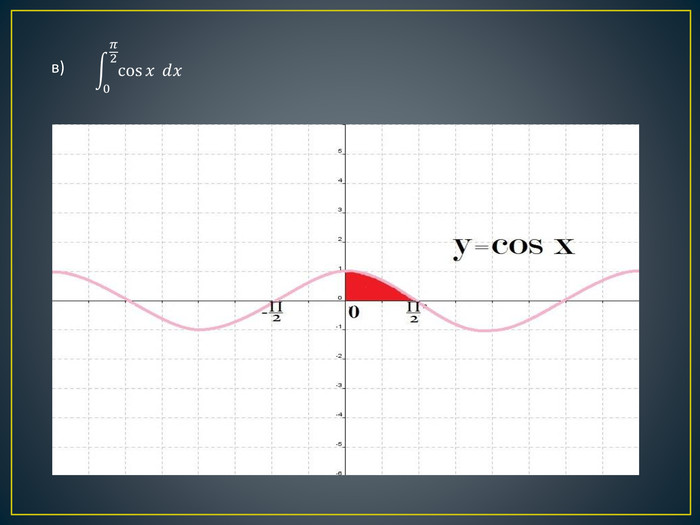
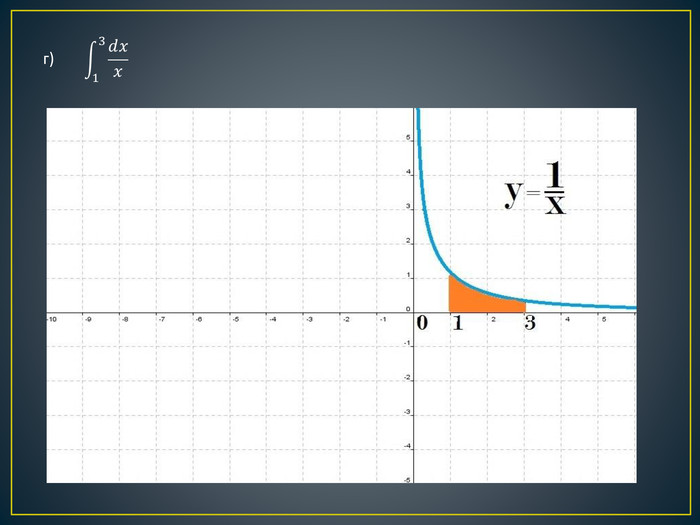
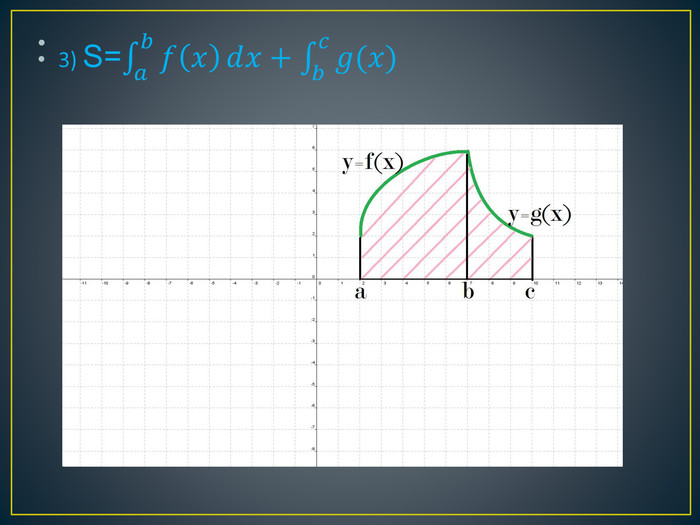
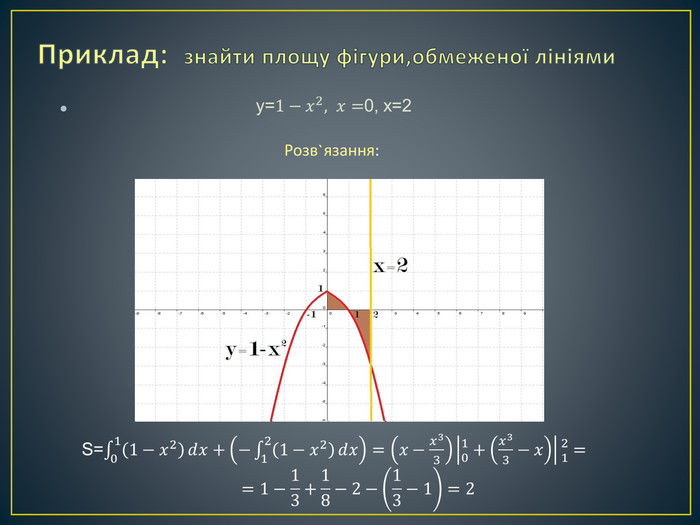
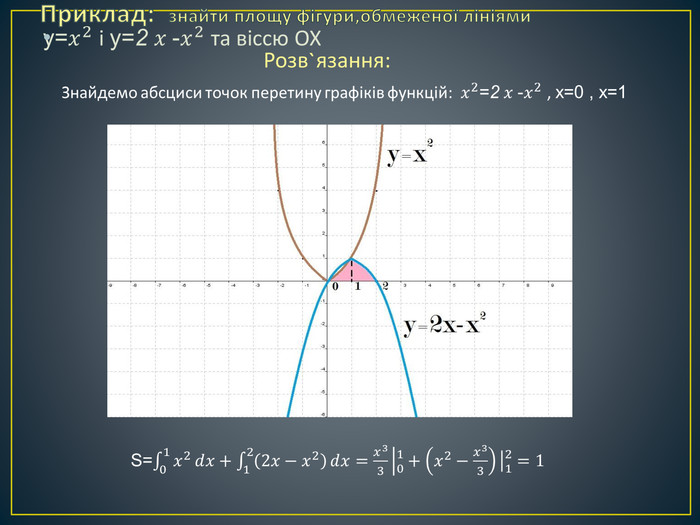
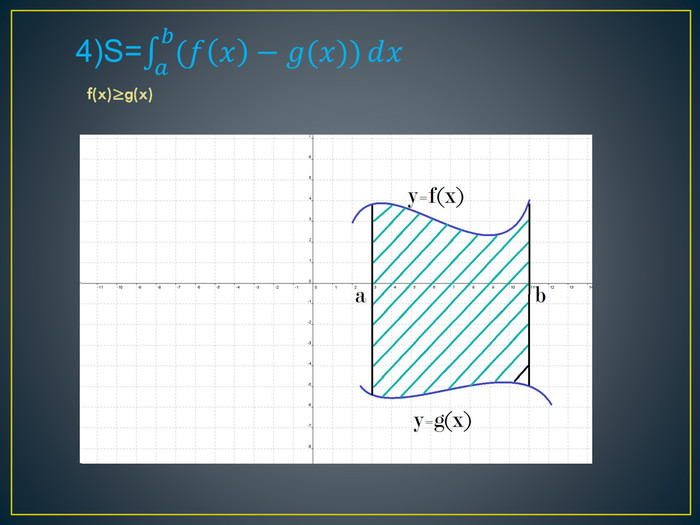
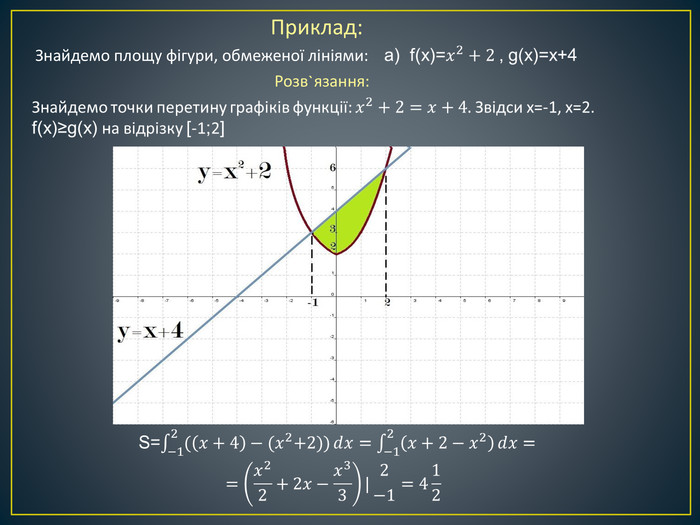
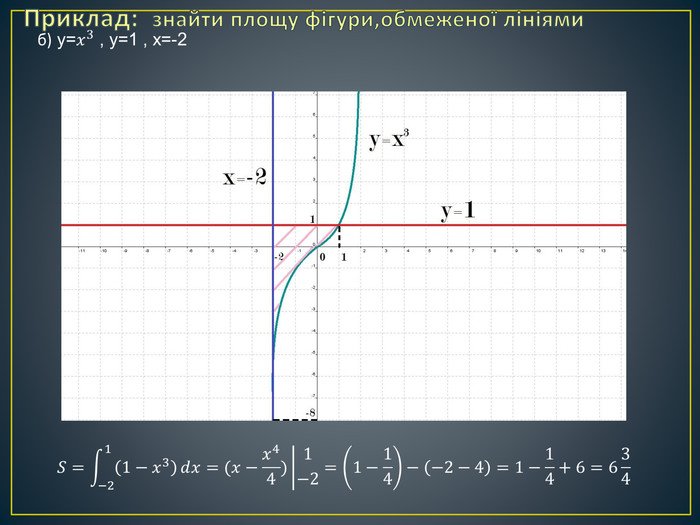
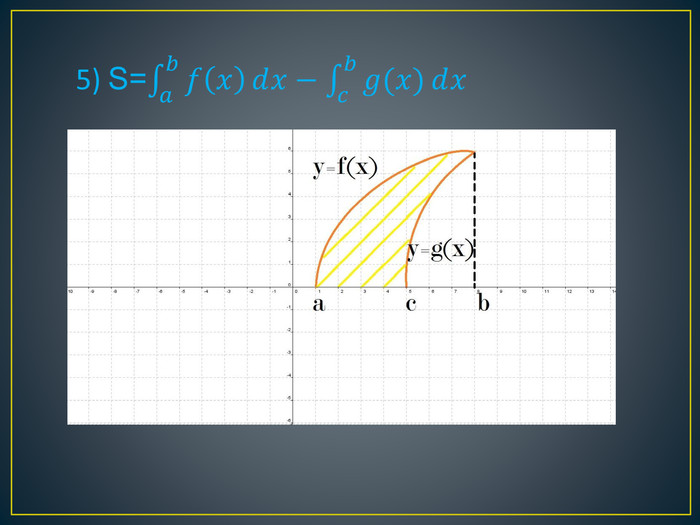
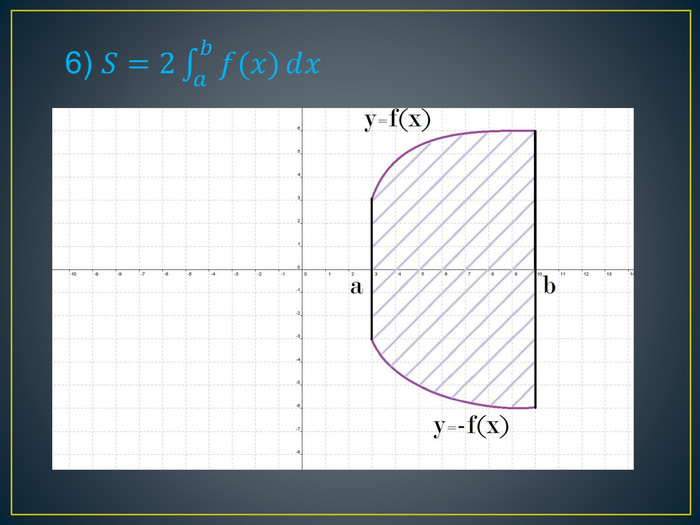
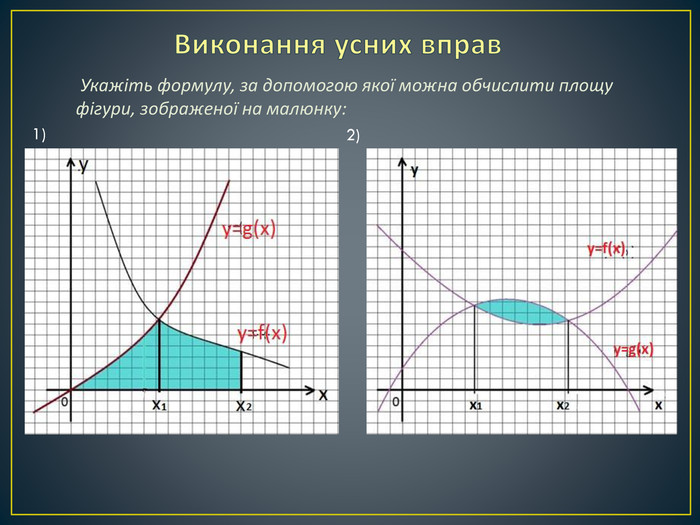
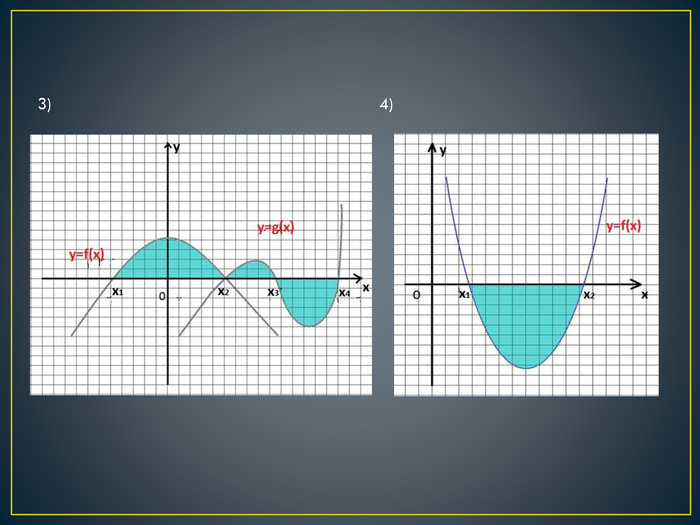
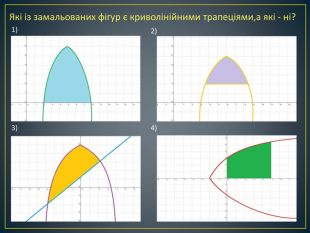
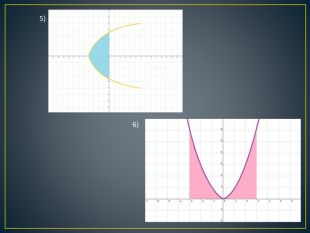
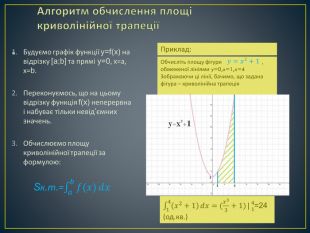
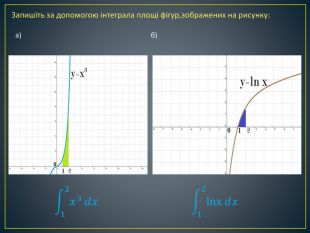
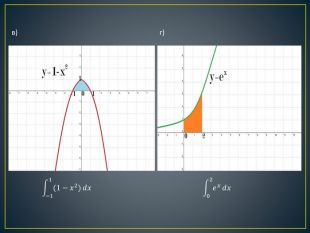
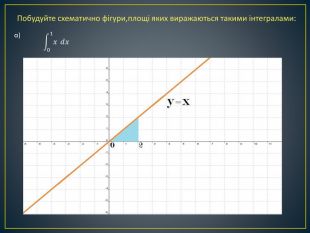
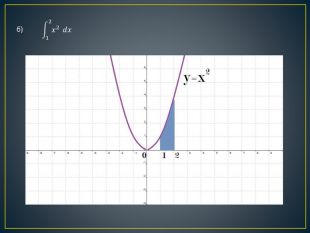
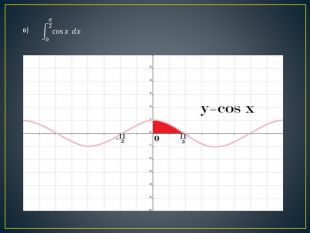
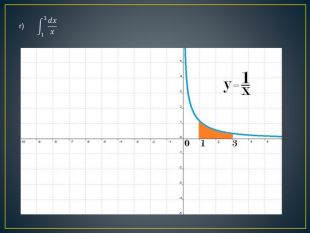
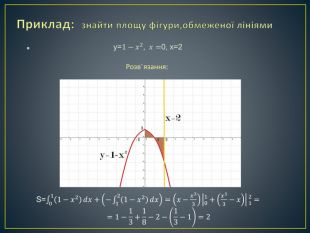
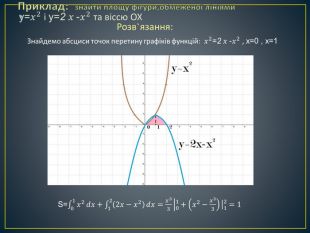
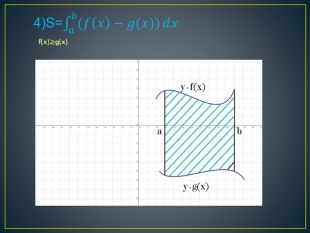
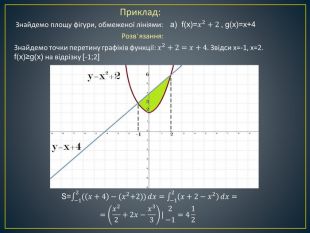
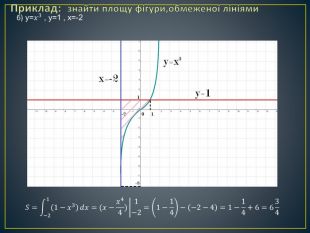
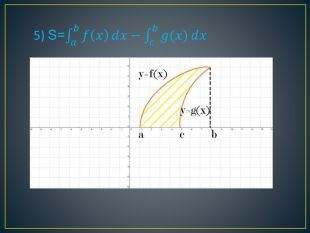
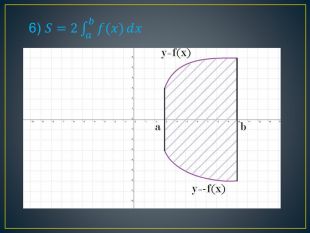
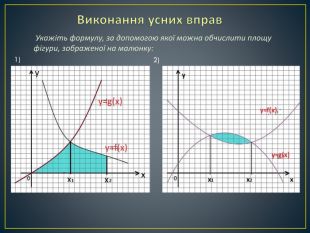
Дана презентація містить означення визначеного інтегралу, алгоритм обчислення площі криволінійної трапеції, обчисення площ різноманітних плоских фігур, оздоблений усними вправами з даної теми.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Гарна
-
-
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




![Формула Ньютона-Лейбніца. Якщо f(x) визначена і неперервна на відрізку [a;b] , а F(x) її довільна первісна на цьому відрізку(F`(x)=f(x)) то :- формула Ньютона-Лейбніца Приклад: Формула Ньютона-Лейбніца. Якщо f(x) визначена і неперервна на відрізку [a;b] , а F(x) її довільна первісна на цьому відрізку(F`(x)=f(x)) то :- формула Ньютона-Лейбніца Приклад:](/uploads/files/79014/25188/25292_images/4.jpg)
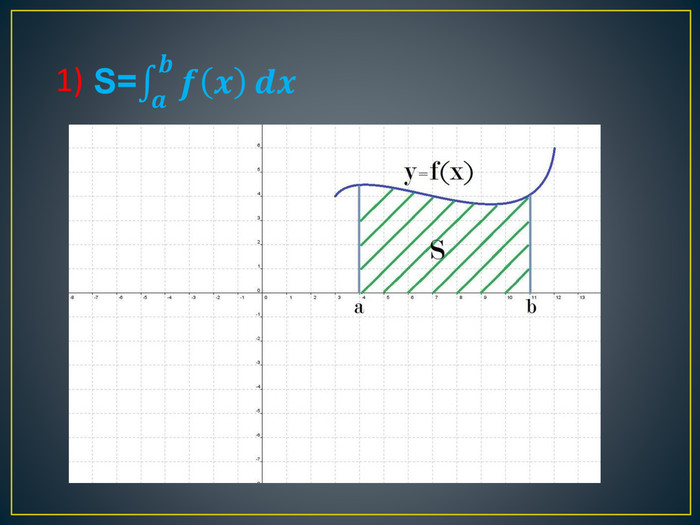
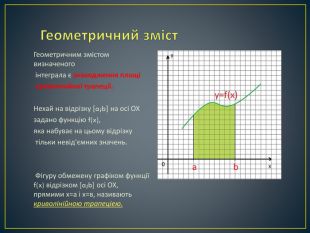
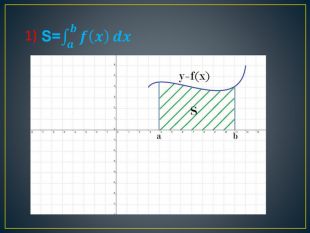
![Геометричний зміст. Геометричним змістом визначеного інтеграла є знаходження площі криволінійної трапеції. Нехай на відрізку [a;b] на осі ОХ задано функцію f(x), яка набуває на цьому відрізку тільки невід’ємних значень. Фігуру обмежену графіком функції f(x) відрізком [a;b] осі ОХ, прямими х=а і х=в, називають криволінійною трапеціею. Геометричний зміст. Геометричним змістом визначеного інтеграла є знаходження площі криволінійної трапеції. Нехай на відрізку [a;b] на осі ОХ задано функцію f(x), яка набуває на цьому відрізку тільки невід’ємних значень. Фігуру обмежену графіком функції f(x) відрізком [a;b] осі ОХ, прямими х=а і х=в, називають криволінійною трапеціею.](/uploads/files/79014/25188/25292_images/5.jpg)