Презентація з математики "Досконалість"

Досконалість в математиціВиконала:учениця 9 класу. Криворізького ліцею №123 Криворізької міської ради. Біла Тетяна

Метою роботи є: дослідження параметрів, за яких числа, многокутники будуть досконалими. Об`єктом дослідження стали числа, многокутники . Предметом дослідження – такі характеристики для чисел, як прості дільники, для фігур -площа, периметр, , які визначають досконалість фігур. Висунули гіпотезу, що із обраних типів геометричних фігур та чисел не всі можуть бути досконалими.

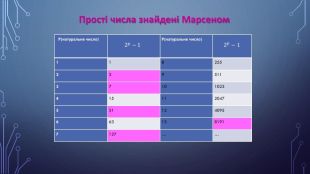
Сформулювали наступні задачі для дослідження:- ознайомитися з історією виникнення досконалих чисел та досконалих геометричних фігур;- з’ясувати зв'язок простих чисел Марсенна з досконалими числами;- дослідити параметри досконалих геометричних фігур;- обчислити радіуси вписаних кіл для знайдених досконалих геометричних фігур;- визначити радіуси описаних кіл для знайдених досконалих фігур;- встановити зв'язок досконалих чисел та досконалих геометричних фігур;- зробити висновки, узагальнення отриманих даних у вигляді таблиць для досконалих чисел та фігур. Актуальність дослідження зумовлена прагненням поглиблювати знання про геометричний світ через дослідження історії виникнення чисел, фігур.

Досконалі числа – це такі натуральні числа, в яких сума дільників, строго менших самого числа дорівнює цьому числу, наприклад: 6, 28, 496, 8128, 33550336, 85899869056…

Евклід Теорема Евкліда : «Число, 𝟐𝒑−𝟏⋅𝟐𝒑−𝟏  парне і досконале, якщо число 𝟐𝒑−𝟏 просте.»  

Марен Марсенн1588-1648 Першим винайшов прості числа за формулою 𝟐𝒑−𝟏. 

Нікомах ГераськийІІ ст. до н.е. Знайшов перші чотири досконалі числа для показника степеня р=2 ,3,5,7. Цими числами були 6, 28, 496, 8128.

Йоганн Мюллер. Винайшов в 15 ст. досконале число 33550336, при p=13.

Йоганн–Ефраїм Шейбель 1736-1809 Винайшов досконалі числа 8589869056, 137438691322, при р=17 та р=19.

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}P(натуральне число) P(натуральне число)118255239511371010234151120475311240956631381917127……2𝑝−1 2𝑝−1 Прості числа знайдені Марсеном

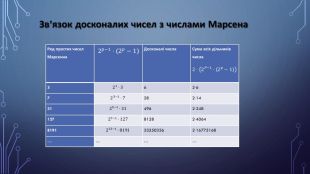
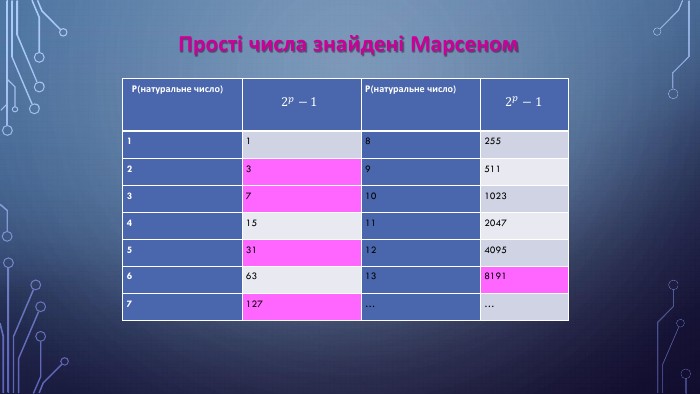
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Ряд простих чисел Марсенна 2𝑝−1⋅2𝑝−1 Досконалі числа. Сума всіх дільників числа 2⋅2𝑃−1⋅2𝑝−1321⋅362⋅6723−1⋅7282⋅143125−1⋅314962⋅24812727−1⋅12781282⋅40648191213−1⋅8191335503362⋅16775168…………{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Ряд простих чисел Марсенна. Досконалі числа36728314961278128819133550336…………Зв’язок досконалих чисел з числами Марсена

Покажемо цей зв’язок на прикладі досконалого числа 496. 496=1+2+4+8+16+31+62+124+248. 496= 1+2+4+8+16+31(1+2+4+8+16)=(1+2+4+8+16)(1+31)= 32*31=992 Це і є подвоєний добуток 496*2.

Досконалими можуть бути не тільки числа, а й фігури. До таких прийнято відносити многокутники , які володіють наступними ознаками: 1) всі їх сторони – цілі числа,2) їх площа дорівнює периметру.

За допомогою умови досконалості та формули S = pr,(a + b + c) = ½(a + b + c)*r, 1=½r,r=2. Таким чином, досконалими є ті і тільки ті трикутники, які:- описані навколо кола радіуса 2;- довжини їх сторін виражаються цілими числами.

1. Квадрат: a=4. Sкв.=16 (кв.од.), Ркв.=16(од.)2. Прямокутник: a=3, b=6 S1=6*3=18 (од.кв.), P1=2*(6+3)=18 (од.) Теорема Евкліда дала поштовх до знаходження досконалих фігур. Першими знайшли досконалі фігури піфагорійці,Досконалі чотирикутнки

Досконалі чотирикутники3. Серед паралелограмів нескінченна кількість4. Досконалі прямокутні трапеціїа=3, в=6, с=45. Досконалі рівнобедрені трапеціїа=6, в=4, с=3а=2, в=8, с=4 а=6,в=14,с=3.

ABCMLKOkkllmm222 A`B`C`M`L`K`O`k`k`l`l`m`m`444 Знаходження досконалих трикутників|AM| = |AK| = l; |MB| = |BL| = k; |LC| = |KC| = m. З рівностей k + m = a; l + m = b; k + l = c ΔA'B'C`подібний ΔABC з коефіцієнтом 2 В ньому вписане коло r = 4, і його площа більша периметра в 2 рази.

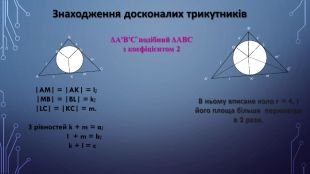
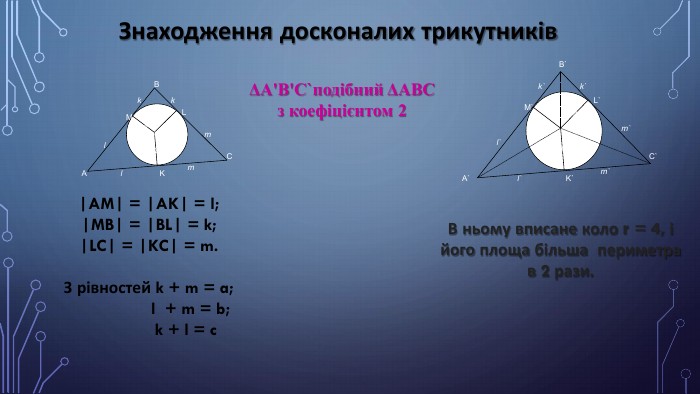
Після перетворень отримали формулу klm/4 = k + l + mk=4 С=(k + l) = 4 + 6 =10, в= (m + l) = 2 + 6 = 8, а=(k + m) = 4 + 2 = 6. Трикутник зі сторонами (10, 8, 6) Р=10+8+6=24(см) , S=Р*r=12*2=24(кв.cм) .k=8 С=(k + l) = 8 + 9 = 17, в= (m + l) = 1 + 9 = 10, а=k + m) = 8 + 1 = 9.є трикутник (17, 10, 9) P= 17+10+9=36(од.) S=18*2=36.(кв.од.)k=12 В даній рівності не існує натуральних розв’язків l і m.

k=20 Знову рівняння немає розв’язків в натуральних числах.k=16 Підставляючи натуральні значення l не знайшли натуральних значень m.k=24 a=k+m=24 +5=29 b=m=l=5+1=6 c=k+l=24+1=25. (29,6,25) Р=29+6+25=60(од.), S=3*2=60(кв.од.)

Нехай числа l і m будуть кратні 2 ,тоді формула (1) прийме вид: (q - 1)(k - 2) = 4. З неї ми знайшли досконалі трикутники зі сторонами 13 ,12, 5. S= 15*2=30 (кв.од.) , P=13+12+5=30 (од.). Нехай p = 3. Тоді (3q - 1)(3k - 2) = 20. Отримуємо трикутник зі сторонами (7, 20, 15). P =7+20+15=42 (од.), S=21*2=42 (кв.од.)

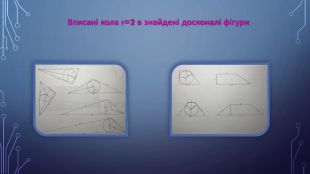
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Геометрична фігура. Параметри. Площа Периметр. Квадратa=41616 Прямокутникa=3 b=61818 Трикутники -прямокутні  -довільні a=6, b=8, c=10a=5, b=12, c=13 a=9,b=10, c=17a=6, b=25, c=29a=15, b=20, c=7 2430 366042 2430 366042 Трапеція -прямокутна -рівнобедрена a=3, b=6, h=4a=6, b=10, h=3a=6, b=8,h=4a=6 b=14 h=3 36242030 36242030 Параметри досконалих многокутників

Коло описане навколо досконалих фігур. Перевіримо цю умову для досконалих знайдених трикутників. Умова досконалості : P∆=S∆. Р∆ = a+b+c , S∆=𝐚𝐛𝐜𝟒𝐑, де R- радіус описаного кола𝒂𝒃𝒄𝟒𝑹= а+b+c𝑹=𝒂𝒃𝒄𝟒𝒂+𝒃+𝒄Встановили, що вони є різними раціональними числами. 

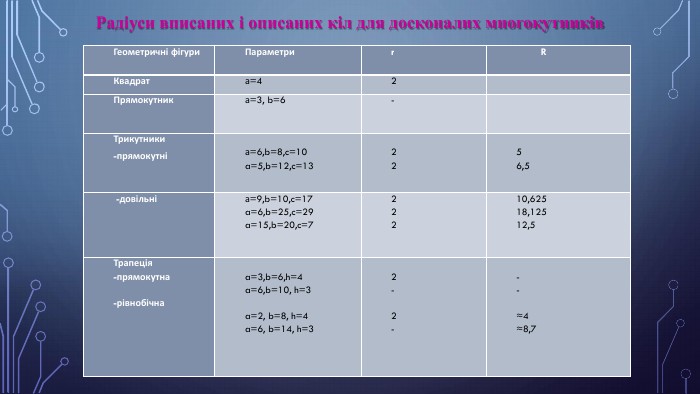
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Геометричні фігури. Параметриr RКвадрата=42 Прямокутник а=3, b=6-Трикутники-прямокутні а=6,b=8,c=10a=5,b=12,c=13 22 56,5 -довільні а=9,b=10,c=17a=6,b=25,c=29a=15,b=20,c=7  22210,62518,12512,5 Трапеція-прямокутна -рівнобічна a=3,b=6,h=4a=6,b=10, h=3 a=2, b=8, h=4a=6, b=14, h=3 2- 2- -- ≈4≈8,7 Радіуси вписаних і описаних кіл для досконалих многокутників

Вписані кола r=2 в знайдені досконалі фігури

Зв’язок досконалих чисел з многокутниками та многогранниками4 сторони + 2 діагоналі =6 досконале число12 ребер, 12 діагоналей граней і 4 діагоналі куба. Вершини з’єднані шістьма ребрами 8 сторін + 20 діагоналей = 28 – досконале число. 7 ребер, 7 сторін , а біля основи 14 діагоналей

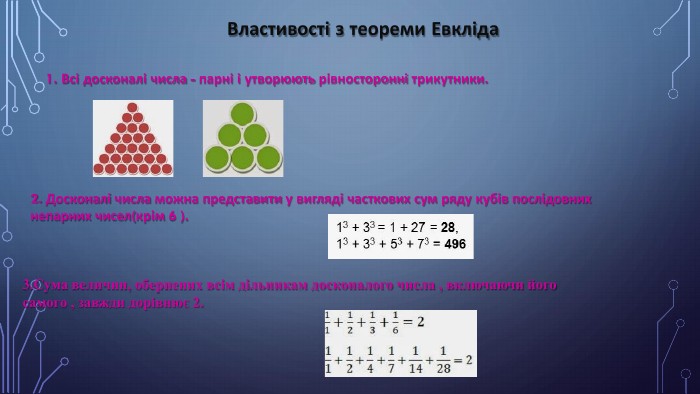
1. Всі досконалі числа - парні і утворюють рівносторонні трикутники. Властивості з теореми Евкліда2. Досконалі числа можна представити у вигляді часткових сум ряду кубів послідовних непарних чисел(крім 6 ).3. Сума величин, обернених всім дільникам досконалого числа , включаючи його самого , завжди дорівнює 2.

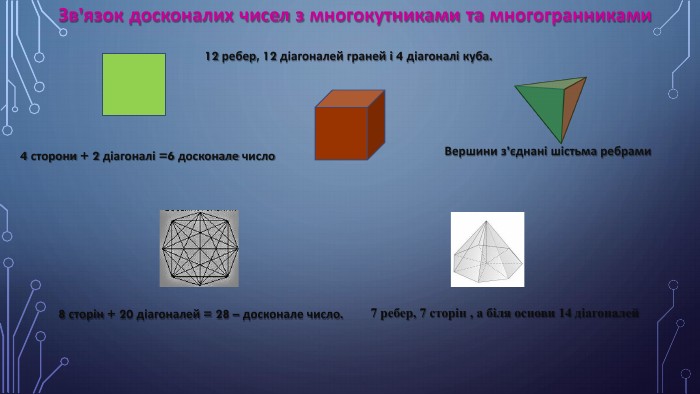
В результаті дослідження істинність гіпотези підтвердилась, що не всі числа і обрані типи геометричних фігур можуть бути досконалими. Вивчивши наукову літературу, ми прийшли до висновку , що з давніх давен вчених цікавили досконалі числа і фігури, і вони були знайдені ще Евклідом. Завдяки цій роботі з’ясували зв’язок простих чисел Марсенна з досконалими числами. Виконуючи практичну роботу дослідили і знайшли сторони досконалих фігур: трикутників, квадрата, прямокутників, трапецій та перевірили умову досконалості в них. Довели, що радіуси вписаних кіл для знайдених досконалих фігур дорівнює 2 (крім трапеції зі сторонами а=6, b=10, h=3, то а=6, b=14, h=3, та куба зі стороною а=6)Впевнились, що радіуси описаних кіл для цих фігур не є константою та не є цілими числами. Знайденні досконалі фігури закріплюють отриманні знання з шкільного курсу геометрії і можуть використовуватися для практичних робіт. З’ясували, що досконалі числа мають зв’язок з многокутниками. Триває розвиток цивілізації, зроблено безліч відкритті, але відкриття зроблені вченими і сьогодні актуальні.

Дякуємо за увагу!