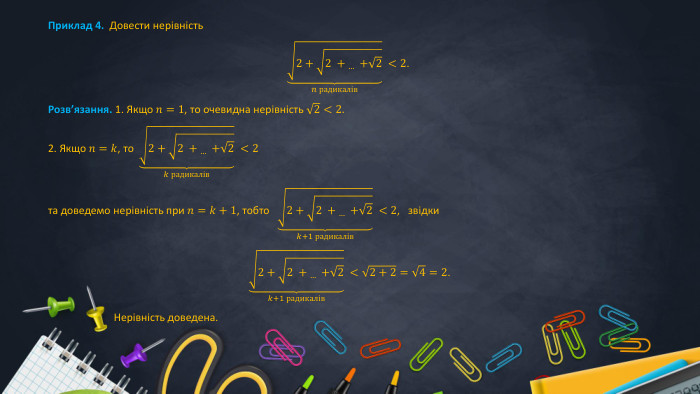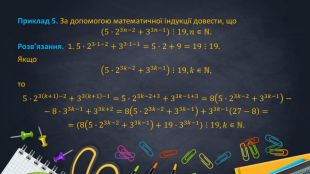Презентація за темою "Метод математичної індукції"

Метод математичної індукціїВиконала: вчитель математики Білюк К. А.

Мета Формувати в учнів навики застосування методу математичної індукції для доведення багатьох тотожностей та нерівностей, задач на подільність, теорем та властивостей, як з алгебри, так і геометрії. Розвивати логічне мислення, культуру математичного мовлення та креативність. Виховувати наполегливість, свідоме ставлення до навчання, пізнавальні інтереси учнів.

Принцип методу математичної індукції Якщо твердження 𝐴(𝑛) виконується для найменшого значення 𝑛=𝑚, для якого воно має зміст і, з припущення, що це твердження істинне для довільного натурального числа 𝑛=𝑘, випливає його істинність і для наступного числа 𝑛=𝑘+1, то твердження А(𝑛) істинне при кожному натуральному значенню 𝑛 ≥ 𝑚. Зауваження. Значенням  𝑚 не обов’язково є одиниця, так, наприклад, твердження про загальні властивості 𝑛−кутників має зміст при 𝑚 ≥ 3. 

Очевидно, що обидві частини міркування є важливими. Якщо із припущення істинності твердження 𝐴(𝑛) для деякого числа 𝑛, випливає, що воно виконується і для числа 𝑛 + 1, то це ще саме по собі нічого не дає, бо може так трапитись, що це припущення не виконується для жодного цілого значення 𝑛. Наприклад, якщо припустити, що деяке ціле число 𝑛 рівне наступному за ним, тобто що 𝑛 = 𝑛 + 1, то додавши до обох частин по одиниці, ми одержимо, що 𝑛 + 1 = 𝑛 + 2, тобто що і число 𝑛 + 1 рівне наступному за ним. Звідси зовсім не випливає, що твердження виконується для всіх 𝑛 – воно не виконується для жодного цілого числа. 

Але застосування даної схеми не є обов'язковою при використанні методу математичної індукції. При застосуванні методу математичної індукції часто дотримуються такої схеми: Перевірка, що твердження виконується для найменшого значення 𝑛, для якого воно має зміст.  Доведення, що якщо це твердження правильне для деякого натурального числа 𝑛, то воно виконується і для наступного числа 𝑛+1. 1 крок2 крок

Деколи з припущення, що твердження виконується для двох послідовних чисел 𝑛 − 1 і 𝑛, доводиться, що воно виконується для числа 𝑛 + 1. В цьому випадку у якості першого кроку міркувань необхідно перевірити, що припущення виконується для двох перших значень 𝑛, наприклад, для 𝑛 = 1 і 𝑛 = 2. Іноді в якості другого кроку міркувань доводять справедливість припущення для деякого значення 𝑛, припускаючи його прaвильність для всіх натуральних 𝑘, менших 𝑛. 

Приклади. Приклад 1. Обчислити суму 𝑛 перших непарних чисел1 + 3 + 5 + ... + (2𝑛 − 1). Розв’язання. Нехай 𝑆𝑛=1 + 3 + 5 + ... + (2𝑛 − 1). Підставимо послідовно 𝑛 = 1, 2, 3, 4, 5, тоді:𝑆(1) = 1,𝑆(2) = 1 + 3 = 4,𝑆(3) = 1 + 3 + 5 = 9, 𝑆(4) = 1 + 3 + 5 + 7 = 16, 𝑆(5) = 1 + 3 + 5 + 7 + 9 = 25. 

Зауважимо, що при 𝑛=1, 2, 3, 4, 5 сума 𝑛 послідовних чисел дорівнює 𝑛2. Припустимо, що для деякого числа 𝑛, формула 𝑆𝑛=𝑛2справедлива, і будемо намагатися довести, що тоді вона справедлива і для наступного числа 𝑛+1. Таким чином, припускаємо, що 𝑆𝑛=1+3+5+...+2𝑛−1=𝑛2,обчислимо𝑆𝑛+1=𝑛2+2𝑛+1=(𝑛+1)2. Отже, з припущення, що формула 𝑆𝑛=𝑛2 виконується для деякого нату-рального числа 𝑛 довели її правильність і для наступного числа𝑛+1. Формула буде правильна і для числа 𝑛=6 , яке наступне після 5, а тоді правильна і для 𝑛=7, і для 𝑛=8, і для 𝑛=9, тощо. Тепер формула може рахуватись доведенням для будь-якого числа доданків. Цей метод доведення називається методом математичної індукції.  

Метод математичної індукції, по своїй суті пов’язаний з поняттям числа, тому, природньо, має найбільше застосування у арифметиці, в алгебрі та теорії чисел. Розглянемо декілька прикладів застосування методу математичної індукції. Приклад 2. Довести, що 1∙1!+2∙2! + …+ 𝑛∙𝑛!=𝑛+1!−1. Розв’язання. 1. Якщо n = 1, то твердження істинне.2. Припустимо істинність твердження при 𝑛=𝑘, тобто 1∙1!+2∙2! + …+𝑘∙𝑘!=𝑘+1!−1,доведемо істинність при 𝑛=𝑘+1:1∙1!+2∙2!+ …+𝑘∙𝑘!+𝑘+1∙𝑘+1!=𝑘+2!−1. Ліва чaстина рівності дорівнює: 1∙1!+2∙2!+ …+𝑘∙𝑘!+𝑘+1∙𝑘+1!=𝑘+1!−1+𝑘+1∙𝑘+1!==𝑘+1!∙1+𝑘+1−1=𝑘+1!∙𝑘+2−1=𝑘+2!−1. Твердження доведено. 

Приклад 3. Довести тотожність для довільного натурального числа 𝑛.13+23 + 33+...+ 𝑛3=𝑛(𝑛+1)22. Розв’язання. 1. При 𝑛=1: 13=1=1(1+1)22 Припускаємо істинність твердження при 𝑛=𝑘: 13+23 + 33+...+ 𝑘3=𝑘(𝑘+1)22,то13+23 + 33+…+𝑘+13=13+23 + 33+…+ 𝑘3+𝑘+13==𝑘(𝑘+1)22+𝑘+13=𝑘+122𝑘2+4𝑘+4=𝑘+1𝑘+222.  Тотожність доведена.  

Приклад 4. Довести нерівність2+2 + … +2𝑛 радикалів <2. Розв’язання. 1. Якщо 𝑛=1, то очевидна нерівність 2<2.2. Якщо 𝑛=𝑘, то 2+2 + … +2𝑘 радикалів <2та доведемо нерівність при 𝑛=𝑘+1, тобто 2+2 + … +2𝑘+1 радикалів <2, звідки 2+2 + … +2𝑘+1 радикалів <2+2=4=2. Нерівність доведена. 

Приклад 5. За допомогою математичної індукції довести, що 5∙23𝑛−2+33𝑛−1⋮19, 𝑛∊ℕ. Розв’язання. 1. 5∙23∙1−2+33∙1−1=5∙2+9=19⋮19. Якщо 5∙23𝑘−2+33𝑘−1⋮19, 𝑘∊ℕ,то 5∙23𝑘+1−2+33𝑘+1−1=5∙23𝑘−2+3+33𝑘−1+3=85∙23𝑘−2+33𝑘−1−− 8∙33𝑘−1+33𝑘+2=85∙23𝑘−2+33𝑘−1+33𝑘−127−8==(85∙23𝑘−2+33𝑘−1+19∙33𝑘−1)⋮19, 𝑘∊ℕ. 

Приклад 6. Довести, що для довільного 𝑛∊ℕ число(11𝑛+1+122𝑛−1)⋮133. Розв’язання. 1. 111+1+122∙1−1=121+12=133⋮133. Якщо (11𝑘+1+122𝑘−1)⋮133, то(11𝑘+1+1+122𝑘+1−1=11(11𝑘+1+122𝑘−1)−11∙122𝑘−1+122𝑘+2==11(11𝑘+1+122𝑘−1)+122𝑘−1122−11==(11(11𝑘+1+122𝑘−1)+122𝑘−1∙133)⋮133. Твердження доведено. 

Висновок Метод математичної індукції грає провідну роль в процесі доведення багатьох тотожностей та нерівностей, задач на подільність, теорем та властивостей, як з алгебри, так і геометрії та інших розділів математики. Цей метод призначений для того, щоб довести або спростувати деякі гіпотези, отримані за допомогою неповної індукції, що можуть виявитись хибними.

Дякую за увагу!