Презентація "Задачі на рух"
Про матеріал
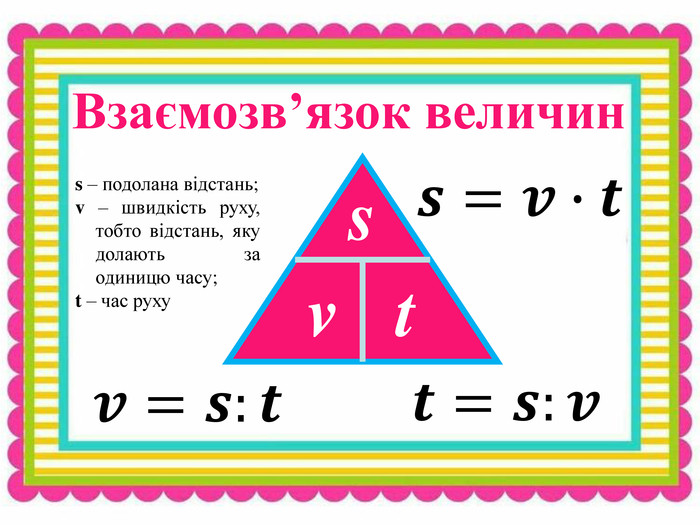
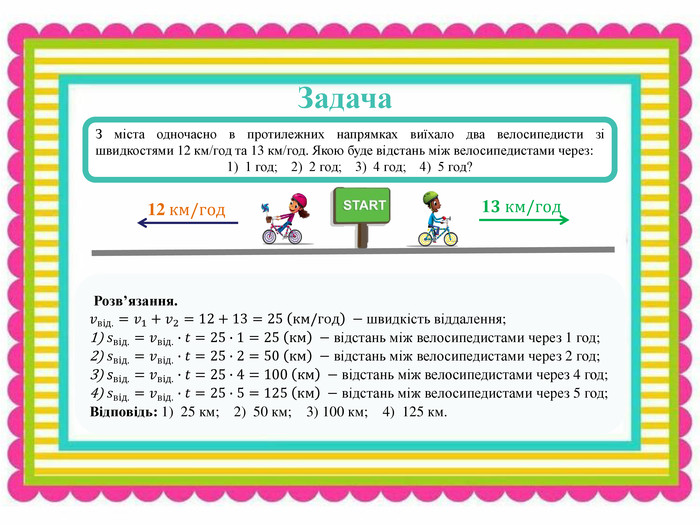
Сформувати вміння учнів розв'язувати задачі практичного змісту, зокрема на рух, використовуючі формули відстані, швидкості, часу. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Щиро дякую!!!


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку