Презентація "Задачі на суміші і сплави"
Про матеріал
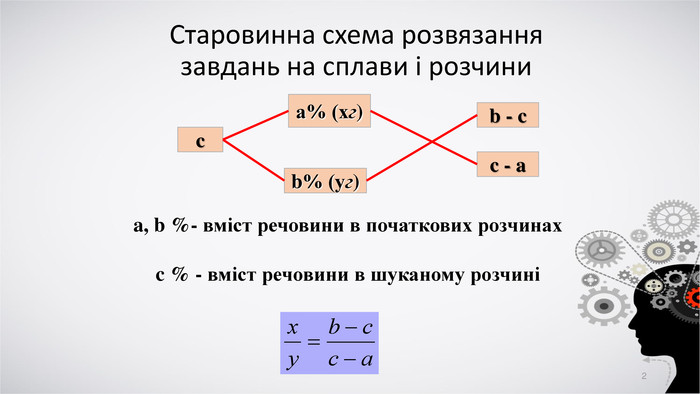
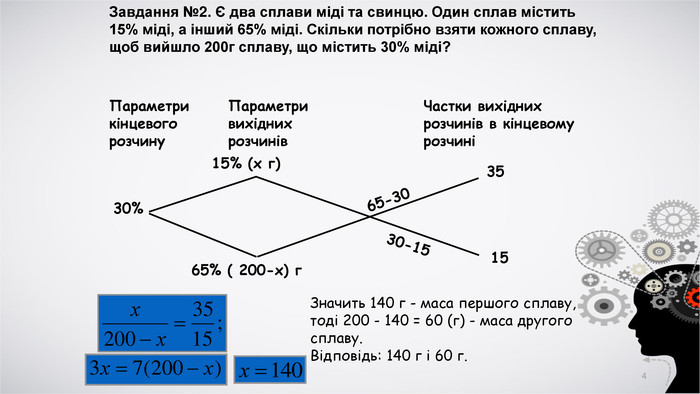
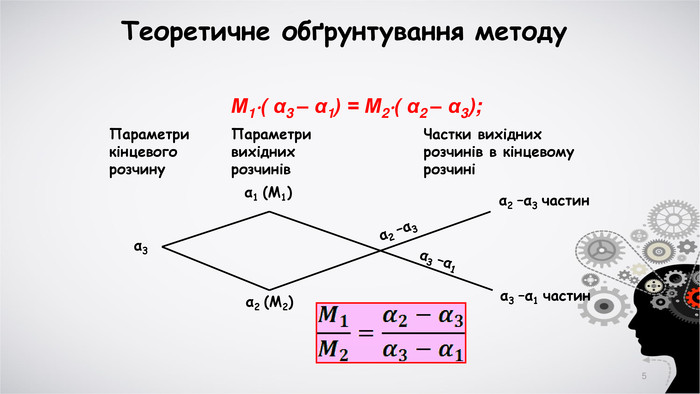
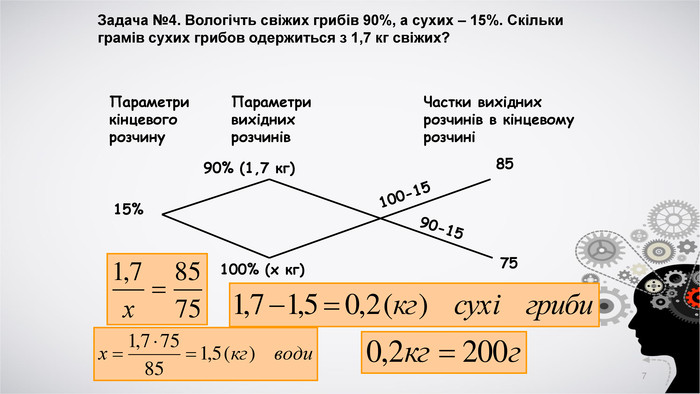
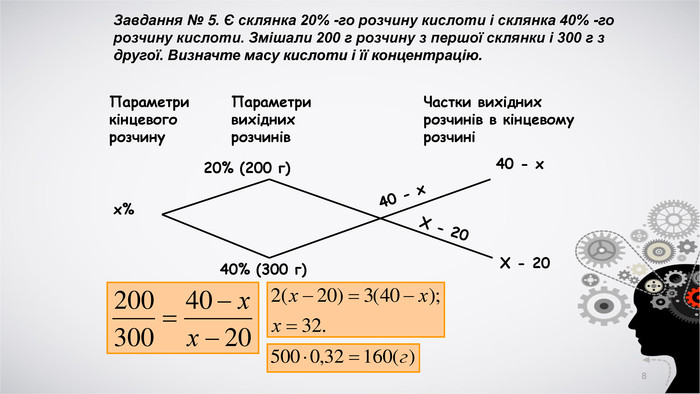
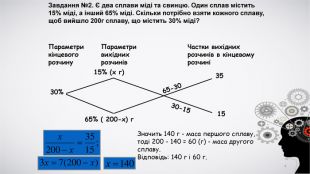
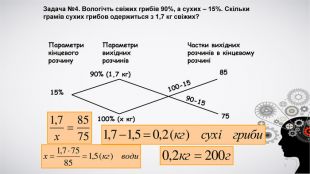
В презентації надається старовинна схема розв'язання завдань на сплави і розчини, а також теоретичне обґрунтування методу.
Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку