Роз'яснення теми "Модуль в математиці"для учнів 6-10 класів.
Тема: «Модуль в математиці»
Означення і основні властивості модуля
Абсолютним значенням числа ![]() (позначається
(позначається ![]() ) називається відстань від точки. Яка зображує дане число
) називається відстань від точки. Яка зображує дане число ![]() на координатній прямій, до початку відліку. З означення випливає, що
на координатній прямій, до початку відліку. З означення випливає, що 
Властивості:
1) ![]() 7)
7) ![]()
![]()
![]()
2) ![]() 8)
8) ![]()
![]()
![]() і
і ![]()
3) ![]() 9)
9) ![]()
![]()
![]()
4) ![]() 10)
10) ![]()
![]()
![]()
5) 5) 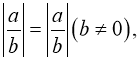 11)
11) 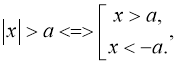
6) ![]() 12)
12) 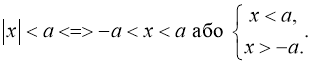
Завдання для 6 класу
Модуль числа
1. а) Знайти число ![]() , якщо
, якщо ![]()
![]()
![]()
б) Розв’язати рівняння ![]()
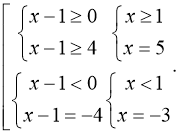 Відповідь: -3;5.
Відповідь: -3;5.
За означенням модуля ![]() або
або ![]()
![]() або
або ![]()
Перевірка ![]()
![]()
Прямокутна система координат
2. а) Де на координатній площині лежать точки, координати яких задовольняють умову:
*) ![]() і
і ![]() **)
**) ![]() і
і ![]() ***)
***) ![]() і
і ![]()
Розв’язання: (мал. 1).
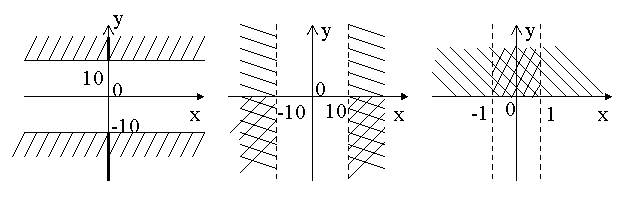
![]()

Додавання і віднімання раціональних чисел
3. а) Виконати дії
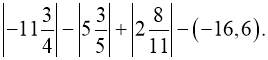
Розв’язання:
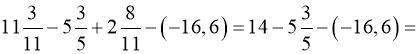
![]()
б) Розв’язати рівняння і зробити перевірку ![]()
Розв’язання: ![]()
![]()
![]()
Ділення і множення раціональних чисел
4. а) Обчислити ![]()
![]() якщо
якщо ![]()
![]()
![]()
![]()
![]()
![]()
Розв’язання: ![]()
![]()
![]()
![]()
![]()
Два інших – аналогічно.
б) При яких натуральних значеннях ![]() справджується нерівність
справджується нерівність
![]()
![]()
![]()
![]() при всіх
при всіх ![]()
![]()
![]()
![]() при
при ![]()
![]()
Завдання для 7 класу
Вирази зі змінами
1. а) Записати вираз без знака модуля ![]()
![]()
![]()
Розв’язання: За означенням модуля маємо:
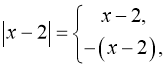
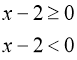 або
або 
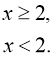
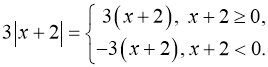
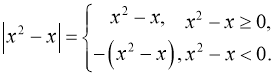
б) При яких значеннях ![]() правильна рівність?
правильна рівність?
![]() при
при ![]()
![]() при
при ![]()
![]()
![]() при
при ![]()
Лінійні рівняння з однією змінною
2. а) Чи мають коріння рівняння?
![]() – так,
– так, ![]() – так,
– так, ![]() – ні,
– ні, ![]() – так,
– так, ![]() – так,
– так, ![]() – так.
– так.
б) Чи рівносильні рівняння?
![]() і
і ![]() – так.
– так.
![]() і
і ![]() – так.
– так.
![]() і
і ![]() – ні.
– ні.
в) Яке з рівнянь рівносильне рівнянню ![]() : а)
: а) ![]() (Вірно), б)
(Вірно), б) 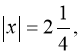 в)
в) ![]()
Лінійна функція та її графік
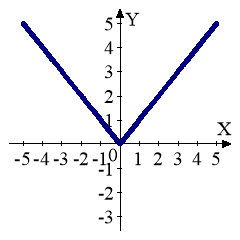 3. Побудувати графік функції:
3. Побудувати графік функції:
![]()
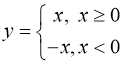 (Мал. 2).
(Мал. 2).
![]()
![]()
![]()
![]() 1)
1) 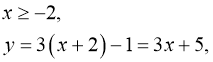
2) 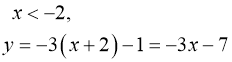 (мал. 3).
(мал. 3).
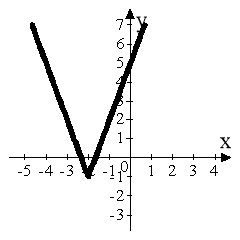
Завдання для 8 класу
Розв’язування квадратних рівнянь
1. Розв’язати рівняння ![]()
![]() I спосіб:
I спосіб:
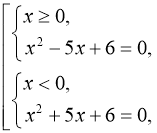
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Відповідь: –2; –3; 2; 3.
Відповідь: –2; –3; 2; 3.
II спосіб:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Відповідь: –3; –2; 2; 3.
Відповідь: –3; –2; 2; 3.
Розв’язування лінійних нерівностей з однією змінною
2. ![]()
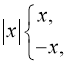
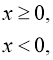
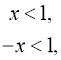
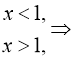
![]()
![]() Або за властивістю модуля:
Або за властивістю модуля: 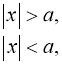 тоді
тоді ![]()
![]()
![]()
![]()
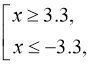
![]()
![]()
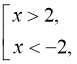
![]()
Розв’язування систем нерівностей з однією змінною
3. 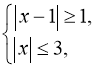
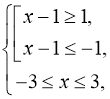
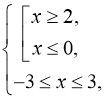
![]() (мал. 4).
(мал. 4).
![]()
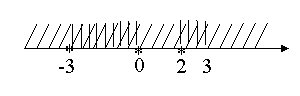 Завдання для 9 класу
Завдання для 9 класу
Функція та її властивості
1. Розглянути графік і властивості функції ![]()
![]()
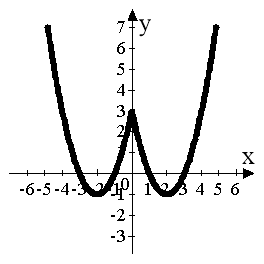
Побудова графіка квадратичної функції
2. Побудувати графік функції ![]()
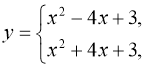
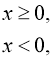 (мал. 5).
(мал. 5).
Розв’язування лінійних рівнянь та нерівностей, що містять модуль
3. а) Розв’язати рівняння ![]() б) Розв’язати нерівність
б) Розв’язати нерівність ![]()
![]()
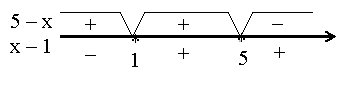 Розв’язання: а)
Розв’язання: а) ![]()
![]()
![]() (мал. 6)
(мал. 6)
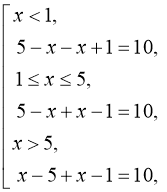
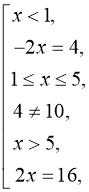
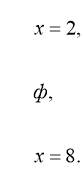 Відповідь: –2; 8.
Відповідь: –2; 8.
![]()
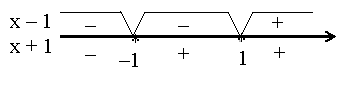 б)
б) ![]()
![]()
![]() (мал. 7).
(мал. 7).
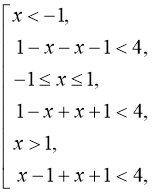
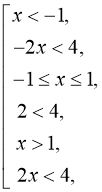
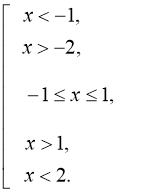
Відповідь: ![]()
Побудуємо графіки функцій ![]()
![]()
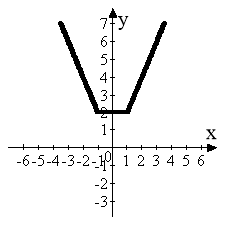
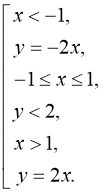
![]() (мал. 8).
(мал. 8).
![]() Розв’язування нерівностей другого ступеня з однією змінною
Розв’язування нерівностей другого ступеня з однією змінною
4. На основі властивості модуля 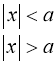 а)
а) ![]()
б) ![]() в) На основі означення модуля
в) На основі означення модуля ![]()
Розв’язування:
а) 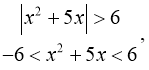
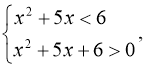
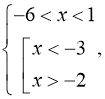 (мал. 9).
(мал. 9).
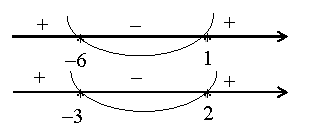
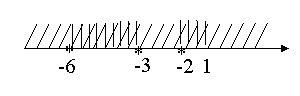
![]()
б) ![]()
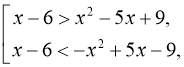
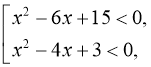
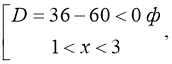
![]()
в) ![]()
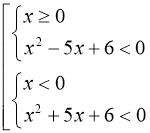
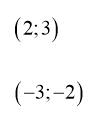
![]()
Розв’язування рівнянь, що зводяться до квадратних
1. Розв’язати рівняння: ![]()
Розв’язання:
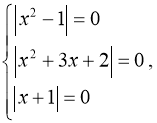
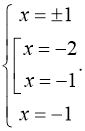 Відповідь:
Відповідь: ![]() .
.
2. Розв’язати рівняння: ![]()
Розв’язання: заміна ![]() тоді
тоді ![]()
![]()
![]()
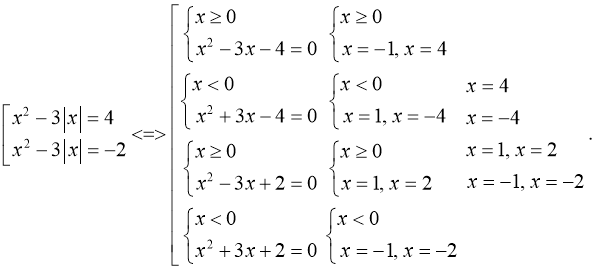
Відповідь: –4; –2; –1; 1; 2; 4.
Завдання 10 клас
Співвідношення між тригонометричними функціями
1. Довести тотожність 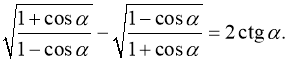
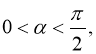
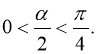
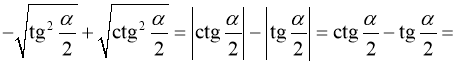
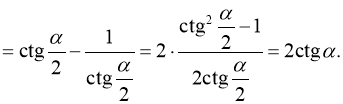 Доведено.
Доведено.
Тригонометричні рівняння і нерівності
1. Розв’язати рівняння: а) ![]() б)
б) 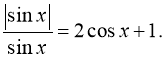
Розв’язання:
а) Оскільки ![]()
![]() то рівняння рівносильне системі:
то рівняння рівносильне системі:
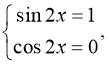
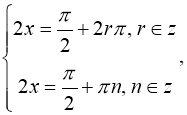
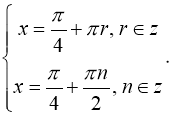
Відповідь: 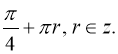
б) 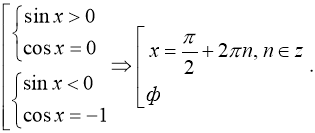
Відповідь: 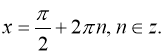
Ірраціональні показникові тригонометричні рівняння і нерівності
1. Розв’язати рівняння:
а)![]() б)
б) ![]()
в) 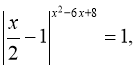 г)
г) 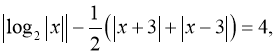
д) 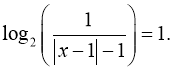
Розв’язання:
а) ![]()
![]()
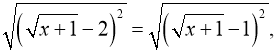
![]() Розглянемо три випадки:
Розглянемо три випадки:
1: ![]() коренів немає.
коренів немає.
2: ![]()
3: ![]() коренів немає.
коренів немає.
Другий випадок: ![]()
![]()
![]()
![]() Відповідь: 1,25.
Відповідь: 1,25.
б) ![]()
в) 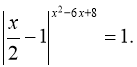 Розглянемо два випадки:
Розглянемо два випадки:
1) 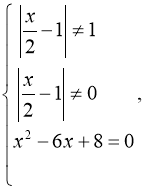
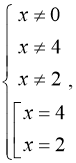
![]()
2) 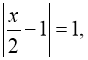
![]() Оскільки
Оскільки ![]() для будь-якого
для будь-якого ![]() то ці значення є коренями рівняння. Відповідь: 0; 4.
то ці значення є коренями рівняння. Відповідь: 0; 4.
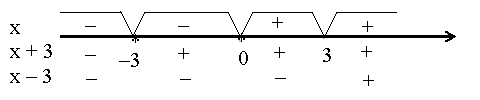 г)
г) 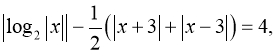 (мал. 10).
(мал. 10).
![]()
1) 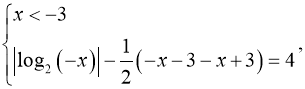
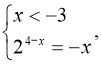
![]()
2) 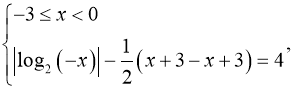
![]()
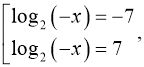
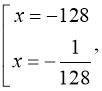
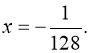
3) 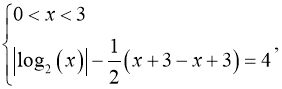
![]()
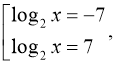
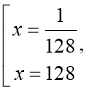
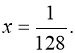
4) 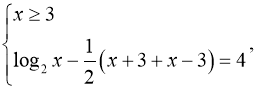
![]()
![]()
![]() Відповідь:
Відповідь: 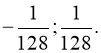
д) ![]()
![]()
2. Розв’язати нерівності:
а) ![]() б)
б) ![]() в)
в) 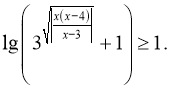
г) 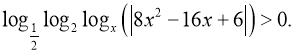
Розв’язання:
а) ![]()
![]()
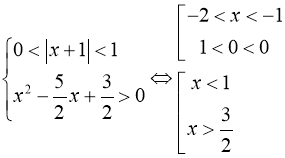 в цьому випадку
в цьому випадку ![]()
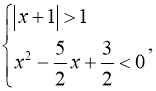
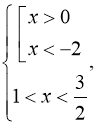

Відповідь: ![]()
б) 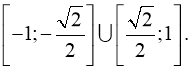
в) 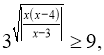
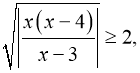
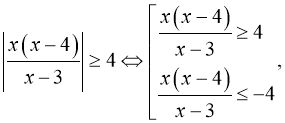
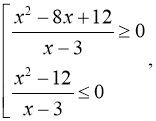
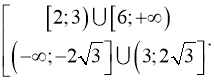
Відповідь: ![]()
г) 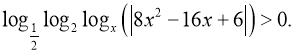
ОДЗ: 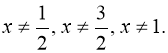
![]()
![]()
![]()
Якщо 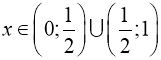 маємо систему.
маємо систему. 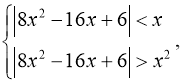
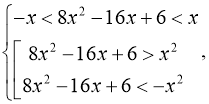
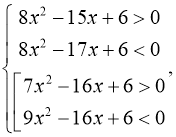
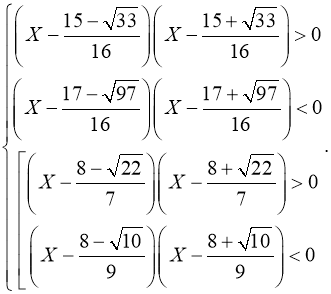
Відповідь: 
Завдання 11 клас
12. Розв’язати рівняння:
а) ![]()
б) ![]()
в) ![]()
Розв’язання рівнянь та нерівностей, що містять знак модуля
1. Розв’язання рівнянь виду ![]()
Оскільки ![]() якщо
якщо ![]() то
то ![]()
Приклад 1. Розв’язати рівняння ![]()
Розв’язання. Маємо ![]() або
або ![]() Корінь першого рівняння
Корінь першого рівняння ![]() а другого
а другого ![]() Отже,
Отже, ![]()
Приклад 2. Розв’язати рівняння 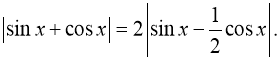
Розв’язання. Дане рівняння розпадається на два: ![]()
![]() Розв’язання першого рівняння
Розв’язання першого рівняння ![]() а другого
а другого ![]() Відповідь:
Відповідь: ![]() і
і ![]()
Вправи
Розв’язати рівняння:
1. 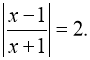 4.
4. ![]()
2. ![]() 5.
5. ![]()
3. 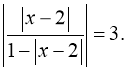 6.
6. ![]()
2. Розв’язання рівнянь виду ![]()
Вкажемо два прийоми розв’язання цих рівнянь.
1. Рівняння ![]() має корні, коли
має корні, коли ![]() Отже,
Отже, 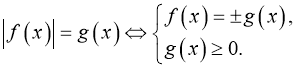 Тому достатньо розв’язати два рівняння
Тому достатньо розв’язати два рівняння ![]()
![]() і для знайдених значень
і для знайдених значень ![]() перевірити справедливість нерівності
перевірити справедливість нерівності ![]()
2. Оскільки ![]() якщо
якщо ![]() і
і ![]() якщо
якщо ![]() то рівняння
то рівняння ![]() рівносильне кожній із наступних систем:
рівносильне кожній із наступних систем: 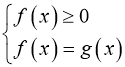 або
або 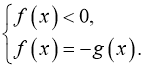 У першій системі, розв’язав рівняння
У першій системі, розв’язав рівняння ![]() для знайдених коренів треба перевірити виконання умови
для знайдених коренів треба перевірити виконання умови ![]() Аналогічні міркування приводять і для другої системи.
Аналогічні міркування приводять і для другої системи.
Зауваження. Можна розв’язати рівняння ![]() і
і ![]() і корні кожного з них перевірити підстановкою в рівняння
і корні кожного з них перевірити підстановкою в рівняння ![]() .
.
Приклад 3. Розв’язати рівняння ![]()
Розв’язання. Тут скористаймося першим прийомом. Розв’яжемо рівняння ![]() і
і ![]() Перше з них має корні –2/3 і 0, а друге 0 і –3/2. Легко побачити, що умова
Перше з них має корні –2/3 і 0, а друге 0 і –3/2. Легко побачити, що умова ![]() виконується лише при
виконується лише при ![]() і при
і при ![]() Отже, –2/3 і 0 – корні первинного рівняння.
Отже, –2/3 і 0 – корні первинного рівняння.
1


про публікацію авторської розробки
Додати розробку
