Презентація на тему ознаки подільності натуральних чисел

ОЗНАКИ ПОДІЛЬНОСТІ НАТУРАЛЬНИХ ЧИСЕЛ27.10.2021

УРОК 1

ОЗНАКА ПОДІЛЬНОСТІ на 2, на 5 і на 10

Ознаки подільності на 2 Число ділиться на 2 тоді і тільки тоді, коли його остання цифра ділиться на 2, тобто є парною. Наприклад:2, 8, 16, 24, 66, 150 — діляться на 2, так як остання цифра цих чисел парна;3, 7, 19, 35, 77, 453 — не діляться на 2, так яка остання цифра цих чисел непарна.

ПРИКЛАД 1 : Дано числа : 544,857,145,292,598,641. Записати у перший стовпчик всі числа,які діляться на 2, а в другий стовпчик записати всі числа,які не діляться на 2. Отже , перший стовпчик-це ті числа , в яких остання цифра є парною. Тобто: 544 , 292 , 598. Отже , другий стовпчик-це ті числа , в яких остання цифра є не парною. Тобто: 857, 145 , 641. Тому : 544 857 292 145 598 641 ЗАВДАННЯ 1 : Дано числа : 358,191,445,784,396,723. Записати у перший стовпчик всі числа,які діляться на 2, а в другий стовпчик записати всі числа,які не діляться на 2.

ПРИКЛАД 2 : Дано числа 18,95,74,198,73. Знайти суму всіх чисел , які діляться на 2. Розв’язок: На 2 діляться такі числа : 18,74,198.Їхня сума : 18+74+198=290 ВІДПОВІДЬ : 290. ЗАВДАННЯ 2 : Дано числа 138,241,436,88,397. Знайти суму всіх чисел , які діляться на 2.

ПРИКЛАД 3 : Знайдіть усі значення х , які кратні числу 2 і при яких буде правильною дана нерівність 44

ПРИКЛАД 4 : Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 2.1)25* , 2)456* , 3)19*Розв’язок: Число ділиться на 2 тоді і тільки тоді, коли його остання цифра ділиться на 2, тобто є парною. Тому ми можемо замість зірочки поставити будь-які числа , які діляться на 2.1)25* Числа : 0,2,4,6,8.2)456* Числа : 0,2,4,6,8.3) 19* Числа : 0,2,4,6,8. ЗАВДАННЯ 4 : Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 2.1)144* , 2)392* , 3)28*

Ознаки подільності на 5 Число ділиться на 5 тоді, коли його остання цифра дорівнює 0 або 5. Наприклад:375, 5680, 233575 — діляться на 5, так як їх остання цифра дорівнює 0 або 5;9634, 452, 389753 — не діляться на 5, так як їх остання цифра не дорівнює 0 або 5.

ПРИКЛАД 1 : Дано числа 390,55,74,485,273. Знайти суму всіх чисел , які діляться на 5. Розв’язок: На 5 діляться такі числа : 390,55,485.Їхня сума : 390+55+485=930 ВІДПОВІДЬ : 930. ЗАВДАННЯ 1 : Дано числа 840,245,637,105,741. Знайти суму всіх чисел , які діляться на 5. ПРИКЛАД 2 : Дано числа : 445,447,591,250,680,841. Записати у перший стовпчик всі числа,які діляться на 5, а в другий стовпчик записати всі числа,які не діляться на 5. Отже , перший стовпчик-це ті числа , в яких остання цифра-це 0 або 5. Тобто: 445 , 250 , 680. Отже , другий стовпчик-це ті числа , в яких остання цифра-це всі числа,крім 0 та 5. Тобто: 447, 591 , 841. Тому : 445 447 250 591 680 841

ЗАВДАННЯ 2 : Дано числа : 355,791,522,430,895,423. Записати у перший стовпчик всі числа,які діляться на 5, а в другий стовпчик записати всі числа,які не діляться на 5. ПРИКЛАД 3 : Знайдіть усі значення х , які кратні числу 5 і при яких буде правильною дана нерівність 85

ПРИКЛАД 4 : Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 5.1)50* , 2)148* , 3)519*Розв’язок: Число ділиться на 5 тоді, коли його остання цифра дорівнює 0 або 5. Тому ми можемо замість зірочки поставити 0 або 5.1)50* Числа : 0,5.2)148* Числа : 0,5.3) 519* Числа : 0,5. ЗАВДАННЯ 4 : Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 5.1)34* , 2)168* , 3)756*

Ознаки подільності на 10 Число ділиться на 10 тоді і тільки тоді, коли воно закінчується на нуль. Наприклад:460, 24000, 1245464570 — діляться на 10, так як остання цифра цих чисел дорівнює нулю;234, 25048, 1230000003 — не діляться на 10, так як остання цифра цих чисел не дорівнює нулю.

ПРИКЛАД 1 : Дано числа 900,75,10,531,270. Знайти суму всіх чисел , які діляться на 10. Розв’язок: На 10 діляться такі числа(бо вони закінчуються нулем) : 900,10,270.Їхня сума : 900+10+270=1180 ВІДПОВІДЬ : 1180. ЗАВДАННЯ 1 : Дано числа 450,385,237,700,410. Знайти суму всіх чисел , які діляться на 10. ПРИКЛАД 2 : Знайдіть усі значення х , які кратні числу 10 і при яких буде правильною дана нерівність 90

ПРИКЛАД 3 : Дано числа : 440,447,911,500,830,641. Записати у перший стовпчик всі числа,які діляться на 10, а в другий стовпчик записати всі числа,які не діляться на 10. Отже , перший стовпчик-це ті числа , в яких остання цифра-це 0 . Тобто: 440 , 500 , 830. Отже , другий стовпчик-це ті числа , в яких остання цифра-це всі числа,крім 0. Тобто: 447, 911 , 641. Тому : 440 447 500 911 830 641 ЗАВДАННЯ 3 : Дано числа : 760,891,302,590,495,380. Записати у перший стовпчик всі числа,які діляться на 10, а в другий стовпчик записати всі числа,які не діляться на 10.

ПРИКЛАД 4 : Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 10.1)456* , 2)23* , 3)814*Розв’язок: Число ділиться на 10 тоді, коли його остання цифра дорівнює 0 . Тому ми маємо замість зірочки поставити 0 .1)456* Число 0.2)23* Число 0.3)814* Число 0. ЗАВДАННЯ 4 : Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 10.1)456* , 2)198* , 3)64*

КОНТРОЛЬНИЙ ТЕСТ1. З чисел:555,900,345,514,780,530,405,618 виписати ті , які 1)діляться на 5 ; 2)діляться на 10.2. Запишіть будь-яке чотирицифрове число , яке кратне 10.3. Запишіть значення х ,які кратні числу 2 , при яких нерівність 32<х<97 буде правильною.4. Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 5.1)120* , 2)81* , 3)919*5. З чисел:442,910,538,47,600,521,385,68 виписати ті , які діляться на 2.6. Запишіть будь-яке чотирицифрове число , яке кратне 2.7. 3. Запишіть значення х ,які кратні числу 10 , при яких нерівність 67<х<111 буде правильною.

УРОК 2

Ознаки подільності на 9 і на 3

Ознака подільності на 9: Якщо сума цифр числа ділиться націло на 9, то й саме число ділиться націло на 9. Якщо сума цифр числа не ділиться націло на 9, то й саме число не ділиться націло на 9. Ознака подільності на 3: Якщо сума цифр числа ділиться націло на 3, то й саме число ділиться націло на 3. Якщо сума цифр числа не ділиться націло на 3, то й саме число не ділиться націло на 3.

Якщо сума цифр числа ділиться націло на 9, то й саме число ділиться націло на 9: Наприклад: Число 1476 ділиться на 9, оскільки 1+4+7+6= 18, а число 18 ділиться на 9. Число 1239 не ділиться на 9, оскільки 1 + 2 + 3+ 9=15,а число 15 не ділиться на 9. Приклад 1: Запишемо ці числа 288, 361, 441, 814, 917, 8919 до першого стовпчика ті, що діляться на 9, а до другого ті, що не діляться на 9 Для цього знайдемо суми цифр кожного із цих чисел і подивимось яка з нихділиться на 9: 288: 2 + 8 + 8 = 18 361: 3 + 6 + 1 = 10 441: 4 + 4 + 1= 9 814: 8 + 1 +4 = 13 8919: 8 + 9 + 1 + 9 = 27 917: 9 + 1 + 7 = 17 Отже, 288 361 441 814 8919 917 Завдання 1: Запишіть ці числа 296, 45890, 5400, 450, 7485, 3960 до першого стовпчика ті, що діляться на 9, а до другого ті, що не діляться на 9.27.10.2021

Приклад 2: Знайдіть усі значення у, що кратні числу 9 і при яких буде правильною нерівність 90 < у < 126. Розв’язання: 90 < у < 128,На 9 діляться 99, 108, 117, 126. 99: 9 + 9 = 18,108: 1 + 0 + 8 = 9,117: 1 + 1 + 7 = 9,126: 1 + 2 + 6 = 9. Отже, у = 99, 108, 117, 126. Відповідь: у = 99, 108, 117, 126. Завдання 2: Знайдіть усі значення у, що кратні числу 9 і при яких буде правильною нерівність 40 < у < 96.27.10.2021

Приклад 3: Знайдіть усі трицифрові числа, які містять цифри 5 і 1 та діляться на 9. Розв’язання: Позначимо невідому цифру зірочкою. Сума і цифр шуканого числа дорівнює: 5 + 1 + * = 6 + *. Ця сума має ділитися на 9, тому замість зірочки можна підставити тільки цифру 3. А далі з цифр 1, 3, 5 складаємо всі можливі трицифрові : Числа: 135; 153; 315; 351; 513; 531. Завдання 3: Знайдіть усі трицифрові числа, які містять цифри 6 і 2 та діляться на 9.27.10.2021

Приклад 4: Чи можна з даних цифр скласти чотирицифрове число, що не містить однакових цифр, яке ділиться на 9:1) 3, 6, 7, 9; 2) 6, 5, 8, 8 Розв’язання: Знайдемо суму цих чисел, якщо вона ділиться на 9, то можна скласти число, що ділиться на 9:1) 3+6+7+9=25, не ділиться, значить неможна;2) 6+5+8+8=27, ділиться, значить можна. Завдання 4: Чи можна з даних цифр скласти чотирицифрове число, що не містить однакових цифр, яке ділиться на 9:1) 4, 6, 0, 9; 2) 9, 1, 2, 627.10.2021

Якщо сума цифр числа ділиться націло на 3, то й саме число ділиться націло на 3. Приклад 1: Чи ділиться число 7854 націло на 3. Розв’язання : Оскільки сума цифр числа 7854, 7 + 8 + 5 + 4 = 24, ділиться націло на 3, то і саме число ділиться на 3. Відповідь. Число 7854 ділиться націло на 3. Завдання 1: Чи число 3749 ділиться націло на 3.27.10.2021

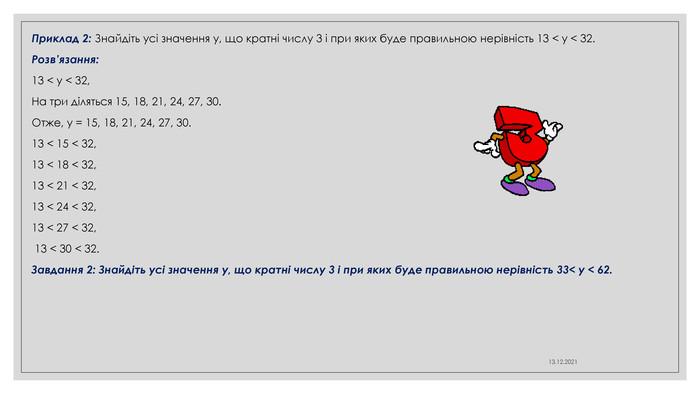
Приклад 2: Знайдіть усі значення у, що кратні числу 3 і при яких буде правильною нерівність 13 < у < 32. Розв’язання:13 < у < 32,На три діляться 15, 18, 21, 24, 27, 30. Отже, у = 15, 18, 21, 24, 27, 30.13 < 15 < 32,13 < 18 < 32,13 < 21 < 32,13 < 24 < 32,13 < 27 < 32, 13 < 30 < 32. Завдання 2: Знайдіть усі значення у, що кратні числу 3 і при яких буде правильною нерівність 33< у < 62.27.10.2021

Приклад 3: Яку цифру потрібно підставити замість зірочки, щоб отримати число, яке ділиться на 3:1) 28*1; 2) 4*5; 3) 1111*Розв’язання: 1) 2+8+*+1=11+*Сума має ділитись націло на 3, тому замість * можна поставити 12) 4+*+5=9+*Сума має ділитись націло на 3, тому замість * можна поставити 03)1+1+1+1+*=4+*Сума має ділитись націло 3, тому замість * можна поставити 2 Завдання 3: Яку цифру потрібно підставити замість зірочки, щоб отримати число, яке ділиться на 3: 1) 68*3; 2) 9*9; 3) 7777*27.10.2021

Приклад 4: Чи можна скласти трицифрове число, яке не містить однакових цифр і ділиться на 3, із цифр:1) 1, 2, 3; 2) 2, 3, 5; 3) 1, 0, 8 Розв’язання: Шукаємо суму цих цифер, якщо вона ділиться націло на 3, значить можна.1) 1+2+3=6, ділиться націло на 3, значить можна2) 2+3+5=10, не ділиться націло на 3, значить неможна3) 1+0+8=9, ділиться націло на 3, значить можна. Завдання 4: Чи можна скласти трицифрове число, яке не містить однакових цифр і ділиться на 3, із цифр:1) 5, 8, 3; 2) 5, 9, 7; 3) 8, 2, 127.10.2021

Контрольний тест:1. Із чисел 180, 2109, 541, 4590, 111 102, 7891 випиши ті, які: 1) діляться на 3; 2) діляться на 9;2. Яку цифру потрібно підставити замість зірочки, щоб отримати число, яке ділиться на 9: 1) 2*00; 2) *375; 3) 8*193. Запиши значення х, які кратні числу 3, при яких нерівність 45 < х < 57 буде правильною.4. Які натуральні розв’язки нерівності 657 ≤ х < 667 кратні дев’яти:а) 666б) 657; 660; 663; 666в) 657; 666г) 660; 663; 6665. Запишіть найменше трицифрове число, що ділиться націло на 9.6. Запишіть яке найменше число треба додати до числа 1275, щоб отри­мати число, яке кратне 9.27.10.2021

УРОК 3

ОЗНАКА ПОДІЛЬНОСТІ НА 4,7,8,11,1327.10.2021

27.10.2021 Розглянемо деякі ознаки подільності на 4, 7, 8, 11, 13, що не так часто зустрічаються, як на 2, 3 ,5, 9,10. Але у задачах на властивості подільності до них доводиться звертатися досить часто. Особливо це стосується олімпіадних задач.

Ознака подільності на 4 Натуральне число ділиться на 4, якщо його дві останні цифри – нулі, або складають число, що ділиться на 4. Наприклад: Число 200 ділиться на 4, оскільки останні дві цифри — 0. Число 12516 ділиться на 4, бо 16 ділиться на 4. Двозначне число ділиться на 4 тоді , коли подвоєне число десятків плюс число одиниць ділиться на 4. Наприклад: Число 76 ділиться на 4, оскільки 7∙2 + 6 = 20 , а число 20 ділиться на 4. Число 53 не ділиться на 4, бо 5∙2 + 3 = 13 ,а число 13 не ділиться на 4.

Приклад 1. Серед даних чисел назвати ті, які діляться націло на 4 : 45; 124; 2308; 312; 5452; 98; 125; 720; 1181. Розв’язок 124 (бо 24:4=6) , 2308 (бо 08:4=2) , 312 (бо 12:4=3) , 5452 (бо 52:4=13) , 720 (бо 20:4=5)Завдання 1. Серед даних чисел назвати ті, які діляться націло на 4 : 56; 230; 2448; 420; 452; 2998; 17200; 532; 1624. Приклад 2. Замість зірочки поставити таку цифру, щоб число ділилося на 4: 652* ; 126*; 43*. Розв’язок 652* : 6520, 6524, 6528126* : 1260, 1264, 126843* : 432, 436 Завдання 2. Замість зірочки поставити таку цифру, щоб число ділилося на 4: 785* ; 350*; 56*; 243*; 72*.

Приклад 3. Четверо друзів Артем, Остап, Олег та Олена зібрали в лісі жолуді та вирішили поділити їх порівну. Чи вдасться їм це зробити, якщо Остап зібрав 258 шт., Артем — у 2 рази більше, а Олег та Олена — на 132 шт. менше, ніж Артем? Дізнайтесь також, скільки всього жолудів вони зібрали?Розв’язок Остап зібрав 258 жолудів Артем зібрав 2▪258=516 жолудів. Олег та Олена зібрали по 516 – 132 = 384 жолудя. Разом — 258+516+384+384 = 1542 1542 не ділиться на 4 , бо 42 не ділиться націло на 4. Тому дітям не вдасться поділити зібрані жолуді порівну. Завдання 3. Четверо друзів Артем, Наталя , Тарас та Оксана збирали полуницю та вирішили поділити її порівну. Чи вдасться їм це зробити, якщо Артем зібрав 134 шт., Оксана та Тарас разом — у 3 рази більше, а Наталя — на 46 більше, ніж Артем? Дізнайтесь також, скільки всього полуниці вони зібрали?10/27/2021

Ознака подільності на 7 Натуральне число ділиться на 7, якщо потроєна кількість десятків, додана до кількості одиниць ділиться на 7. Наприклад: 154 перевіряємо таким чисном: 15*3+4=49, 49 ділиться на 7, отже и 154 буде кратне 7. Перевіримо число 112 за ознаками подільності 3*11+2=35; 35 ділиться на 7. Правило виконується, отже 112 ділиться на 7. Якщо сума подвоєного числа без останніх двох цифр та числа з двох останніх цифр ділиться на 7. Наприклад: 168 ділиться на 7, оскільки 2*1+68=70; 70 ділиться націло на 7

10/27/2021 Приклад 1. Яку цифру потрібно поставити замість * в записі числа 45*48, щоб отримане число ділилось на 7?Завдання 1. Яку цифру потрібно поставити замість * в записі числа 5*781, щоб отримане число ділилось на 7?Приклад 2. Чотиризначне число починається цифрами 243 і ділиться на 7. Знайти це число.

Завдання 2. Чотиризначне число починається цифрами 482 і ділиться на 7. Знайти це число. Завдання 3. Замість зірочки поставити таку цифру, щоб число ділилося на 7: 785* ; 350*; 56*; 243*; 72*.10/27/2021

Задане число ділиться на число 8, якщо три його останні цифри — нулі або число утворене його трьома останніми цифрами ділиться на 8. Наприклад: 3654168 ділиться на 8, оскільки 168 ділиться націло на 8. За цим правилом Ви не перевірите чисел до 1000, однак до них можна тричі застосувати ознаки подільності на 2. Наприклад: для числа 864 розклад на прості множники буде наступним 864/2=432; 432/2=216; 216/2=108. Отже 864 ділиться на 2*2*2=8. Ознака подільності на 8

Приклад 1. Чи є число 8 дільником 888124? Розв’язок Тут багато хто побачив спереду 8 і думає, що ділиться, але давайте перевіримо правило 124/8=62*2=31*2*2=31*4. Бачимо, що на 4 число ще ділиться, а от на 8 без остачі ніяк. Отже 888124 на 8 націло не ділиться. Завдання 1. Чи є число 8 дільником 758624?Приклад 2. Серед даних чисел назвати ті, які діляться на 8 : 45032; 12400; 23088; 3120; 5856; 19008; 12047.27.10.2021

27.10.2021 Завдання 2. Серед даних чисел назвати ті, які діляться на 8 : 4532; 124; 23048; 3440; 7556; 17028; 12000. Приклад 3. Замість зірочки поставити такі цифри, щоб число ділилося на 8: 652*** ; 126***; 76***; 124*; 43*. Завдання 3. Замість зірочки поставити такі цифри, щоб число ділилося на 8: 8572*** ; 124***; 768***; 4*; 38*. Завдання 4. Шестицифрове число ділиться на 8. Яку найбільшу суму цифр воно може мати?

27.10.2021 Завдання 4. Маленькі мавпочки втекли із зоопарку і прибігли до продуктового магазину. Там вони знайшли 2 ящика бананів - великий і малий. У великому ящику було 5430 бананів, а в маленькому - 3034 бананів. Вони змогли поділити порівну банани з великого і з маленького ящиків. Скільки було мавпочок, якщо їх було більше 4, але менше 10?

Ознака подільності на 11 Натуральне число ділиться на 11, якщо на 11 ділиться сума чисел, що утворена парами цифр запису числа, починаючи з одиниць. Наприклад: 103785, складаємо суму: 10+37+85=132, 01+32=33, 33 ділиться на 11, отже й число 103785 ділиться на 11. Число ділиться на 11, якщо різниця суми цифр які займають парні місця та суми цифр які займають непарні, ділиться на 11. Наприклад: 103785 ділиться на 11, бо (1+3+8) – (0+7+5) = 12 – 12 = 0, а 0 ділиться на 7.

10/27/2021 Приклад 1. До числа 10 справа і зліва приписали по одній цифрі так , щоб це число було кратне 11. Виберіть це число з відповідей.1)1102 2)2101 3)7106 4)8105 Розв’язок Завдання 2. До числа 12 справа і зліва приписали по одній цифрі так , щоб це число було кратне 11. Виберіть це число з відповідей.1)1122 2)2121 3)7128 4)8125 Приклад 2. Чи ділиться число 784454 націло на 11. Розв’язок Оскільки сума пар цифр числа 784454, 78 + 44 + 54 = 176, 01+76 = 77, 77 ділиться націло на 11, тому і саме число ділиться на 11. Завдання 2. Чи число 376449 ділиться націло на 11.

Ознака подільності на 13 Натуральне число ділиться на 13, якщо сума числа десятків з кількістю одиниць, помноженою на 4, ділиться на 13. Наприклад: число 845 містить 84 десятки й 5 одиниць, складаємо суму 84+5*4=104, далі: 10+4*4=26 – ділиться на 13, отже й число 845 ділиться на 13.

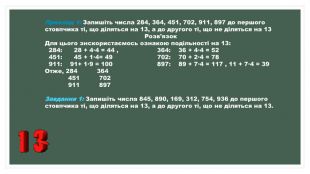
Приклад 1: Запишіть числа 284, 364, 451, 702, 911, 897 до першого стовпчика ті, що діляться на 13, а до другого ті, що не діляться на 13 Розв’язок Для цього знскористаємось ознакою подільності на 13: 284: 28 + 4∙4 = 44 , 364: 36 + 4∙4 = 52 451: 45 + 1∙4= 49 702: 70 + 2∙4 = 78 911: 91+ 1∙9 = 100 897: 89 + 7∙4 = 117 , 11 + 7∙4 = 39 Отже, 284 364 451 702 911 897 Завдання 1: Запишіть числа 845, 890, 169, 312, 754, 936 до першого стовпчика ті, що діляться на 13, а до другого ті, що не діляться на 13.

Приклад 2. Чи ділиться число 554 націло на 13. Розв’язання : Оскільки сума пар цифр числа 554, 55 + 4∙4 = 71, 71 не ділиться націло на 13, тому і саме число ділиться на 13. Завдання 2. Чи число 559 ділиться націло на 13.10/27/2021

Контрольний тест1. Чи число 789 ділиться націло на 13.2. Із чисел 56; 230; 2048; 420; 452; 2998; 17200; 532; 1000 випиши ті, які: 1) діляться на 4; 2) діляться на 8;3. У Петрика було більше ніж 30, але менше ніж 50 камінчиків. Коли він розклав камінчики у купки по 4 штук, то один камінчик залишився, а коли він розклав їх у купки по 7 штуки, то залишилось 2 камінчики. Яка кількість камінчиків була в Петрика?А) 41; Б) 35; В) 37; Г) 49.4. Запиши значення х, які кратні числу 7, при яких нерівність 148< х <257 буде правильною.5. Шестизначне число закінчується цифрами 137 і ділиться на 7, 11 та 13. Знайти це число.

УРОК 4

Подільність суми, різниці і добутку

Теореми про подільність суми, різниці і добутку: Теорема 1: Якщо кожен із доданків ділиться на задане число, то й сумаділиться на це число. Теорема 2: Якщо зменшуване і від’ємник діляться на дане число, то йрізниця ділиться на це число. Теорема 3: Якщо у добутку кількох чисел хоч один із множниківділиться на задане число, то й добуток ділиться на цечисло.

Теорема 1: Якщо кожен із доданків ділиться на задане число, то й сумаділиться на це число. Наприклад: Розгляньмо суму чисел 12 і 21, тобто (12+21). У цій сумі кожен із доданків ділиться на 3. Перевіряючи подільність суми на 3, отримаємо, що сума 33 теж ділиться на 3. Приклад 1: Перевірити чи сума чисел ділиться на 3:1) (15+18);2) (12+22). Розв'язання:1) 15 ділиться націло на 3, та 18 ділиться на 3, тоді (15+18) ділиться на 3.2)12 ділиться націло на 3, а 22 не ділиться на 3, тоді (12+22) не ділиться на 3. Завдання 1: Перевірити чи сума чисел ділиться на 4:1) (18+28);2) (16+44).

Приклад 2: Зазначте натуральне число х, таке, щоб сума (26+х) ділилась на 2 :1) 53; 2) 45; 3) 42; 4) 67. Розв'язання: 1) (26+53) не ділиться на 2, тому, що 53 не ділиться на 2.2) (26+45) не ділиться на 2, тому, що 45 не ділиться на 2.3) (26+42) ділиться на 2, тому, що і 26 і 42 ділиться на 2.4) (26+ 67) не ділиться на 2, тому що 67 не ділиться на 2. Завдання 2: Зазначте натуральне число х, таке, щоб сума (х+72) ділилась на 9 :1) 34; 2) 42; 3) 39; 4)81.

Приклад 3: У Андрія було 4 груші, мама дала йому ще 16 груш. Чи зможе Андрій роздати порівну груші своїм чотирьом друзям?Розв'язання: (4+16)- всього груш у Андрія 4 ділиться на 4 та 16 ділиться на 4. Отже, Андрій зможе роздати груші порівну своїм друзям. Завдання 3: У шкільних змаганнях беруть участь 27 учнів 9-А класу та 36 учнів 9-Б класу. Чи можна поділити цих учнів на 9 команд з рівною кількістю учнів.

Теорема 2: Якщо зменшуване і від’ємник діляться на дане число, то йрізниця ділиться на це число. Наприклад: Розглянемо різницю чисел 45 та 27, тобто (45-27). У цій різниці і зменшуване і від'ємник діляться на 9, значить і різниця ділиться на 9. Приклад 1: Перевірити чи різниця чисел ділиться на 5:1) (46-45);2) (90-105). Розв'язання: 1) 46 не ділиться націло на 5, отже різниця не ділиться на 5;2) 90 ділиться націло на 5, та 105 ділиться націло на 5, отже різниця ділиться на 5. Завдання 1: Перевірити чи різниця чисел ділиться на 8:1) (48-64);2) (42-72).

Приклад 2: Зазначте натуральне число х, таке, щоб різниця (х-36) ділилась на 6:1) 126; 2) 45; 3) 112; 4) 64. Розв'язання: 1) (126-36) ділиться націло на 6, бо 126 ділиться націло на 6, та 36 також ділиться націло на 6.2) (45-36) не ділиться націло на 6, бо 45 не ділиться націло на 6.3) (112-36) не ділиться націло на 6, бо 112 не ділиться націло на 6.4) ( 64-36) не ділиться націло на 6, бо 64 не ділиться націло на 6. Завдання 2: Зазначте натуральне число х, таке щоб різниця чисел (184-х) ділилась націло на 4:1) 86; 2) 62; 3) 84; 4)126.

Приклад 3: Вчитель задав учням 44 вправи, на уроці встигли зробити 12 вправ з цього списку. Чи встигнуть учні зробити вправи, що залишилися за 4 дні, якщо робитимуть однакову кількість завдань кожного дня. Розв'язання: (44-12)ділиться на 4, тому що і 44 і 12 ділиться націло на 4. Отже, учні встигнуть зробити завдання. Завдання 3: На вулиці гралось 84 дитини, 18 дітей забрали додому. Чи зможуть діти, що залишилися поділитись на 6 команди з рівною кількістю гравців.

Теорема 3: Якщо у добутку кількох чисел хоч один із множниківділиться на задане число, то й добуток ділиться на цечисло. Наприклад: Розгляньмо добуток чисел 24⋅73=1752. Один із множників у цьому добутку ділиться на 3, тобто 24:3=8. Можна переконатися, що й весь добуток ділиться на 3, тобто 1752:3=584. Приклад 1: Вказати який з добутків чисел ділиться націло на 5:1) 45⋅224; 2)22⋅68; 3) 226⋅668; 4) 779⋅669. Розв'язання: 1) Ділиться націло на 5, тому, що 45 ділиться націло на 5.2) Не ділиться націло на 5, тому, що ні 22, ні 68 не ділиться націло на 5.3) Не ділиться націло на 5, тому, що ні 226, ні 668 не ділиться націло на 5. 4) Не ділиться націло на 5, тому, що ні 779, ні 669 не ділиться націло на 5. Завдання 1: Вказати який з добутків ділиться націло на 2:1) 339⋅115; 2) 13⋅55⋅78; 3)45⋅13; 4) 25⋅77⋅9.

Приклад 2: З’єднати добутки та числа, яким вони кратні:1) 22⋅13; а) кратне числам 2 та 3;2) 12⋅33⋅7; б) кратне числам 2 та 5;3) 55⋅5⋅45; в) кратне тільки числу 2;4) 50⋅5; г) кратне тільки числу 5. Розв'язання: 1) Кратне тільки числу 2, тому, що 22 ділиться націло на 2, а 13 не ділиться націло ні на 3, ні на 5.2) Кратне числам 2 та 3, тому, що 12 ділиться націло на 2, 33 ділиться націло на 3, а 7 не ділиться націло на 5.3) Кратне тільки числу 5, тому, що і 55 і 5 і 45 ділиться націло на 5.4) Кратне числу 2 та 5, тому, що 50 ділиться націло і на 2 і на 5, а 5 ділиться націло на 5. Завдання 2: З’єднати добутки та числа, яким вони кратні:1) 72⋅7; а) кратне тільки числу 7;2) 20⋅2⋅10; б) кратне числу 2 та 7;3) 7⋅77; в) кратне числу 2 та 5.

Контрольний тест:1. Не виконуючи обчислень, виберіть, якому числу кратний даний добуток 25⋅39:1) 3; 2) 2; 3) 8.2. Зазнач натуральне значення x, щоб різниця 78−x ділилась на 2:1) 4; 2) 7; 3) 5.3. В одному пакеті було 15 горіхів, а в другому — 20. Чи можливо ці горіхи поділити порівну між 5 друзями? 4. Відомо, що m і n — два різних простих числа, більших від 2. Чи буде правильним твердження: їх різниця — парне число.5. У книжці 384 сторінки та 126 сторінки вступу. Галя повинна віддати книгу подружці через 6 днів, чи зможе дівчина прочитати книгу, якщо читатиме однакову кількість сторінок кожного дня.6. З’єднати вирази з числами, яким вони кратні:1)(21+18); а) кратне числу 5;2) 40⋅25; б) кратне числу 2;3) (32-26); в) кратне числу 3 г) кратне чслу 5 і 2.

КОНТРОЛЬНІ ЗАПИТАННЯ1. Які з цих чисел діляться : 354,591,876,543,911,322,678,239,1001,788 1) на 2; 2) на 3; 3) на 4.2. Які з цих чисел : 445,189,700,1000,81,555,909,343,121,6151)діляться на 5; 2)діляться на 9; 3)діляться на 10.3. Яку цифру потрібно поставити замість зірочки , щоб отримати число , яке ділиться на 3.1)330* , 2)141* , 3)99*4. П΄ятицифрове число 24х8у ділиться на 4, 5 і 9. Чому дорівнює сума цифр х і у *5. Запишіть будь-яке чотирицифрове число , яке кратне 10.6. Запишіть значення х ,які кратні числу 11 , при яких нерівність 100<х<300 буде правильною.

10/27/20217. Знайти усі числа х та у, при яких число 3х5у 1)ділиться на 9; 2)ділиться на 10.8. Ліворуч і праворуч від числа 10 допишіть по одній цифрі так, щоб утворилося чотирицифрове число, кратне 3. А) 3 і 6;   Б) 4 і 4;   В) 2 і 7;    Г) 8 і 2.9. У Петрика було більше ніж 30, але менше ніж 50 камінчиків. Коли він розклав камінчики у купки по 5 штук, то один камінчик залишився, а коли він розклав їх у купки по 3 штуки, то залишилось 2 камінчики. Яка кількість камінчиків була в Петрика?А) 41;   Б) 45;   В) 36;    Г) 46.10. Не виконуючи дій і користуючись ознаками подільності, з’ясуйте, чи добуток 6*23*75 ділиться на 5; на 9; на 10.11. Зазначте натуральне значення х , щоб сума 59+х ділилась на 2.1)2; 2)5; 3)412. Знайдіть найменше складене число , яке не ділиться на жодне із натуральних чисел від 2 до 10.