Прикладні задачі до теми СЛР з двома змінними

ПРИКЛАДНІ ЗАДАЧІ Прикладна задача — це задача, що виникла поза математикою, але яку можна розвґязати математичними засобами.

Пам'ятай! Коли ми розв'язуємо задачу за допомогою рівняння чи системи двох рівнянь, зручніше шукане в задачі число брати за невідоме. Розв'язати систему рівнянь з двома змінними означає знайти таку пару чисел, що є розв'язком цих рівнянь або ж довести, що такої пари не існує чи таких пар безліч.

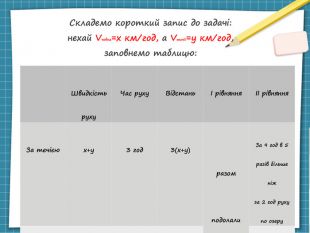
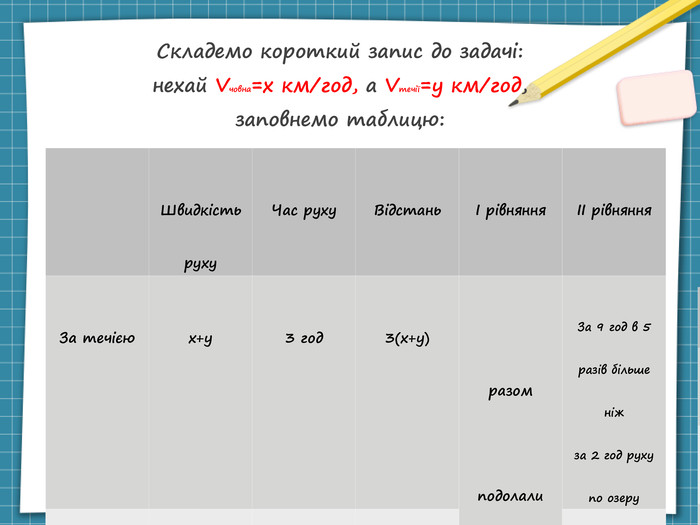
Вправа 1089 Човен за 3 години руху за течією і 2 години руху проти течії долає 92 км. За 9 год за течією човен долає відстань у 5 разів більшу, ніж за 2 години руху по озеру. Знайдіть власну швидкість човна та швидкість течії. Зосередся: згадай визначення: власна швидкість човна, швидкість течії, швидкість човна за течією та проти течії; застосуй систему рівнянь з двома змінними; склади рівняння для системи.

Складемо короткий запис до задачі: нехай Vчовна=x км/год, а Vтечії=y км/год, заповнемо таблицю: Швидкість руху Час руху Відстань За течією x+y 3 години 3(x+y) 2(x-y) Проти течії x-y 2 години Швидкість руху Час руху Відстань І рівняння ІІ рівняння За течією x+y 3 год 3(x+y) разом подолали 92 км За 9 год в 5 разів більше ніж за 2 год руху по озеру Проти течії x-y 2 год 2(x-y)

3(x+y)+2(x-y)=92, 9(x+y)=5·2x; розкриваємо дужки 3x+3y+2x-2y=92, 9x+9y=10x; 5x+y=92, x=9y; 5·9y+y=92, x=9y; 46y=92, x=9y; y=2, x=9·2=18; зводимо подібні доданки підставимо значення Х у перше рівняння розв'язуємо перше рівняння... Отже, маємо: Vчовна=18км/год Vтечії=2км/год.

Вправа 1091 З пункту А і В, відстань між якими 168 км, одночасно вирушають велосипедист і мотоцикліст. Якщо вони будуть рухатися на зустріч один одному, то зустрінуться через 3 години. А якщо рухатимуться в одному напрямі, то мотоцикліст наздожене велосипедиста через 6 год. Знайдіть швидкість кожного з них. Зосередся: згадай визначення: рух в одному напрямі та протилежних; відстань між обґєктами в обох випадках; застосуй систему рівнянь з двома змінними; склади рівняння для системи.

Введемо заміну... Оскільки нам потрібно знайти швидкості велосипедиста та мотоцикліста, то нехай Vвел=x км/год, а Vмот=yкм/год. Отже, якщо вони рухатимуться на зустріч один одному, то можна скласти рівняння: 3x+3y=168. А якщо рухатимуться в одному напрямку, то матимемо дане рівняння: 6y-6x=168. Тому складемо і розвґяжемо систему рівнянь: 3x+3y=168, 6y-6x=168.

3x+3y=168, 6y-6x=168; винесемо спільні множники зліва в обох частинах рівнянь... 3(x+y)=168, 6(y-x)=168; x+y=56, y-x=28; 2y=84, x+y=56; y=42, x+42=56; y=42, x=56-42=14; спростимо рівняння... додамо почленно рівняння... знайдемо значення Y Отже, маємо: Vмот=42км/год Vвел=14км/год.

Вправа 1092 Сума двох чисел дорівнює 62. Знайдіть кожне із чисел, якщо 70% від одного і 60% від другого разом складають 39,6. Зосередся: згадай визначення: відсоток від числа; сума чисел; застосуй систему рівнянь з двома змінними; склади рівняння для системи. Введемо заміну... Нехай перше число дорівнює X, а друге число -Y. Так як сума даних чисел дорівнює 62, маємо перше рівняння: x+y=62 Оскільки сума 70% від X та 60% від Y дорівнює 39,6, то маємо рівняння: 0,7x +0,6 y=39,6 Складемо та розвґяжемо систему рівнянь...

x+y=62, 0,7x+0,6y=39,6 виразимо з першого рівняння значення X через Y... x=62-y, 0,7(62-y)+0,6y=39,6; x=62-y, 43,4-0,7y+0,6y=39,6; x=62-y, -0,1y=-3,8; y=38, x=62-38; x=24, y=38. спростимо друге рівняння... спрощуємо друге рівняння... знайдемо значення Y Отже, маємо: перше число 24, а друге —38.

Вправа 1100 Змішали два види цукерок вартістю 45 грн і 54 грн за кілограм, після чого утворилося 25 кг суміші вартістю 48 грн 96 коп. за кілограм. По скільки кілограмів цукерок кожного виду взяли для суміші? Зосередся: згадай визначення: вартість; вага; вартість покупки; застосуй систему рівнянь з двома змінними; склади рівняння для системи.

Введемо заміну... Оскільки нам відомо, що було два види цукерок, то нехай одного виду цукерок було X кг, а іншого Y кг. Тоді, якщо загальна вага суміші цукерок була 25 кг, то складемо перше рівняння: x+y=25. А так як вартість суміші цукерок за кілограм стала 48 грн 96 коп, то маємо рівняння: 45x+54y=48,96(x+y). Тому складемо і розвґяжемо систему рівнянь: x+y=25, 45x+54y=48,96(x+y).

x+y=25, 45x+54y=48,96(x+y) виразимо з першого рівняння значення X через Y... x=25-y, 45(25-y)+54y=48,96(25-y+y); x=25-y, 1125-45y+54y=1224; x=25-y, 9y=99; y=11, x=25-11; x=14, y=11. спростимо друге рівняння... розв'яжемо друге рівняння... знайдемо значення Y, Та розв'яжемо друге рівняня... Отже, маємо: першого виду цукерок -14 кг, а другого —11кг.

Вправа 1102 У двох бідонах разом було 75 л олії. Після того як половину олії з першого бідона перелили в другий, олії в другому стало в 4 рази більше, ніж у першому. По скільки олії було в кожному бідоні спочатку? Зосередся: згадай визначення: дріб від числа; застосуй систему рівнянь з двома змінними; склади рівняння для системи. Введемо заміну... Нехай в першому бідоні було X л олії, а в другому бідоні -Yл. Так як у двох бідонах разом було 75 л олії, то маємо перше рівняння: x+y=75 Оскільки з першого бідона перелили половину олії (0,5x ) до другого і в другому стало в 4 рази більше ніж в першому, то маємо рівняння: y+0,5x=4·0,5x Складемо та розвґяжемо систему рівнянь...

x+y=75, y+0,5x=4·0,5x; виразимо з першого рівняння значення X через Y та спростимо друге рівняння... x=75-y, y+0,5x=2x; x=75-y, y+0,5(75-y)=2(75-y); x=75-y, y+37,5-0,5y=150-2y; x=75-y, y-0,5y+2y=150-37,5; x=75-y=75-45=30, y=45. підставимо значення X в друге рівняння та розв'яжемо його... спрощуємо друге рівняння та знаходимо значення X і Y... Отже, маємо: В першому бідоні 30 л олії, а в другому —45 л.

Вправа 1108 По скільки грамів кожного з 2-відсоткового і 6-відсоткового розчинів солі треба взяти, щоб з них одержати 200 г 5-відсоткового розчину? Зосередся: згадай визначення: розчин; відсоток від числа; маса; застосуй систему рівнянь з двома змінними; склади рівняння для системи. Введемо заміну... Нехай було x г 2% розчину та y г 6% розчину. Так як всього отримали розчин вагою 200 г, то складемо рівняння: x+y=200 Оскільки в першому розчині міститься 2% солі, в другому —6% солі, а в отриманому розчині —5%, то маємо рівняння: 0,2x+0,6y=0,5(x+y) Складемо та розвґяжемо систему рівнянь...

x+y=200, 0,2x+0,6y=0,5(x+y) виразимо з першого рівняння значення X через Y... x=200-y, 0,2(200-y)+0,6y=0,5(200-y+y); x=200-y, 40-0,2y+0,6y=100; x=200-y, 0,4y=60; y=150, x=200-150=50; x=50, y=150. спростимо друге рівняння... спрощуємо друге рівняння... знайдемо значення Y Отже, маємо: маса 2% розчину —50 г, а маса 6%—150г.

Домашнє завдання: Опрацювати § 30 та виконати впр. 1082, 1084, 1090, 1093, 1099, 1101, 1105