Прикладні задачі з теми: «Об’єм призми»

Задача. Володимир мріяв про акваріум із золотими рибками. На день народження йому подарували акваріум у формі прямокутного паралелепіпеда з вимірами: 34 см, 80 см, 50 см. Перед хлопцем постала задача: яку максимально можливу кількість золотих рибок він зможе утримувати в цьому акваріумі, якщо норма води на одну таку рибку становить 12 л? Допоможіть Володимирові розв'язати задачу!

Відповідь: 11 рибок.

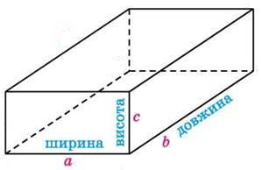
Задача. Класні кімнати повинні бути розраховані так, щоб на кожного учня припадало не менше 6 м повітря. Скільки учнів можна розмістити у кабінеті математики, який має форму прямокутного паралелепіпеда з вимірами 8,8 м, 6,4 м і 3,2 м не порушуючи санітарних норм?

Розв’язання

1) (м) −об’єм класної кімнати або об’єм повітря в кімнаті.

2) 180,224 : 6 30,04 30 ( уч.) − можна розмістити у кабінеті математики.

Відповідь: 30 учнів.

Задача. Цукор-рафінад виготовляють у вигляді шматочків форми прямокутного паралелепіпеда розміром 24х24х10мм. Скільки шматочків цукру повинно міститись у пачці масою 0,5 кг? Питома вага цукру 1,2 г/см².

Відповідь. ≈70 штук.

Задача. Яку масу мають 350 цеглин, якщо довжина кожної цеглини 230 мм, ширина-114 мм, товщина-65 мм? ρ=1800кг/м³. 

Відповідь: 107,709 кг

Задача. Вважають, що шкідливо залишати на ніч квіти в кімнаті, тому що вони поглинають О₂ , необхідний для дихання людини. Щоб, довести, чи вірна ця думка, обчисліть, до якої величини знизиться вміст кисню у кімнаті розміром 5м × 3м × 3м за 10 годин внаслідок дихання рослин масою 4 кг і середньою інтенсивність дихання 12 мл О₂ на 1г за добу (умови нормальні). Початковий вміст кисню 21%.

Розв’язання:

Знайдемо об’єм кімнати: V = abc = 5 · 3 · 3 = 45 м³.

У кімнаті об’ємом 45 м³ за нормального тиску міститься 21% О₂ ,

що складає : 45 · 0,21 = 9,45м³.

За 10 годин рослини поглинуть кисню:

12 мл • 4000 г • 10 : 24= 20000 мл = 20л О_{2 =} 0,02 м³ О₂.

Відповідь: кімнатні рослини шкоди диханню людини не завдають.

Задача. Класні кімнати повинні бути розраховані так, щоб на кожного учня припадало не менше 6 м повітря. Скільки учнів можна розмістити у кабінеті математики, який має форму прямокутного паралелепіпеда з вимірами 8,8 м, 6,4 м і 3,2 м не порушуючи санітарних норм?

Розв’язання

1) (м) −об’єм класної кімнати або об’єм повітря в кімнаті.

2) 180,224 : 6 30,04 30 ( уч.) − можна розмістити у кабінеті математики.

Відповідь: 30 учнів.

Задача. Кубатура однієї кімнати будівлі дорівнює 120м³ . Обчислити кубатуру іншої кімнати, якщо її ширина в 1,5 рази більша від ширини першої, а довжина в 3 рази менша. (Відповідь: 60м³)

Задача. 1 м³ золота важить приблизно 19 т. Чи може людина підняти куб золота, ребро якого 30 см (аргументуйте відповідь)? ((Відповідь: ні, бо такий куб важить 513 кг)

Задача. Резервуар для води слід встановити на майданчику трикутної форми, що слугуватиме для нього дном. Якою має бути висота резервуара? Ємність резервуара 10 м³, площа майданчика  5 м².

Розв’язання.

1. Яку геометричну фігуру вам нагадує резервуар (пряму трикутну призму)?
2. Чи відомий об’єм цієї фігури (10 м³)?
3. Чому дорівнює площа основи фігури (5 м²)?

Будемо розглядати резервуар як пряму призму об’ємом 10 м³, основою якого є трикутник площею  5 м².

4. За допомогою якої формули знаходимо об’єм призми (V =Sосн ⋅H)?

Тоді V =Sосн ⋅H, де H – шукана висота,  Sосн =5 (м²), V=10 м³.

5. Як за допомогою цієї формули знайти висоту ()?

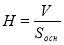Отже:

Відповідь: 2 м.

Задача. Залізничний насип у перерізі має форму рівнобічної трапеції з основами 12м та 4м і бічною стороною 5м. Скільки кубічних метрів землі містить 3км насипу?

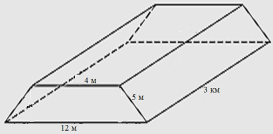
Відповідь: 72000м³