Проект "Методика додавання і віднімання, множення і ділення багатоцифрових чисел"

Тема проекту: Методика додавання і віднімання, множення і ділення багатоцифрових чисел. Підготувала: Вчитель початкових класів. Денисенко З. В.

Основні завдання вчителя під час вивчення цієї теми:-сформувати поняття про нову лічильну одиницю - 1000 (тисячу), як одиницю 2 класу;- виходячи з поняття класу, навчити утворювати читати і записувати багатоцифрові числа;- узагальнити знання дітей про нумерацію цілих невід'ємних чисел.

Корисно спочатку повідомити дітям, що вони незабаром вчитимуться лічити до мільйона і записувати багатоцифрові числа, а потім дати кілька усних завдань з виходом за тисячу. Такий підхід викличе інтерес у дітей до цієї теми, активізуватиме їхню самостійну пізнавальну діяльність.

В усній нумерації, крім порозрядної лічби, застосовують ще спосіб групування розрядів у класи. Щоб прочитати багатоцифрове число, його запис розбивають на групи по три цифри. Три перші цифри справа утворюють клас одиниць, три наступні цифри — клас тисяч. Так утворюють класи і для чисел, більших за мільйон.

При читанні чисел називають число одиниць кожного класу і назву класу. Наприклад, 237 153 — двісті тридцять сім тисяч сто п'ятдесят три (одиниці). Назву класу одиниць здебільшого не називають.

Письмова нумерація ґрунтується на помісцевому значенні цифр (позиційний принцип). Значення цифри у запису числа змінюється залежно від того, яке місце воно займає. Якщо цифру переставити на одне місце вліво, її значення збільшується в 10 разів, а якщо на одне місце вправо, то її значення зменшується в 10 разів. Наприклад: у числі 237 цифра 3 означає 3 десятки, тобто 30; у числі 327 цифра 3 означає 3 сотні, тобто 300; у числі 273 ця цифра означає 3 одиниці.

Письмова нумерація побудована на принципі додавання, оскільки запис числа є не що інше як запис суми його розрядних чисел. Наприклад: 25 527 = 20 000 + 5 000 + 500 + 20 + 7.

Нумерацію багатоцифрових чисел і дії над ними виділено в окремий концентр, тому що нумерація чисел за межами 1000 має свої особливості: багатоцифрові числа утворюють, називають, записують, виходячи з поняття не тільки розряду, але й класу.

Арифметичні дії над багатоцифровими числами виконують з використанням як усних, так і письмових прийомів обчислення. Вироблення свідомих і міцних навичок письмових обчислень – одне з основних завдань вивчення дій над багатоцифровими числами. Порядок вивчення питань у концентрі «Багатоцифрові числа» такий: нумерація, додавання і віднімання, множення і ділення. Одночасно розглядають задачі, вимірювання величин, алгебраїчний і геометричний матеріал

У вивченні нумерації багатоцифрових чисел є таких два основних підходи: а) числа вивчають у порядку збільшення (нарощування) розрядів, тобто починають вивчати чотирицифрові числа, потім п'яти- і шестицифрові, а вже після цього дають поняття про клас; б) числа вивчають за класами, після першого класу йде другий, а потім вивчають перших два класи разом. Кожний з підходів має як переваги, так і слабкі місця. В чинній програмі і діючих підручниках для початкової школи реалізується перший підхід. Особливістю вивчення нумерації багатоцифрових чисел є те, що усну і письмову нумерації опрацьовують одночасно

Під час ознайомлення з письмовим додаванням і відніманням багатоцифрових чисел учні розв’язують такі приклади, де кожний наступний містить у собі попередній, наприклад: 752 4752 54752 + 246 + 3246 + 43246 Розв’язавши такі приклади, учні самостійно зроблять висновок про те, що усне додавання і віднімання багатоцифрових чисел виконують так само, як і письмове додавання і віднімання трицифрових чисел.

Вивчаючи додавання і віднімання багатоцифрових чисел, важливо приділити увагу усним прийомам виконання цих дій; інакше кажучи, опанувавши письмові прийоми обчислень, діти починають застосовувати їх як для письмових, так і для усних випадків. Для цього, розв’язуючи приклади, треба надавати учням можливість самостійно вибирати приклади, які вони можуть розв’язати усно, і лише найважчі приклади розв’язувати за допомогою письмових прийомів.

Основне завдання теми полягає у формуванні навичок письмового множення і ділення багатоцифрових чисел. Навички мають бути доведені до автоматизму, але учні повинні вміти пояснювати виконувані дії. Треба систематизувати знання учнів про дії множення і ділення та їхні властивості, про взаємозв’язок між результатами і компонентами дій, про зміну добутку й частки від зміни одного з компонентів; засвоїти основні усні і письмові прийоми множення й ділення; опанувати відповідні обчислювальні уміння і навички.

Алгоритми дій множення і ділення різні. Тому прийоми виконання дій вводять почергово: після вивчення одного випадку множення вивчають аналогічний випадок ділення. Опрацювання матеріалу має 3 етапи: множення і ділення на одноцифрове число; множення і ділення на дво- і трицифрові розрядні числа; множення і ділення на двоцифрове число.

Виділяють окремі випадки множення і ділення багатоцифрових чисел. До окремих випадків множення належать випадки з нулями (нулем) у множниках: перший або другий множник закінчується нулями (87600 ∙ 4 і 376 ∙ 240), нулі в середині другого множника (875 ∙ 304), а також різні поєднання цих випадків (170 ∙ 230; 1360 ∙ 103). До окремих випадків ділення належать випадки з нулями (нулем) у частці: частка закінчується нулями (227 200: 4 = 56800); нулі в середині частки (72450 : 7 = 10350)

Давайте розглянемо типові помилки учнів при формуванні обчислювальних навичок і методичні прийоми їх попередження та усунення. При виконанні прикладів на дію додавання, школярі можуть допускати такі суттєві помилки :1) правильно: неправильно: 528 528 +275 +275 803 7938 + 5 = 13 = 10 + 3 Тобто 10 одиниць першого розряду є одиницею другого розряду. Учні забувають одиницю додавати до 9.2) неправильно: 528 + 275 79138 + 5 = 13, тобто учні в перший розряд вписують дві цифри: 1 і 3, а кожен розряд має по одній цифрі.

3) неправильно: правильно: 389 389 + 27 + 27 Неправильно підписують розряд під розрядом.4) змішування дій додавання і віднімання:298 + 144 = 154 (442) 289 – 144 = 433 (145) Діти переплутують знаки, замість додавання виконують дію віднімання, і навпаки.

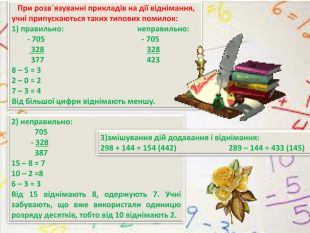
При розв`язуванні прикладів на дії віднімання, учні припускаються таких типових помилок:1) правильно: неправильно: - 705 - 705 328 328 377 4238 – 5 = 32 – 0 = 27 – 3 = 4 Від більшої цифри віднімають меншу.2) неправильно: 705 - 328 38715 – 8 = 710 – 2 =86 – 3 = 3 Від 15 віднімають 8, одержують 7. Учні забувають, що вже використали одиницю розряду десятків, тобто від 10 віднімають 2.3)змішування дій додавання і віднімання:298 + 144 = 154 (442) 289 – 144 = 433 (145)

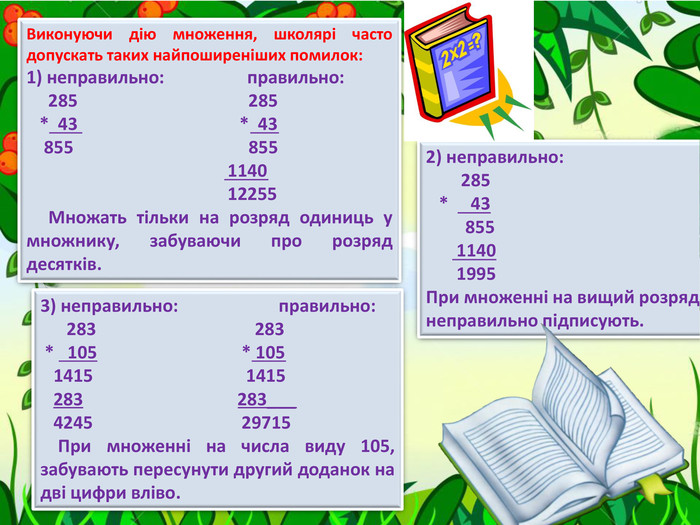
Виконуючи дію множення, школярі часто допускать таких найпоширеніших помилок:1) неправильно: правильно: 285 285 * 43 * 43 855 855 1140 12255 Множать тільки на розряд одиниць у множнику, забуваючи про розряд десятків.2) неправильно: 285 * 43 855 1140 1995 При множенні на вищий розряд неправильно підписують.3) неправильно: правильно: 283 283 * 105 * 105 1415 1415 283 283___ 4245 29715 При множенні на числа виду 105, забувають пересунути другий доданок на дві цифри вліво.

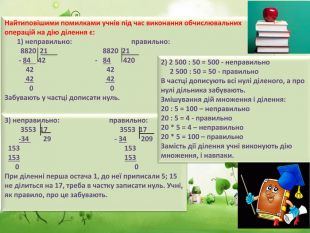
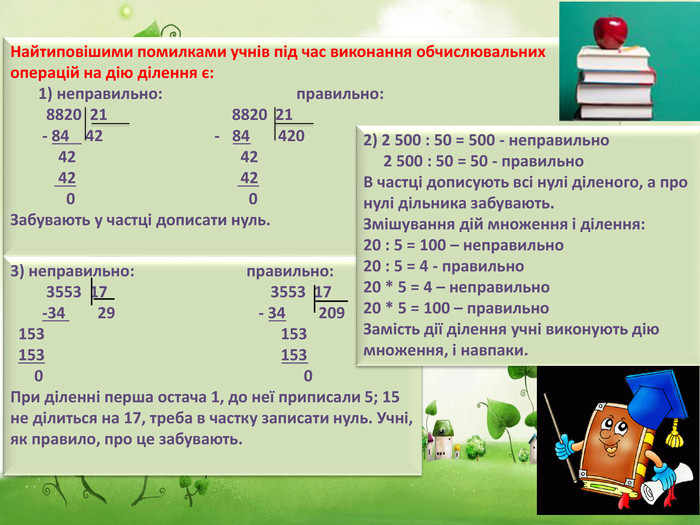
Найтиповішими помилками учнів під час виконання обчислювальних операцій на дію ділення є: 1) неправильно: правильно: 8820 21 8820 21 - 84 42 - 84 420 42 42 42 42 0 0 Забувають у частці дописати нуль.3) неправильно: правильно: 3553 17 3553 17 -34 29 - 34 209 153 153 153 153 0 0 При діленні перша остача 1, до неї приписали 5; 15 не ділиться на 17, треба в частку записати нуль. Учні, як правило, про це забувають.2) 2 500 : 50 = 500 - неправильно 2 500 : 50 = 50 - правильно. В частці дописують всі нулі діленого, а про нулі дільника забувають. Змішування дій множення і ділення:20 : 5 = 100 – неправильно20 : 5 = 4 - правильно20 * 5 = 4 – неправильно20 * 5 = 100 – правильно. Замість дії ділення учні виконують дію множення, і навпаки.

Застосування прийомів множення багатоцифрових чисел на одноцифрові при розв’язуванні прикладів і задач (Урок-КВК. Математика. 4-й клас)

Мета: закріплювати вміння учнів розв’язувати задачі та приклади на застосування алгоритму множення багатоцифрових чисел на одноцифрові; вдосконалювати обчислювальні навички і вміння, розв’язувати задачі на рух; розвивати логічне мислення, мовлення, пам’ять, увагу, кмітливість; прищеплювати інтерес до предмета. Обладнання: картки із завданнями, нагороди переможцям.

МАТЕРИК УСНОГО РАХУНКУМАТЕРИК ЗАДАЧНИЙМАТЕРИК МАТЕМАТИЧНОГОДИКТАНТУМАТЕРИК ПРИКЛАДНИЙМАТЕРИК ВІДПОЧИВАЙКАМАТЕРИК МАТЕМАТИЧНОЇ ЕСТАФЕТИ

І. Організація класу. Клас поділяється на три команди. Кожна команда обирає собі капітана і назву («Пізнайки», «Всезнайки», «Чомучки»).ІІ. Оголошення теми і завдань уроку.- Сьогодні у нас буде незвичайний урок-змагання, де кожен із вас зможе продемонструвати свої вміння розв’язувати приклади і задачі, а також працювати в команді.ІІІ. Повторення вивченого матеріалу.1. Розминка (усний рахунок). Задачі на рух.а) За кожну правильну відповідь команда отримує 2 бали. Велосипедист рухався зі швидкістю 15 км/год і був у дорозі 4 год. Яку відстань він подолав?б) Поїзд за 4 год проїхав 224 км. З якою швидкістю він рухався?в) Швидкість людини 5 км/год, а поїзда – 120 км/год. У скільки разів швидкість поїзда більша, ніж швидкість людини? Хід уроку15 · 4 = 60 (км)224 : 4 = 56 (км/год)120 : 5 = 24 (р.)

УСНИЙ РАХУНОК24500010000804500001005590800000:+++-·250559910800320

ПЕРЕВІРЯЄМОЗНАЙДІТЬ СУМУ ЧИСЕЛ8000 ТА 200010000

Доданок - 6000. Сума - 10000. Знайдіть другий доданок4000

Половину числа 500 збільшіть на 10260

На лісовій галявиніграли звірі і синиця. Усього 10 ніг. Скільки було звірів?2

3. ЗАПИШИ ЦИФРАМИШістсот двадцять. Вісім тисяч. Шість тисяч сімсот сорок два. Вісім тисяч дев'ятнадцять Тисяча п'ять Сім тисяч дев'яносто. П'ять тисяч триста чотири620800067428019100570905304

4. ГРА " ВІДКРИЙ ВІКОНЕЧКО"ЗМЕНШУВАНЕ140170018001300 ВІД'ЄМНИК 501500 900 600 РІЗНИЦЯ 90200 900 700

875* 6 = 5250 72450: 7 = 10350376* 2 = 75 2 286 + 325 = 611537 * 4 = 21548 741 : 3 = 247285 : 3 = 95 6 000+15 = 6 01510 348- 5 728= 4 620 1000 - 611 = 389

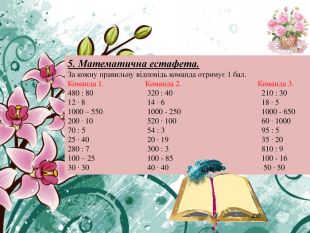
5. Математична естафета. За кожну правильну відповідь команда отримує 1 бал. Команда 1. Команда 2. Команда 3.480 : 80 320 : 40 210 : 3012 ∙ 8 14 ∙ 6 18 ∙ 51000 – 550 1000 - 250 1000 - 650200 ∙ 10 520 ∙ 100 60 ∙ 100070 : 5 54 : 3 95 : 525 ∙ 40 20 ∙ 19 35 ∙ 20280 : 7 300 : 3 810 : 9100 – 25 100 - 85 100 - 1630 ∙ 30 40 ∙ 40 50 ∙ 50

ІV. Робота над темою. Математичний КВК.1. «Кращий математик». Біля дошки працюють по одному представнику від кожної команди, решта – в зошитах. За правильну відповідь – 2 бали. Знайдіть і виправте помилку. Команда 12571 177213× 6 × 415336 794852 Команда 243921 271463× 3 × 4120663 1075952 Команда 331457 51723× 4 × 5125608 25751515 426708 852131 7631085852125 828258 615

2. Знайдіть значення виразу. Команда 1(36 410 + 289 045) ∙ 7 Команда 2(924 301 – 97 038) ∙ 8 Команда 3(278 406 – 238 961) ∙ 6= 2278185= 6618104= 236670

3. Обчисліть значення виразу. (За правильну відповідь – 2 бали)Команда 1а + а ∙ 5, якщо а = 2752 Команда 2b ∙ 3 – b, якщо b = 16588 Команда 3с ∙ 4 + с, якщо с = 5382 Конкурс капітанів.151233 17626 670

4. Конкурс кмітливих. Який добуток більший і на скільки? (За правильну відповідь – 2 бали)Команда 14975 ∙ 3 чи 4463 ∙ 3 Команда 22184 ∙ 4 чи 2774 ∙ 4 Команда 38274 ∙ 5 чи 8247 ∙ 5

V. Домашнє завдання. Кожна з команд направляє представника, який задає заздалегідь приготовлені (можна з допомогою вчителя) задачі з логічним навантаженням. (За правильну відповідь – 3 бали)Команда 1 Матері й синові разом 43 роки, а матері й доньці – 39. Вік обох дітей у сумі складає 16 років. Скільки років матері?Команда 2 Червона Шапочка несла бабусі 14 пиріжків із м’ясом, грибами і капустою. Пиріжків із капустою було найбільше. Їх було вдвічі більше, ніж пиріжків із м’ясом. А пиріжків із м’ясом було більше, ніж із грибами. Скільки пиріжків із грибами несла Червона Шапочка?Команда 3 Маса коробки із зефіром 650 г. Після того як з’їли половину зефіру, маса коробки стала 400 г. Якою є маса порожньої коробки?

Розв’язування: Команда 1. 1) (39 + 43) – 16 = 82 – 16 = 66 (р.) – подвоєні роки матері;2) 66 · 2 = 33 (р.)Відповідь: матері 33 роки. Команда 2.1) На пиріжки з капустою і м’ясом припадає 3 частини, тому виберемо число 12, яке ділиться на 3.2) 12 : 3 – 4 (п.) – з м’ясом;3) 4 · 2 = 8 (п.) – з капустою;4) 15 – 12 = 2 (п.) – з грибами. Відповідь: 2 пиріжки з грибами несла Червона Шапочка. Команда 3.650 – 400 = 250 (г) – маса половини зефіру;2) 250 · 2 = 500 (г) – маса всього зефіру;3) 650 – 500 = 150 (г)Відповідь: 150 г маса порожньої коробки.

V. Підсумок уроку. Підрахунок балів. Нагородження переможців.