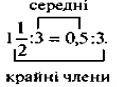Пропорція, члени пропорції. Основні властивості пропорції

Тема.  Пропорція, члени пропорції. Основні властивості пропорції

Мета: сформувати уявлення учнів про зміст понять пропорція, чле­ни пропорції, основна властивість пропорції та виробити вміння засто­совувати ці поняття під час розв'язування типових завдань, що передба­чають їх застосування.

Тип уроку: засвоєння знань, умінь, навичок.

Хід уроку

І. Перевірка домашнього завдання. Актуалізація опорних знань

 Оскільки вправи домашнього завдання мали суто репродуктив­ний характер, правильність їх виконання перевіряємо тільки у «слабких» учнів (взявши зошити під час перерви або під час ви­конання математичного диктанту). Фронтально проводимо математичний диктант (два учні працюють біля дошки. Можна про­вести його у формі самостійної роботи або скласти подібні завдання   тестового  характеру,   передбачивши   у  варіантах відповідей типові помилки.)

Завдання для математичного диктанту

Варіант 1 [2]

1. Чому дорівнює відношення чисел 20 і 4 [ 10 і 2]?
2. Відношення якого числа до числа 7 дорівнює 3 [4]?
3. Відношення числа 18 до числа а дорівнює 3 [ 12 до числа b дорівнює 6].
   Чому дорівнює число а [b].
4. Скоротіть відношення: 10 т до 1 кг [5 хв до 1 год]. Виразіть його у від­сотках.

 Під час аналізу виконання завдань, який проводимо безпосеред­ньо після завершення математичного диктанту, повторюються основні означення і властивості, що були вивчені на попередньо­му уроці.

II. Засвоєння знань

1. Мотивація пізнавальної діяльності

Задача. Одного разу вчені знайшли в Індії давній математичний ру­копис, після розшифровки якого їх зацікавив такий запис:

Як ви думаєте, що він означає?

2. Засвоєння знань учнів

 Формування уявлень учнів про основні поняття теми проводимо традиційно за планом:

1. Поняття пропорції. Приклади пропорцій. Способи запису і читання пропорцій.
2. Елементи пропорції.
3. Основні властивості пропорції.
4. Використання основної властивості пропорції.

Але досі не розв'язане спірне питання: чи бувають пропорції правильними (неправильними) і, відповідно, як формулювати основну властивість пропорції (чи слід вживати термін «правильна пропорція»?). Тому автор на свій розсуд пропонує виробити єдиний підхід до цього питання, а саме: вважати пропорцією будь-яку рівність двох відношень (або рівність, що можна записати в такому вигляді), і тоді, відповідно, розглянути поняття «істинної» пропорції і основну властивість про­порції формулювати, спираючись на поняття істинної пропорції.

Основні теоретичні моменти і записи учнів у зошитах можуть мати вигляд конспекту 23.

III. Засвоєння вмінь

 Основні вміння, над формуванням яких треба попрацювати на цьому уроці, — це:

1. уміння правильно читати пропорції; називати крайні і середні члени пропорції;
2. використовувати основну властивість пропорції, перевіряти істинність записаних пропорцій та складати нові пропорції, спираю­чись на дану істинну пропорцію.

І рівень

Усні вправи

1. Прочитайте пропорції. Чи істинні ці пропорції?

а) 5 : 2= 10 : 4; б) 8 : 2 = 24 : 6; в) = ; г) = .

2. Назвіть крайні та середні члени пропорції:

а) 1 : 2 = 5 : 10; б) 21: 3 = 14 : 2; в) = .

Які рівності випливають із цих пропорцій відповідно до основної властивості пропорції?

ІІ, IIIрівні

Письмові вправи

1. Запишіть пропорцію:

а) 5 так відноситься до 3, як 2 до 1,2;

б) 0,9 так відноситься до , як 45 до 16;

в) відношення до 0,1 дорівнює відношенню 14 до 4,9.

2. Чи істинна пропорція (перевірити двома способами)?

а) 24 : 30 = 28 : 35; б) 2,5 : 2 = 40 : 32; в) 2,1 : 0, 7 = 1,5 : 0,5; г) 1:= 2 : 1.

3. Переставивши крайні або середні числа заданої пропорції, складіть
   три нові істинні пропорції:

а) 6 : 4 = 15 : 10; б) 3: 1,2 = 2,5 : 1; в) =.

4. Пропорція 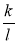= 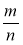істинна. Переставивши її крайні і (або) середні чле­ни, складіть нові істинні пропорції.
5. Виходячи із правильної рівності 12 · 4 = 0,5 · 96, складіть 4 істинних
   пропорцій.
6. Додатково (для кмітливих). Серед чисел 6; 9; 10; 12; 15 виберіть такі,
   щоб із них скласти істинну пропорцію.

IV. Підсумок уроку

Повертаючись до задачі (див. п. II. 1), з'ясовуємо, що означає запис, повторюємо зміст вивчених понять.

V. Домашнє завдання

1. Прочитайте пропорції. Чи істинні ці пропорції?

а) 5 : 2 = 10 : 4; б) 8 : 2 = 24 : 6; в) =; г) =.

2. Назвіть крайні та середні члени пропорції:
   а) 1 : 2 = 5: 10; б) 21 : 3 = 14 : 2; в) =.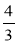
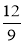3. Чи істина пропорція:

а) 9 : 27 = 3 : 12; б) 3,5 : 0,5 = 21 : 3; в) 35 : 1,5 = 2 : 0,06; г) 2:= 4 : 1?

4. а) Виходячи із правильної пропорції 18 : 5 = 90 : 25, складіть три нові
   істинні пропорції.

б) Виходячи із правильної рівності 6 · 30 = 5 · 36, складіть чотири
істинні пропорції.

5. Обчисліть зручним способом 6,85 · 3,2 – 6,85 · 1,7 + 1,5 · 4,15.