Річна контрольна робота з алгебри та геометрії для 9 класу

Річна контрольна робота з алгебри та геометрії

для 9 класу

1. Розв’яжіть нерівність 9 – х ≥ 2х.

А) (-∞;3];  Б) [3;+∞);B) (-∞;-3];   Г) [-3;+∞).

2.  Обчисліть суму шести перших членів арифметичної прогресії, перший член якої дорівнює -3,5, а різниця 0,4.

А) -15; Б) 15; В) -4,5; Г) 4,5.

3. Центр кола (х+ 4)² + (у- 6)² = 9 має координати…

А) (4;-6), Б) (-4;6), В) (-4;-6), Г) (4;6).

4.  Знайдіть координату х за умови, що вектори і колінеарні, якщо (-2;3) і (х;9).         А) 6, Б) -6, В) 1,  Г) 0.

5. (За кожну відповідність 0,5 б). Установіть відповідність між поданими функціями (1-4) і їх графіками (А-Д).

1) у = (х – 3)²; 2) у = х²-3; 3) у = (х+3)²; 4) у = -х²+3.

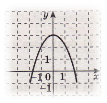
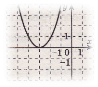
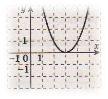
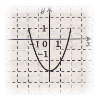А)                     Б)                     В)                    Г)                     Д)

6. Установіть відповідність між фігурами (1-4) і радіусами вписаного в них кола (А-Д).

7. Розв’яжіть нерівність (2х - 7)(2х + 7) ≥ 6х - 51.

8 . Знайдіть координати точок перетину кола х² + у² = 10 і прямої у = х - 2.

9  Знайти суму п’яти перших членів геометричної прогресії (b_n), якщо b₅=16, b₈= 1024.

10.Знайти область визначення функції .

11  Площа ромба дорівнює 600 см², а довжина кола, вписаного в нього, дорівнює 24π см. Обчисліть меншу діагональ ромба.