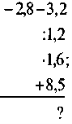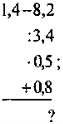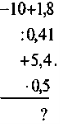Рівняння. Основна властивість рівняння.

Тема. Рівняння. Основна властивість рівняння.

Мета: повторити та узагальнити знання учнів про зміст поняття «рівняння» та пов'язаних з ним понять і способи розв'язання рівнянь, що відомі учням з початкової школи та 5 класу; сформувати уявлення про основні види рівносильних перетворень лінійних рівнянь з однією змінною (на інтуїтивному рівні); розпочати роботу з вироблення вмінь виконувати основні рівносильні перетворення рівнянь для їх розв'я­зування.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний момент

II. Актуалізація опорних знань

Усні вправи

1. Обчисліть:

2. Використовуючи  правила знаходження  невідомих компонентів
   арифметичних дій, розв'яжіть рівняння (знайдіть корінь рівняння):
   а) х - 2,2 = -0,8;   б) х + 2,2 = -0,8;   в) х · (-2,2) = -0,8;

г) х : (-2,2) = -0,8;  д) -2,2 : х = -0,8;   е) -2,2 - х = -0,8;

ж) (х - 3)(х - 2) = 0.

3. Спростіть вираз: a) 5a - 7a + 8b - 2b; б) 3х - 4у – х – у; в) х - (2х - 1);

г) –(х + 1) + (х - 1); д) -2(а - 3); г) -0,2(-2а + 0,3).

III. Мотивація навчальної діяльності

 Задача. На одній шальці терезів лежать два однакових бруски мила, на іншій один такий брусок та ще гирка масою 100 г. Скільки важить один брусок мила?

Розв'язання. Зрозуміло, що один брусок важить 100 г. Але якщо запи­сати рівняння, що відповідає умові задачі, прийнявши масу бруска мила за х (г), будемо мати: 2х = х + 100 — бачимо, що невідоме знаходиться в різних частинах рівняння. Такі рівняння ми поки що розв'язувати не вміємо. Отже, треба дізнатись про певну властивість, яка допоможе нам розв'язати рівняння, що мають невідомі в різних частинах рівняння (вчитель повідомляє тему уроку).

IV. Повторення та систематизація знань

 Перш ніж розібрати з учнями основні види рівносильних перетворень рівнянь, бажано повторити та систематизувати знання про рівняння, які учні повинні мати на цей час, а саме:

• зміст поняття «рівняння» (рівність, в якій є невідоме число);
• корінь рівняння (значення змінної, яке перетворює рівняння на правильну рівність);
• що означає «розв'язати рівняння» (знайти всі корені або довести, що їх немає);
• які правила ми використовували до цього моменту під час розв'язування
  рівнянь (залежності між компонентами  арифметичних дій  та властивість нуля при множенні).

V. Формування знань

  Після проведеного повторення та систематизації знань учнів ми на інтуїтивному рівні формуємо уявлення про основні види рівно­сильних перетворень рівнянь. Формувати такі уявлення можна за допомогою використання наочно-предметних засобів, зокрема уявлення про терези, що в рівновазі (якщо на обидві шальки тере­зів, що перебувають у рівновазі, покласти гирки однакової маси або з обох шальок таких терезів прибрати гирки однакової маси, то терези залишаться в рівновазі).

Таким чином формуємо уявлення про першу властивість рівнянь:

Корені рівняння не зміняться, якщо будь-який доданок (доданки) перенести з однієї частини рівняння в іншу, змінивши при цьому його знак (на про­тилежний).

І якщо сам цей висновок для більшості учнів зрозумілий, то його за­стосування потребує копіткої роботи.

VI. Закріплення знань. Вироблення вмінь

Усні вправи

1. Чи правильно виконано перенесення доданків з однієї частини в іншу
   в рівнянні: 2х - 3 = х - 7?

а) 2х – 3 – х – 7 = 0; б) 2х – х = -7 - 3; в) -2х + х = -7 + 3; г) 2х – х = 7 + 3.

2. Поясніть кожний крок розв'язування рівняння:

7х - 14 = 5х;  7х - 5х = 14; 2х = 14; х = 14 : 2; х = 7.

Письмові вправи

 Перед розв'язуванням письмових вправ слід ще раз пояснити, що переносити з однієї частини рівняння в іншу можна тільки додан­ки; переносять доданки так, щоб в одній частині рівняння були відомі числа, а в іншій — невідомі.

1. Перенесіть із лівої частини рівняння в праву доданок, що не містить
   невідомого: а) -5х + 1,2 = 2х + 11; б) 4х – 9 = -х - 5,2.
2. Перенесіть у ліву частину рівняння всі доданки, що містять невідоме, а в пра­ву, що не містять невідомого: а) 17х - 5 = 8х + 5,6; б) -11у + 7 = -3у - 10.
3. Розв'яжіть рівняння:

а) 7х - 5 = 6х + 1;  б) 4х - 3 = 2х + 5;   в) 9 - 8у = -6у + 1;

г) 6m + 3 = 7m + 8;  д) -9m – 2 = 9m - 2;  е) -9а + 6 = -10а + 15;

ж) 4у + 7 = -5 + 4у;  з) 0,7х + 1,6 = -0,1х;  к) -4,5х - 3 = 2,7х + 15;

л) 39 - 7у + 17 = 3y + 16;  м) 15 – 6х = 2х - 5х - 3.

 (Перш ніж переносити доданки, треба спростити вирази в правій та лівій частинах окремо (звести подібні доданки, якщо вони є).

Логічна задача

4. Знайдіть пропущене число:

VI. Підсумки уроку

Сформулюйте правило переносу доданків з однієї частини рівняння в іншу. Чи однакові корені мають рівняння 2х - 3 = х + 5 та 2х – х = 5 - 3? Чому?

VII. Домашнє завдання

1. Розв'яжіть рівняння:

а) 5х - 5 = 2х - 7;   б) х – 9 = 3х - 6;   в) 4,5у + 1 = -5 + 5у;

г) 11х - 1,8 = 7х + 1,4;  д) 5,6х – 1 = -1 + 6х;  e) 5,7m - 13,75 = 8,2m.

2. Спростіть вираз:

а) 5m - (3m + 5) + (2m - 4);  б) -5(х + 3) + 4(х – 2) – 6(2х + 1);

в) 0,2(6х - 5) - 4(0,2х - 2);  г) 0,4(1,5y + 3) -2,5(3 - 0,6y);

д) ;   е) .

3. Задача. До деякого числа додали 62, здобуту суму помножили на 3 і дістали 32. Знайдіть невідоме число.