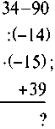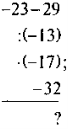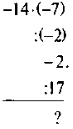Рівняння. Основна властивість рівняння

Тема. Рівняння. Основна властивість рівняння

Мета: продовжити роботу з вироблення вмінь правильно переносити доданки з однієї частини рівняння в іншу; сформувати уявлення про дру­гу основну властивість рівнянь та розпочати роботу з вироблення вмінь використовувати множення або ділення обох частин рівняння на одне й те саме число, відмінне від 0, для розв'язування рівнянь.

Тип уроку: засвоєння знань, умінь, навичок.

Хід уроку

I. Організаційний момент

II. Перевірка домашнього завдання

Два-три учні працюють біля дошки: з карток з відповідями, які вчи­тель заготував заздалегідь, вибирають відповіді, які вважають правиль­ними до вправ домашнього завдання, які вчитель розподіляє між ними на власний розсуд.

Усні вправи

1. Обчисліть:

2. Зведіть подібні доданки:  а) 3т + 2т + 4т;  б) 3т - 2т + 4т; 

в) 3т + 2т - 4т;  г) 3т - 2т - 4т;  д) -3т - 2т - 4т.

3. Серед рівнянь знайдіть такі, що мають однакові корені (не розв'язу­ючи рівнянь): а) 3х - 4 = х + 5; б) 3х – х = -4 + 5; в) 3х – х = 5 + 4; г) 3 = 9;
   д) 2х = 9; е) 2х = 1; ж) 2х = -1.

III. Актуалізація опорних знань

Усні вправи

1. Розв'яжіть рівняння та порівняйте їх корені: 3(х + 2) = 12; х + 2 = 12 : 3.
2. На яке число можна помножити дані групи чисел, щоб дістати в до­бутках тільки натуральні числа?

а) , 3, 6,5;  б) , ;  в) , ; г) , , , 0,5.

IV. Мотивація навчальної діяльності

 На цьому етапі уроку треба дати зрозуміти учням, що властивості рівнянь, які вони розглянули на попередньому уроці і які розгля­нуть сьогодні, є інструментом, що допомагає спрощувати розв'я­зування рівнянь.

V. Формування знань

 Властивість рівняння, яку автор також пропонує дати учням, є ос­новою для розуміння алгоритмів розв'язування дробових рівнянь (8 кл.) та багатьох лінійних рівнянь (7 кл.), і використання цієї властивості для розв'язування рівнянь, що містять дроби (раціональні або звичайні), з досвіду автора, викликає певні труд­нощі в семи-та восьмикласників. Тому вважаємо за доцільне розпочати роботу з вироблення вмінь застосування цієї властивості рівносильності рівнянь уже в 6 класі.

1. Розв'яжіть рівняння 4(х + 5) = 12.  (1)

Розв'язання. За правилом знаходження невідомого множника, х + 5 = 12.4, тобто х + 5 = 3. Звідси х = 3 - 5, х = -2

2. Розв'яжіть рівняння(4(х + 5)) : 4 = 12 : 4.    (2)

Розв'язання. За властивістю ділення, маємо:

4(х + 5) : 4 = х + 5, 12 : 4 = 3, тому х + 5 - 3, х = 3 - 5, х = 2.

Порівнявши (1) і (2) та їх розв'язання, доходимо висновку:

Корені рівняння не змінюються, якщо його обидві частини помно­жити або поділити на одне й те саме число, що не дорівнює 0.

Приклад. Розв'яжіть рівняння х + 12 = х.

Розв'язання. Помножимо обидві частини рівняння на 3:

х + 12 = х | -3; 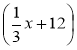·3 = х · 3; х + 36 = 3х або 3х = х + 36.

Далі розв'язуємо рівняння, переносячи невідомі доданки в одну час­тину, а відомі залишаючи в іншій. 3х – х = 36; 2х = 36; х = 18.

Перевірка: ·18 + 12 = 18 — правильна рівність.

Отже, якщо рівняння містить дробові коефіцієнти, можна позбутися цих дробів, помноживши праву та ліву частини рівняння на знаменник (спільний) цих дробових коефіцієнтів.

VI. Закріплення знань. Вироблення вмінь

Усні вправи

1. На яке число можна поділити праву та ліву частини рівняння, щоб
   дістати рівняння із цілочисленими коефіцієнтами?

а) х + 6 = 7; б) х + 6 = -х + 1; в) х + 6 = х + 1; г) х + = х - 1.

2. Виконайте множення: 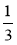х · 3; 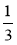х · 6; ; .

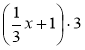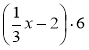Письмові вправи

1. Виконавши множення обох частин рівняння на одне й те саме число,
   позбудьтеся дробових чисел та розв'яжіть рівняння:

а) х – 4 = -х + 1; б) -2- 3х = -1х; в) х + 3 = х + 2;

г) х + 3 = х + 5; д) у - у + 2 = у - 3; є) х + х + 5 = х;

ж) 0,2х + 2,3 = 0,7х - 3,2.

2. Поділивши обидві частини рівняння на одне й те саме число, що не
   дорівнює 0, розв'яжіть рівняння:

а) -40 · (-7х + 5) = -1600; б) (-20х - 50) · 2 = 100; в) 2,1 · (4 - 6у) = - 42;

г) -3 · (2 – 15х) = -6.

Вправи на повторення

3. При якому значенні а значення виразів -3а + 11 та 7а - 1 рівні?
4. Логічна вправа додатково
   Знайдіть пропущене число:

VII. Підсумки уроку

1. Обидві частини рівняння помножили на -3; 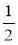. Чи змінились корені рівняння?
2. Обидві частини рівняння поділили на -0,3; 2. Чи змінились корені
   рівняння?

VIII. Домашнє завдання

1. Розв'яжіть рівняння:

а) 2 - х = - х + 3; б) х - 2 = -х;  в) 1х + = -х + 2;

г) у - = ; д) х + х – 1 = 1.

2. Розв'яжіть рівняння (поділивши праву та ліву частину рівняння) та
   виконайте перевірку.

а) -20 · (х - 13) = -220;  б) (30 - 7х) · 8 = 352;  в) (2,8 - 0,1х) · 3,7 = 7,4;

г) (3х - 1,2) · 7 = 10,5.

3. Розкрийте дужки та зведіть подібні доданки: а)3(у – 5) – 2(у – 4);

б) -5(5 – х) – 4х; в) (3х – 6) – (7х – 21); г) 5,4(3у – 2) – 7,2(2у – 3);

д) (1,8m – 5,4) – (2,1m – 4,2); є) (0,3y – 0,6) – (0,4у – 0,8).